论文题目：Adding Conditional Control to Text-to-Image Diffusion Models

发表会议：International Conference on Computer Vision(ICCV 2023, Best Paper(Marr Prize))

第一作者：Lvmin Zhang(PhD with Stanford University)

Question

如何在 Text-to-Image Diffusion 图像生成模型中添加条件控制其图像的生成(这里的条件主要包括 visual condition，如 mask, depth等，即输入的条件也是图像)，同时保证其生成图像的逼真性。

Preliminary

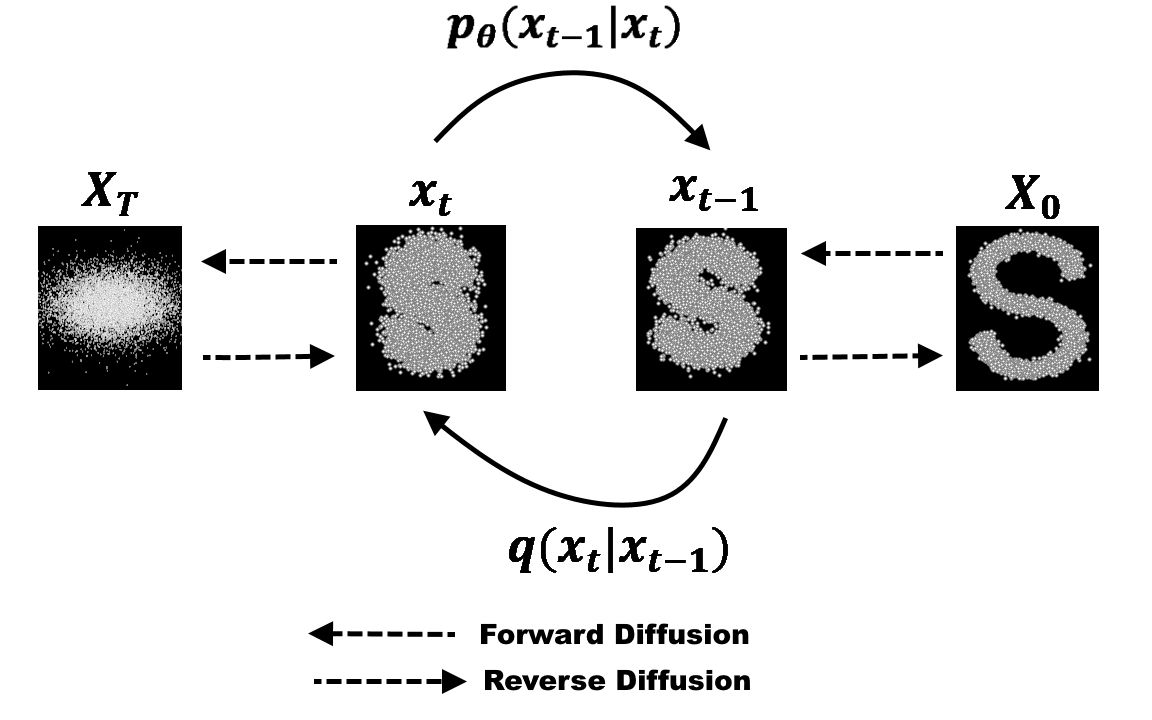
Diffusion Model：扩散模型是近年来最热的图像生成思想。 将任意一张图像 $I_0$ 进行噪声添加，每次添加一个服从 $N(0,1)$ 分布的随机噪声 $\epsilon_t$，获得含有噪声的图像 $I_t$，则进行了无数次后，原本的图像就会变成一个各向同性的随机高斯噪声。 按照这个理论，我们对一个各向同性的随机高斯噪声每次添加一个特定的服从 $N(0,1)$ 分布的噪声 $\epsilon_t'$，获得噪声量减少的图像 $I_t'$，则经过足够多次后便可获得一张逼真的图像 $I_0'$。 为此，我们可以选择任意一个图像生成模型 $M_G$ (例如 U-net 等)，第 t 次时输入第 t-1 次生成的图像 $I_{t-1}'$，输出生成的图像 $I_t'$。 由于每次使用的是同一个图像生成模型 $M_G$，所以需要输入时间步信息 $t$ 来告诉模型现在是生成的第几步 (一个直观的理解是在随机噪声恢复成原始图像的前期，模型更关注图像的整体恢复，而后期则更加关注图像的细节恢复，所以需要时间步信息告诉模型现在是偏前期还是后期)。 同时通过 $I_{t-1}$ 直接生成 $I_t$ 较为困难，因为它需要生成正确其每个像素值，而每次添加的噪声 $\epsilon_t$ 较容易预测。 因此可以更换为每次输入 $I_{t-1}$，模型预测第 $t$ 次所加的噪声 $\epsilon_t$。所以损失函数为 $L = E_{z_0, t, c_t, \epsilon \sim N(0,1)}[||\epsilon - \epsilon_{\theta}(z_t, t, c_t)||_2^2]$。 其中 $z_0$ 是原始噪声(即一开始输入的图像)，而 $z_t$ 是第 $t$ 步输出的图像, $\epsilon_{\theta}(z_t, t, c_t)$ 为模型预测的第 $t$ 步所加的噪声。

Method

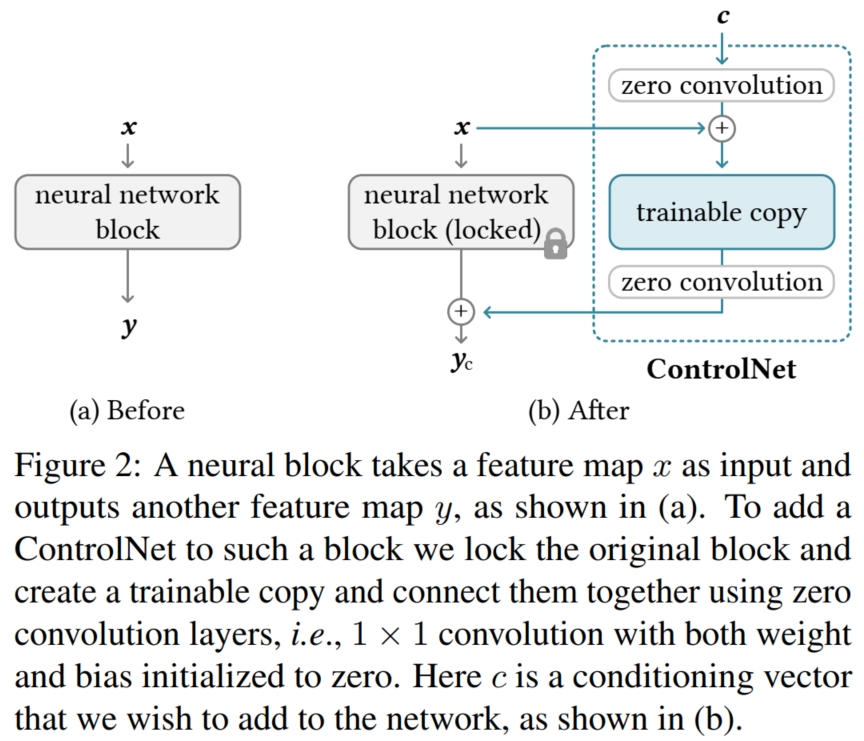
这个问题最简单的方法是找到一个带有该条件(假设为 $C_i$)的数据集，再在别人已经预训练好的 Difussion 模型上进行微调。 但是这么做有一个问题：因为预训练的 Diffusion Model 是在大量图像上训练而来，如果直接将整个模型直接进行有监督微调，可能会使得模型生成效果大打折扣(即文中说的 overfitting 和 catastrophic forgetting)。 所以本文解决的是在加入了条件 $C_i$ 的情况下，既能输出符合条件 $C_i$ 的图像，又能保证其逼真度；同时，本文还解决了多个 $C_i$ 同时作用于一张图像的生成问题，并且训练的参数也较少。 本文的方法较为简单，可以看作是一个即插即用的插件模块。如图，对于任意一个 Diffusion 模型，它通常是由每个基本单元块 $net_{b}$ 组成(如 resnet block, transformer block等)。 原始的 Diffusion 模型输入上一次 $net_{b}$ 生成的 feature map $x$，输出更新的 feature map $y$。 而 ControlNet 保持每个 $net_b$ 的参数不动(即 freeze parameter)，并复制出一个相同的 $net_b'$，称为 $trainable\ copy$，作为条件 $C_i$ 的处理模块。 并在 $trainable\ copy$ 前后都添加了额外的模块 $zero\ convolution$：它是一个卷积层，其卷积核权重和偏置都初始化为 0。 设 $net_b$ 的数学函数为 $\digamma(x;\Theta)$，$zero\ convolution$ 的数学函数为 $Z(·;·)$， 则 ControlNet 的输入输出公式为 $y_c = \digamma(x;\Theta) + Z(\digamma(x + Z(c;\Theta_{z1});\Theta_c); \Theta_{z2})$。 由于 $zero\ convolution$ 的参数初始化为 0，所以 $Z(c;\Theta_{z1}) = 0$， $\digamma(x + Z(c;\Theta_{z1});\Theta_c) = \digamma(x;\Theta_c)$，则 $trainable\ copy$ 在开始时依旧接收 $x$ 作为输入，和无条件训练的情况一致。 这样可以极大程度保持原始预训练模型的 capability。 同时 $Z(\digamma(x + Z(c;\Theta_{z1});\Theta_c); \Theta_{z2}) = 0$， 所以 $y_c = \digamma(x;\Theta) + Z(\digamma(x + Z(c;\Theta_{z1});\Theta_c); \Theta_{z2}) = \digamma(x;\Theta)$。 这样，在训练刚开始时，有害噪声就不会影响 $trainable\ copy$ 中神经网络层的隐藏状态。 而训练损失函数则和普通的 Diffusion Model 类似：假设 time step 为 $t$(Diffusion 模型训练的时间步), text prompts 为 $c_t$(文本条件), visual condition 为 $c_f$(即我们自己添加的额外条件)，训练模型为 $\epsilon_{\theta}$， 则损失函数为 $L = E_{z_0, t, c_t, c_f, \epsilon \sim N(0,1)}[||\epsilon - \epsilon_{\theta}(z_t, t, c_t, c_f)||_2^2]$。 其中 $z_0$ 是原始噪声(即一开始输入的图像)，而 $z_t$ 是第 $t$ 步输出的图像。

对于多个条件 $c_1,...,c_n$，本文采用最直接的方式，直接将每个条件 $c_i$ 对应的 ControlNet 的输出相加， 即 $y_c = \sum_{i=1}^n{y_{c_i}}$。 没有任何额外的权重或线性插值。