论文题目：HumanMAC: Masked Motion Completion for Human Motion Prediction

发表会议：International Conference on Computer Vision(ICCV 2023)

第一作者：Ling-Hao Chen(Tsinghua University)

共同一作：Jiawei Zhang(Xidian University Undergraduate)；我同学，非常有实力的一个人，本科就发表了 2 篇 B 类的论文和 1 篇 ICCV 顶会论文

Question

如何使用尽可能少的 loss 函数和 train stage 来完成 human motion prediction(HMP) 任务，同时还要使得模型能够实现不同 motion 类型之间的自然过渡(switch)。

Preliminary

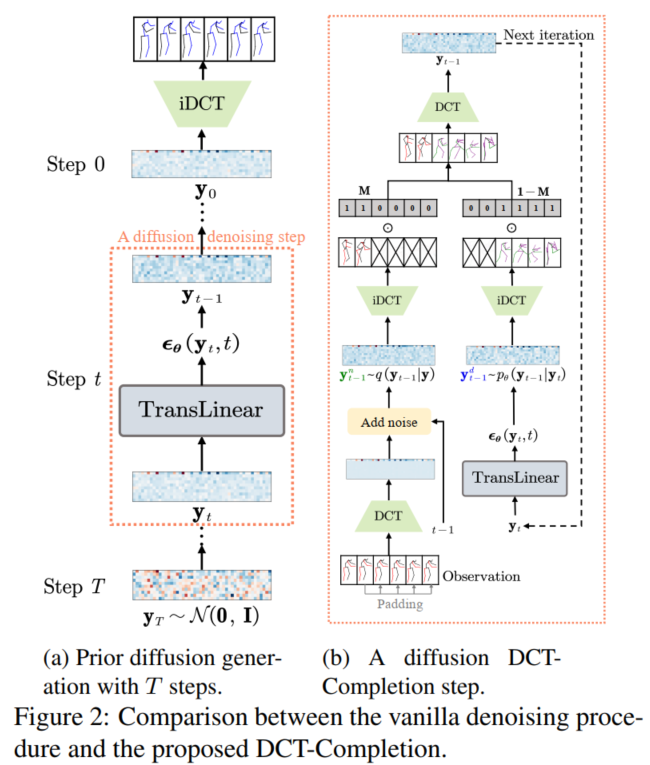
Diffusion Model(DM)：扩散模型是近年来最热的图像生成思想。如图 1 (a), 将任意一张图像 $I_0$ 进行噪声添加，每次添加一个服从 $N(0,1)$ 分布的随机噪声 $\epsilon_t$，获得含有噪声的图像 $I_t$，则进行了无数次后，原本的图像就会变成一个各向同性的随机高斯噪声。 按照这个理论，我们对一个各向同性的随机高斯噪声每次添加一个特定的服从 $N(0,1)$ 分布的噪声 $\epsilon_t'$，获得噪声量减少的图像 $I_t'$，则经过足够多次后便可获得一张逼真的图像 $I_0'$。 为此，我们可以选择任意一个图像生成模型 $M_G$ (例如 U-net 等)，第 t 次时输入第 t-1 次生成的图像 $I_{t-1}'$，输出生成的图像 $I_t'$。 由于每次使用的是同一个图像生成模型 $M_G$，所以需要输入时间步信息 $t$ 来告诉模型现在是生成的第几步 (一个直观的理解是在随机噪声恢复成原始图像的前期，模型更关注图像的整体恢复，而后期则更加关注图像的细节恢复，所以需要时间步信息告诉模型现在是偏前期还是后期)。 同时通过 $I_{t-1}$ 直接生成 $I_t$ 较为困难，因为它需要生成正确其每个像素值，而每次添加的噪声 $\epsilon_t$ 较容易预测。 因此可以更换为每次输入 $I_{t-1}$，模型预测第 $t$ 次所加的噪声 $\epsilon_t$。所以损失函数为 $L = E_{z_0, t, c_t, \epsilon \sim N(0,1)}[||\epsilon - \epsilon_{\theta}(z_t, t, c_t)||_2^2]$。 其中 $z_0$ 是原始噪声(即一开始输入的图像)，而 $z_t$ 是第 $t$ 步输出的图像, $\epsilon_{\theta}(z_t, t, c_t)$ 为模型预测的第 $t$ 步所加的噪声。

Method

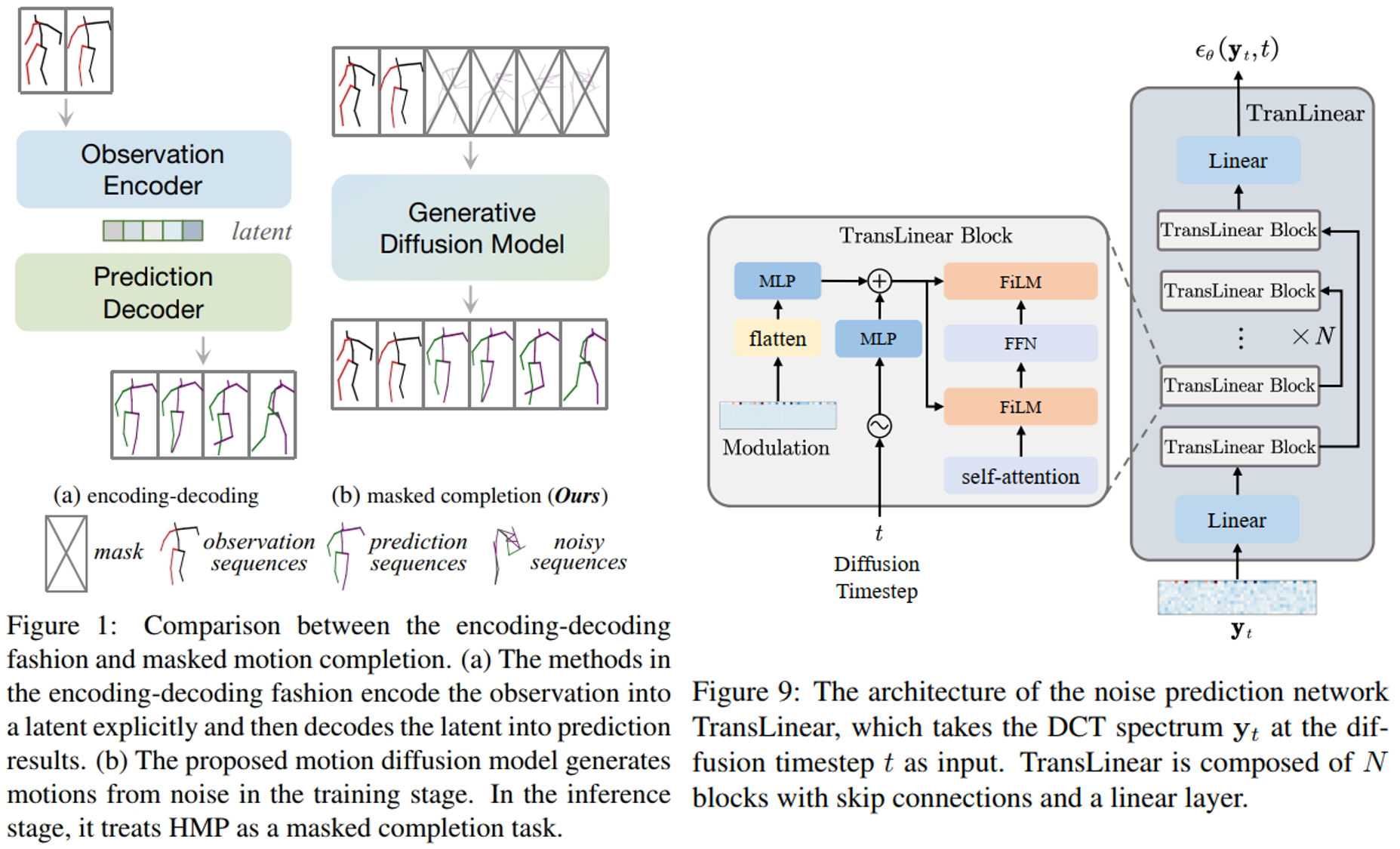
如图 2 (a), 在此之前，解决 HMP 的主流方法都是使用 encoder-decoder 架构，即使用 encoder 对已观测到的 motions 进行编码获得 latent， 再使用 decoder 对 latent 进行解码获得剩下的预测 motions，但是这种方法有 $3$ 个弊端： 1) 它们通常都是使用 multi-loss 限制模型训练，这样就需要设计 hyper-parameter 来平衡各个损失； 2) 大多方法也需要 multi-stage training，这也增加了 tuning 的困难； 3) 这类方法很难实现不同 motion 类型之间的自然过渡，因为这些方法都是在大量受限的已观测数据上进行预测，而已观测数据中很少存在 switch (其实我对第三点不理解，之前的模型虽然只是将已观测数据作为输入，但是它们的目标是预测出未观测数据，它们整个组合起来就是 switch，在模型学习中肯定或多或少都能关注到 switch。 我觉得换成它们没有显式地建模 switch 会更好)。 为此，本文放弃了 encoder-decoder 架构，使用新的角度来看待整个问题： 如果将未被观测到的 motions 看作是被 mask 的，那就是一个掩码补全问题(masked motion completion framwork)。

• 具体而言， 假设已观测到的 motions 为 $x^{(1:H)} = [x^{(1)};...;x^{(H)}] \in R^{H \times 3J}$ 表示 $H$ 帧，每帧 $J$ 个关节(joint)的 $3$ 维坐标。 HMP 需要预测接下来的 $F$ 帧 motions $x^{(H+1:H+F)} = [x^{(H+1)};...;x^{(H+F)}] \in R^{F \times 3J}$。 在 training 时，本文使用传统的 $DM$ 模型，将已观测到的数据和需要预测的数据看作一个整体 $x^{(1:H+F)}$ 进行正常的去噪训练。 首先将 $x^{(1:H+F)}$ 使用离散余弦变换 $DCT$ 转换到频域 $y = DCT(x) = Dx, D \in R^{(H+F) \times (H+F)}$，其中 $D$ 是预定义的 $DCT$ basis。 由于 $DCT$ 是正交变换，最后只需要通过反离散余弦变换 $iDCT$ 将结果 $\hat{y}$ 转换回时间域即可：$\hat{x} = $iDCT$(\hat{y}) = D^T\hat{y}$。 在本文中，为了减少计算量并去除高频部分(通常高频部分是噪声或者难以察觉的细节)，仅使用前 $L$ 行的 $D$ 进行 $DCT$，即 $y_0 = D_Lx, D_L \in R^{L \times (H+F)}$。 然后对频域的 $y_0$ 使用重参数技巧添加噪声获得带噪数据： $y_t = \sqrt{\bar{\alpha_t}}y_0 + \sqrt{1-\bar{\alpha_t}}\epsilon;\ \bar{\alpha_t} = \prod_{i=1}^t{\alpha_i}, \alpha_i \in [0,1], \epsilon \sim N(0,I)$。 然后使用 $TransLinear$ 模型 $\Theta$ (如图 3) 进行训练，损失函数为 $L = E_{\epsilon, t}[||\epsilon - \epsilon_{\theta}(y_t, t)||^2]$。

• 在 inference 时，由于在训练阶段没有输入额外条件，所以直接使用训练好的 DM 模型进行预测会使得模型生成的 motion 很随机，很可能没有以已观测到的 motions 为前提。 使用需要设计将已观测到的 motions 作为条件来限制模型的输出。本文采用一种十分巧妙的 mask 方法，称为 $DCT-Completion$，这种方法使得模型不需要重新训练就可以进行推理。 具体而言，对于从第 $t$ 步推理到第 $t-1$ 步，模型分成了 $2$ 个分支。 如图 1 (b) 的左边分支，首先对于已观测的 motions $x^{(1:H)}$，将其最后一帧填充到需要预测的帧中，即令 $x^{(H+1)},...,x^{(H+F)} = x^H$， 再对填充得到的 $x$ 进行 $DCT$ 得到 $y$。 接着对 $y$ 中添加时间步为 $t-1$ 的噪声获得含有噪声的 $y_{t-1}^n$，即 $y_{t-1}^n = \sqrt{\bar{\alpha}_{t-1}}y + \sqrt{1 - \bar{\alpha}_{t-1}}z, z \sim N(0, I)$，则可以得到 $y_{t-1}^n \sim q(y_{t-1}|y)$。 同时，如图 1 (b) 的右边分支，模型使用前一步预测得到的 $y_t$ 进行进一步去噪得到 $y_{t-1}^d$：$y_{t-1}^d = \frac{1}{\sqrt{\alpha_t}}(y_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}\epsilon_{\theta}(y_t, t))}+\sigma_tz; z \sim N(0,I)$$\ if\ t = 1\ else\ 0$， 则可以得到 $y_{t-1}^d \sim p_{\theta}(y_{t-1}|y_t)$。 对于 $y_{t-1}^n$，它的前 $H$ 帧是由观测数据加入第 $t-1$ 步噪声得到的，应该更加接近真实数据在第 $t-1$ 步时前 $H$ 帧的值； 而 $y_{t-1}^d$，它的后 $F$ 帧是由模型从第 $t$ 步的输出 $y_t$ 进一步预测得到的，应该更加接近真实数据在第 $t-1$ 步时后 $F$ 帧的值。 所以，我们把 $y_{t-1}^n$ 的前 $H$ 帧和 $y_{t-1}^d$的后 $F$ 帧结合起来，作为本次模型预测得到的输出 $y_{t-1}$。 具体而言，本文使用了 mask $M$ 在时间域上来实现这个操作。 $M = [1_1,...,1_H,0_1,...,0_F]$ 是一个前 $H$ 个为 $1$，后 $F$ 个为 $0$ 的掩码向量，则 $1 - M$ 是一个前 $H$ 个为 $0$，后 $F$ 个为 $1$ 的掩码向量。 通过先将 $y_{t-1}^n$ 和 $y_{t-1}^d$ 使用 $iDCT$ 转换到时间域，在将其乘上各自的掩码，最后再转换回频域，即可获得 $y_{t-1}$： $y_{t-1} = DCT(M \bigodot $iDCT$(y_{t-1}^n) + (1 - M) \bigodot $iDCT$(y_{t-1}^d)$。

最后经过 $T$ 步去噪步骤后，将得到的 $y_0$ 进行 $iDCT$，则其后 $F$ 帧就为模型预测得到的结果。 train 和 inference 算法如下：

针对含有 switch 的数据，本文采用不同的策略进行 inference。 除了提供前 $H$ 观测帧 motions 之外。还提供后 $P$ 目标帧 motions，并将掩码 $M$ 进行修改，设计为 $M = [1_1,...,1_H,0_1,...,0_{F-P},1_1,...,1_P]$。 由于本文在训练时时直接对整个序列进行建模，使得生成的 motions 被限制为在观测($H$)、预测($F_P$)和目标($P$)帧之间连续。 此外，得益于运动的连续性，训练后的模型能够自然地完成不同类别运动的切换。