论文题目：iTransformer: Inverted Transformers Are Effective for Time Series Forecasting

发表会议：截至2023年10月20日暂无，论文版本为 arxiv-v1

第一作者：Yong Liu(Tsinghua University)

Question

如何使用尽可能小的改动解决 Transformer 在 Time Series Forecasting(时间序列预测 TSF) 问题上无法取得高性能的问题

Method

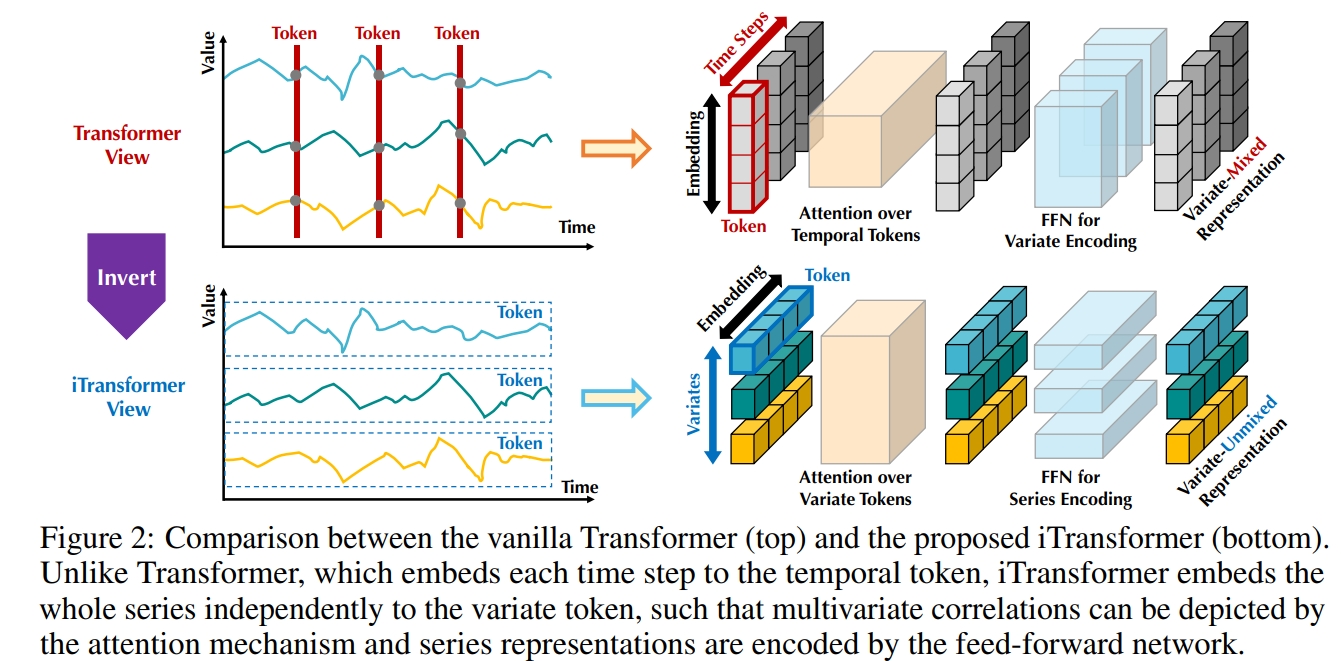
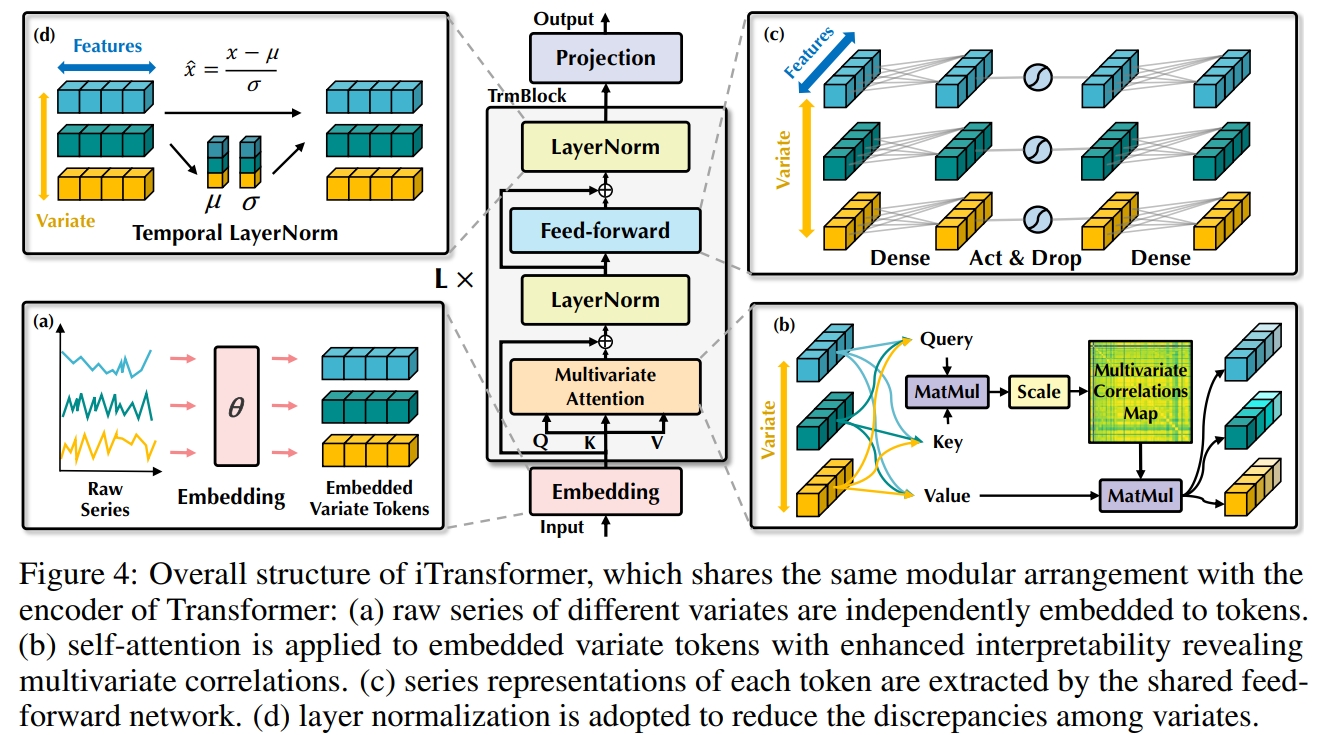
本文通过分析发现 Transformer 架构之所以无法在 TSF 问题上取得高性能不是本身架构问题，而是输入数据的结构不对。 如图 1 的上半部分，之前的方法通常都是将每个时间戳作为一个数据，把时间长度作为序列长度送入 Transformer 进行建模。 然而，同一时间戳中的多个变量之间表示完全不同的物理含义，将这些变量嵌入到一个 token 中，容易消除它们之间的多元相关性。 同时由于现实世界中多变量时间戳的过度局部感受野(即每个 token 只有一个时间戳)和未对齐的时间线(即不同的变量是使用不同的测量方法获得的，同一时间戳的变量值在现实生活中可能不在同一时间)， 单个时间戳的 token 可能很难揭示有用信息。 另外，时间序列变化受序列顺序的影响较大(相同的时间戳序列不同的排列表示不同的时间序列)， 但在时间维度上采用排列不变注意力机制(attention 机制是全局建模，导致数据排序对其不影响)的方法并不恰当。 所以应该更换数据输入进 Transformer 的方式。 具体而言，假设历史观测序列为 $X = \{x_1, ..., x_T\} \in R^{T \times N}$，需要预测未来 $S$ 步时间戳 $Y = \{x_{T+1}, ..., x_{T+S}\} \in R^{S \times N}$。 而 $X_{t,:} \in R^N$ 表示第 $t$ 时间戳的所有变量值组成的向量，$X_{:,n} \in R^T$ 表示第 $n$ 个变量的所有时间戳数据组成的向量。 之间的方法是将 $X_{t,:}$ 作为 token 进行模型学习，而本文是将每个变量作为 token，即将 $X_{:,n}$ 作为 token 进行模型学习。 这种数据输入形式可以使得模型更多关注于多变量序列的表示学习和自适应关联。 而模型主要包括三部分：1) Embedding; 2) TransformerBlock; 3) Projection。

• Embedding：和普通的 Transformer 一致，Embedding 层是一个 MLP， 它将原始数据 $X \in R^{T \times N}$ 映射为潜表示 $H \in R^{D \times N}$：$h_n^0 = Embedding(X_{:,n}), H = \{h_1,...,h_N\}$， 便可将 $H$ 送入模型进行训练。

• Transformer：其架构和普通的 Transformer 一致，包括 LayerNorm，Self-Attention 和 FFN。 不同的是，iTransformer 只有唯一的输入 $H$，而没有加入位置信息，因为各个变量的排序对学习变量间的相关性影响不大。 对于 LayerNorm，模型针对每个 $h_n$ 进行归一化：$LayerNorm(H) = \{\frac{h_n - Mean(h_n)}{\sqrt{Var(h_n)}}\}|n = 1,...,N$。 对于 Self-Attention，模型主要利用注意力机制学习各个变量之间的相关性(即学习不同的 $h_n$ 之间的关联性)， 通过 $W_Q^{l-1},W_K^{l-1},W_V^{l-1} \in R^{D \times d_k}$ 将 $H^{l-1}$ 投射到不同的表示： $Q^{l-1} = HW_Q^{l-1}, K^{l-1} = HW_K^{l-1}, V^{l-1} = HW_V^{l-1}$。 并使用注意力机制计算新的表示：$\hat{H}^l = (Q^{l-1}{K^{l-1}}^T/\sqrt{d_k})V^{l-1}$。 对于FFN：模型主要是为了学习时间序列的复杂表示(即独立学习每个 $h_n$ 的表示)， 因为FFN(MLP)可以通过训练描绘任何时间序列的固有属性，如振幅、周期性，甚至频谱(神经元作为滤波器)，这是比应用于时间戳的自注意力(即之前的方法)更有利的预测表示学习器。 最终，Transformer输出更新的 $H^{l+1}$：$TrmBlock(H^l), l=0,...,L-1$。

• Projection：和 Embedding 一致，Projection 层也是一个 MLP， 它将最终学到的潜变量$H \in R^{D \times N}$ 映射为预测的数据 $\hat{Y} \in R^{S \times N}$： $\hat{Y}_{:,n} = Projection(h_n^L), n = 1,...,N$。