论文题目：Matryoshka Diffusion Models

发表会议：截至2023年10月26日暂无，论文版本为 arxiv-v1

第一作者：Jiatao Gu (Apple)

Question

如何使用一个 end-to-end 架构，实现生成高分辨率的逼真图像($1024 \times 1024$)，同时使用较少的计算量和较为简单的优化函数(即损失)。

Preliminary

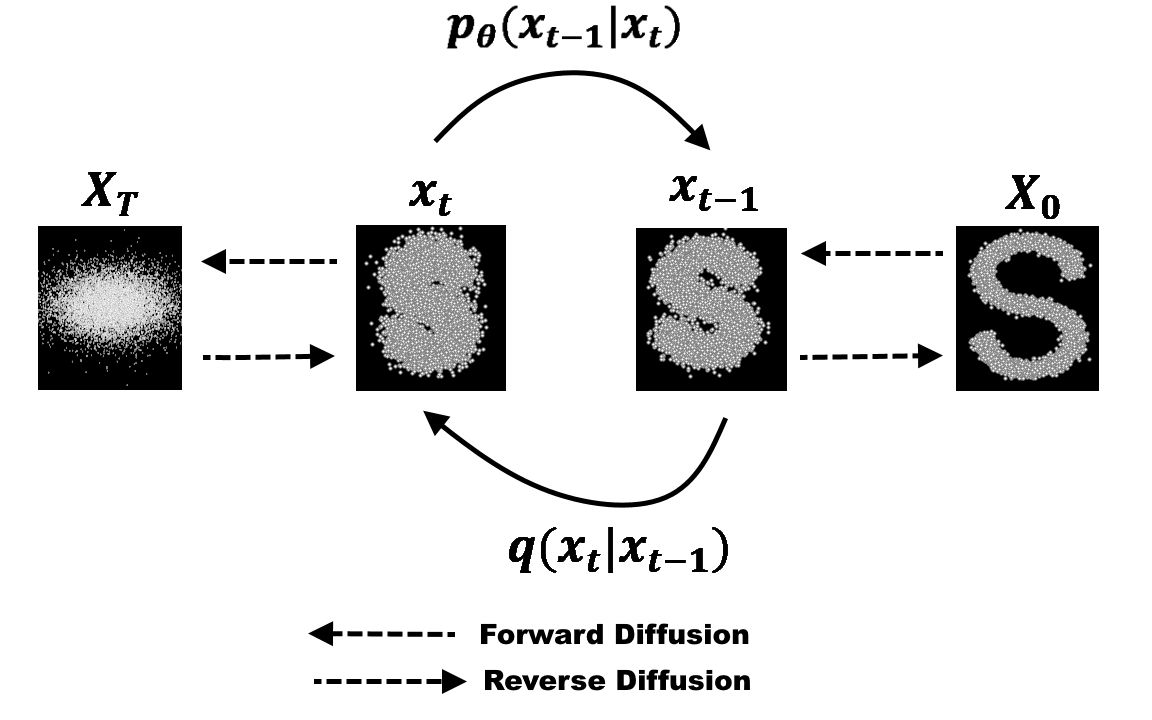
Diffusion Model (DM)：扩散模型是近年来最热的图像生成思想。 将任意一张图像 $I_0$ 进行噪声添加，每次添加一个服从 $N(0,1)$ 分布的随机噪声 $\epsilon_t$，获得含有噪声的图像 $I_t$，则进行了无数次后，原本的图像就会变成一个各向同性的随机高斯噪声。 按照这个理论，我们对一个各向同性的随机高斯噪声每次添加一个特定的服从 $N(0,1)$ 分布的噪声 $\epsilon_t'$，获得噪声量减少的图像 $I_t'$，则经过足够多次后便可获得一张逼真的图像 $I_0'$。 为此，我们可以选择任意一个图像生成模型 $M_G$ (例如 U-net 等)，第 t 次时输入第 t-1 次生成的图像 $I_{t-1}'$，输出生成的图像 $I_t'$。 由于每次使用的是同一个图像生成模型 $M_G$，所以需要输入时间步信息 $t$ 来告诉模型现在是生成的第几步 (一个直观的理解是在随机噪声恢复成原始图像的前期，模型更关注图像的整体恢复，而后期则更加关注图像的细节恢复，所以需要时间步信息告诉模型现在是偏前期还是后期)。 同时通过 $I_{t-1}$ 直接生成 $I_t$ 较为困难，因为它需要生成正确其每个像素值，而每次添加的噪声 $\epsilon_t$ 较容易预测。 因此可以更换为每次输入 $I_{t-1}$，模型预测第 $t$ 次所加的噪声 $\epsilon_t$。所以损失函数为 $L = E_{z_0, t, c_t, \epsilon \sim N(0,1)}[||\epsilon - \epsilon_{\theta}(z_t, t, c_t)||_2^2]$。 其中 $z_0$ 是原始噪声(即一开始输入的图像)，而 $z_t$ 是第 $t$ 步输出的图像, $\epsilon_{\theta}(z_t, t, c_t)$ 为模型预测的第 $t$ 步所加的噪声。

Method

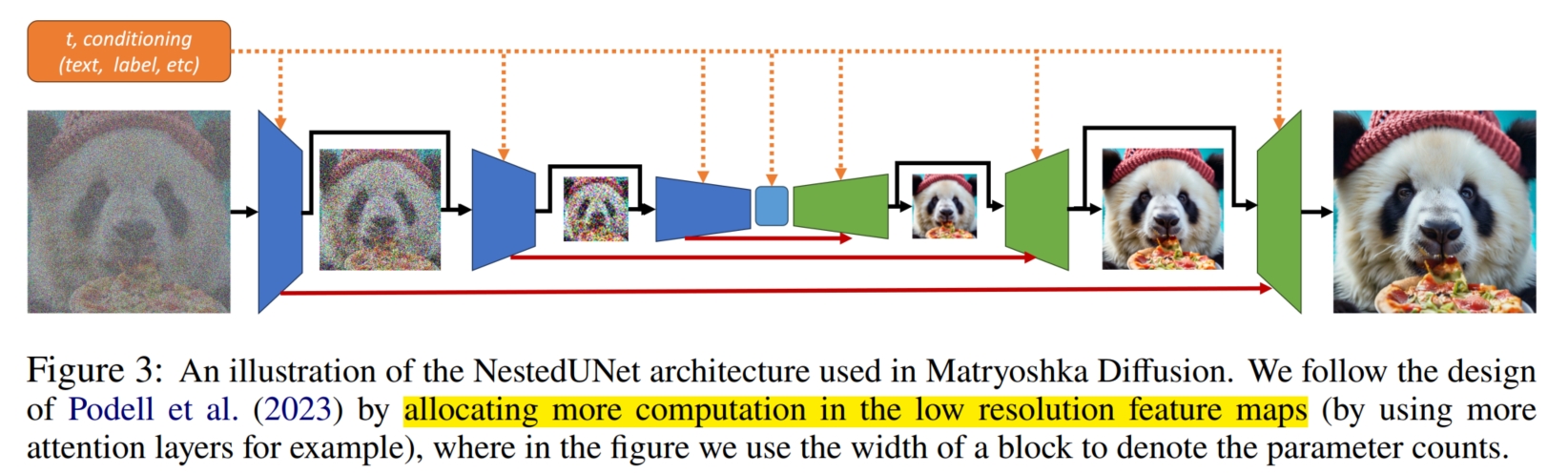
目前 DM 模型想要生成高分辨率的图像主要有 $2$ 种方式：一是先使用 DM 模型生成分辨率较低的图像，再通过超分 (super-resolution) 模型将分辨率较低的图像转化为高分辨率图像。 这就使得至少需要 2 个模型实现高分辨率；同时，由于是分开训练 DM 和超分模型，这就使得模型计算量的增加，同时生成质量受到 exposure bias 的限制。 第二种方法是将图像转化到维度(即分辨率)更低的潜变量空间，然后实现扩散生成，如 Stable-Diffusion (LDM)。 这种方法不仅增加了模型学习的复杂性(因为不仅要学习图像的潜变量，还要学习潜变量到像素图像之间的转化)，而且不可避免存在压缩损失 (lossy compression)。 通过上述分析，本文提出了 MDM 模型，结合了第一种方法直接在 pixel 空间上训练的好处，同时又结合了第二种方法 end-to-end 的生成过程(其实第二种方法也不能算 end-to-end，它还是需要从潜变量到 pixel 的后处理过程)。 MDM 模型通过融合了多分辨率图像生成的并行训练方式解决了 end-to-end 模型生成高分辨率图像的问题。其模型思想较为直观： 先前的模型通过 DM 直接生成高分辨率图像的效果不行，很可能主要是因为没有辅助的条件帮助模型学习，导致模型从零生成难度较大。如果能像第一种方法一样，给出低分辨率图像作为参考，模型生成的效率和质量应该会更高。 于是，问题便转化为如何将低分辨率图像的生成融合到高分辨率图像的生成中(即使用一个模型生成)，并使得高分辨率图像的生成能借助低分辨率的图像。 通过观察 U-net 架构(DM 模型最常用的架构)可以看到，U-net 模型主要包括 dowm-sample $F_d(·)$ (将图像 $I$ 下采样为潜表示 $I_l$), middle-fuse $F_m(·)$ (对 $I_l$ 进行进一步学习生成 $I_l'$) 和 up-sample $F_u(·)$ (对 $I_l'$ 进行上采样生成原始分辨率图像 $\hat{I}$)， 而我们知道， dowm-sample, middle-fuse 和 up-sample 都是对图像大小 unaware 的 (例如，对于一个下采样 $x$ 个像素的 down-sample 模块来说，无论输入多大 $h \times w$ 的图像，都是将其变成 $(h-x) \times (w-x)$)。 所以，一个 U-net 模型可以生成/处理任意分辨率的图像，就解决了使用一个模型生成任意分辨率图像的问题(其实简单归结就是使用 U-net 模型)。 而对于使用低分辨率图像辅助生成高分辨率图像，MDM 对 U-net 进行了改进，提出了 NestedUnet 模型(主要是在输入和输出连接上进行改变，如下伪代码)， 它首先生成低分辨率图像 $I^{low}$，再将已经生成好的低分辨率图像 $I^{low}$ 和 原始的高分辨率图像 $I^{high}$ 经过 down-sample 生成的潜表示 $I_l^{high} = F_d(I^{high})$ 相结合 $I^{low} + I_l^{high}$， 作为融合了低分辨率图像和原始高分辨率图像的更新潜表示 $I_{l-new}^{high}$，然后再使用 middle-fuse 进行进一步学习，生成 $I_{l-new}^{high}$$'$， 最后通过 up-sample 生成更新后的高分辨率图像 $\hat{I}^{high} = F_u(I_{l-new}^{high}$$')$， 这样便实现了使用低分辨率图像辅助高分辨率图像生成的目的。 同样地，也可以通过对高分辨率图像 $I^{high}$ 进行 2 次 down-sample 生成潜变量 $I_{ll}^{high} = F_d(F_d(I^{high}))$， 对低分辨率图像进行 1 次 down-sample 生成潜变量 $I_{l}^{low} = F_d(I^{low})$， 再将两者结合作为融合了原始低分辨率图像和高分辨率图像的更新潜表示 $I_{l-new}^{low} = I_{l}^{low} + I_{ll}^{high}$， 然后再使用 middle-fuse 进行进一步学习，生成 $I_{l-new}^{low}$$'$， 最后通过 up-sample 生成更新后的低分辨率图像 $\hat{I}^{low} = F_u(I_{l-new}^{low}$$')$， 这样便实现了使用高分辨率图像辅助低分辨率图像生成。NestedUnet 同时使用了这两种方式来促进高/低分辨率图像生成的学习(如下图)。

(ps: 这段代码非常有意思，建议使用 $z = [z_1,z_2,z_3]$ 进行手推一下递归过程，你就会被它惊艳到，如此复杂的融合过程可以写成如此简短优美的递归过程)

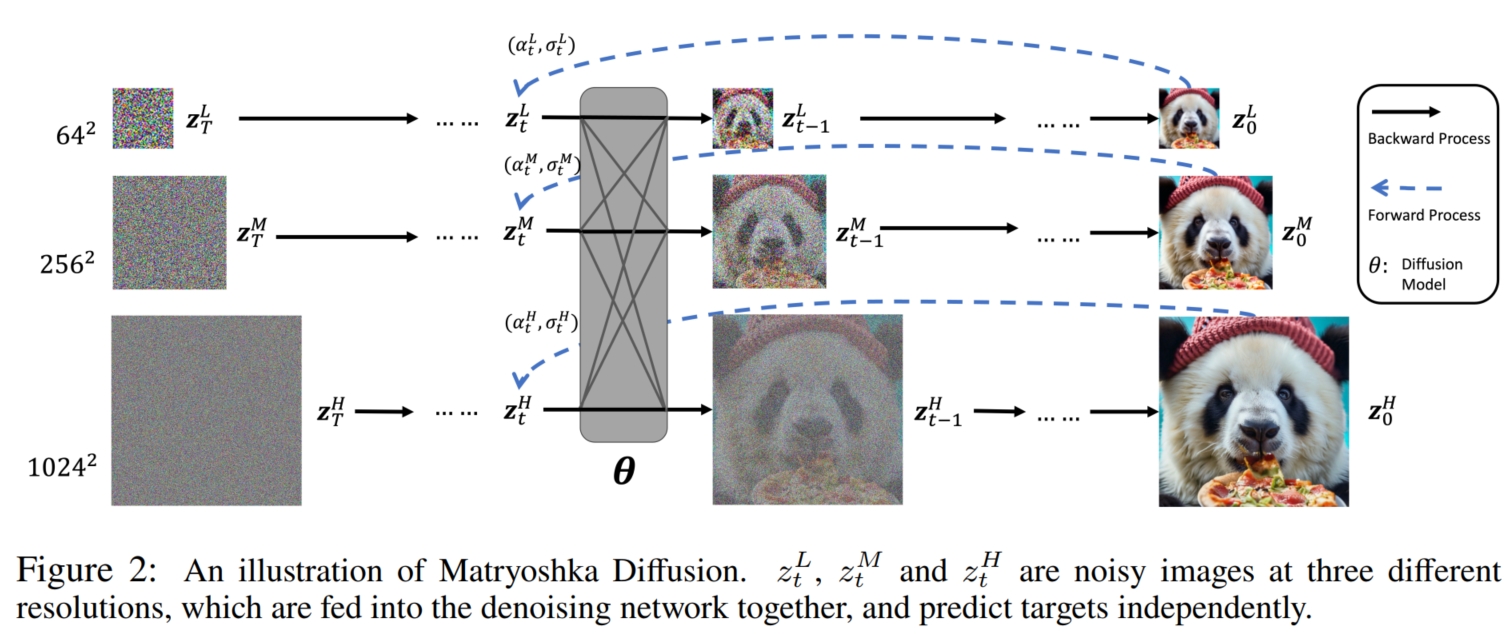
从数学证明上而言，MDM 生成了多个分辨率的图像以帮助最终的高分辨率图像的生成。对于给定的高分辨率图像 $x \in R^N$， 假设一共有 $R$ 个分辨率，其分辨率分别为 $R^{N_1},...,R^{N_R}, N_1 < ... N_R = N$ (这里使用一维向量代表图像，即 $h_i \times w_i = N_i$)。 对每个分辨率的图像分别加上第 $t$ 步的噪声即可生成第 $t$ 步的带噪图像 $z_t = [z_t^1,...,z_t^R] \in R^{N_1 + ... + N_R}$。 在 MDM 模型扩散的第 $t$ 步，其输入就是模型在第 $t+1$ 步生成的所有分辨率的图像(训练时是原始图像 $x$ 第 $t$ 步的带噪图像) $z_t = [z_t^1,...,z_t^R]$， 符合正态分布 $q(z_t^r|x) = N(z_t^r;\alpha_t^rD^r(x),{\sigma_t^r}^2I)$， 其中 $D^r(x): R^N \rightarrow R^{N_r}$ 表示 $x$ 在第 $r$ 个分辨率下的图像 $x_r \in R^{N_r}$，$D^r(·)$ 被称作 deterministic "down-sample" operator (如 $avgpool(·)$)； 而 $\{\alpha_t^r,\sigma_t^r\}$ 也是第 $r$ 个分辨率下的噪声参数。 然后 MDM 模型学习 $p_{\theta}(z_{t−1}|z_t)$ 与 $R$ 个 neural denoisers $x_{\theta}^{r}(z_t)$ 的反向过程 (根据上一段的分析，这 $R$ 个模型由一个 NestedUnet 模型替代)生成更新的所有分辨率的图像 $z_{t-1}$。 其中每个变量 $z_{t−1}^r$ 依赖于所有分辨率 $\{z_t^1...z_t^R\}$， 所以，其损失函数为 $l_{\theta} = E_{t \sim [1,T]}E_{z_t \sim q(z_t|x)} \sum_{r=1}^R{[\omega_t^r·||x_{\theta}^r(z_t,t) - D^r(x)||_2^2]}$。 而在 inference 过程中，MDM 模型并行生成所有 $R$ 个分辨率的图像(因为每个 $z_{t−1}^r$ 只依赖输入 $z_t$，而不依赖当前的输出 $z_{t-1}^1 \sim z_{t-1}^{r-1}$)。

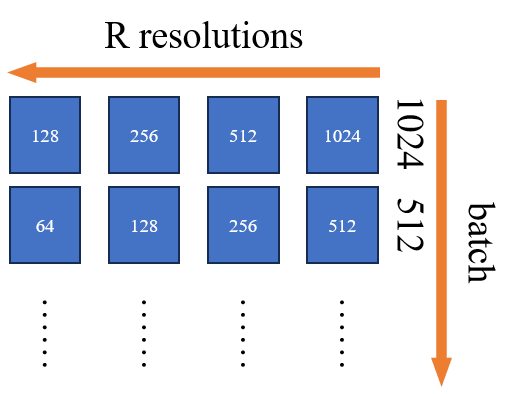
这种多分辨率图像生成的设计的好处是：(1) 由于在 inference 过程中关心的是全分辨率输出 $z_t^R$，所有其他中间分辨率都被视为额外的隐藏变量 $z_t^r$，用以丰富建模分布的复杂性; (2) 多分辨率依赖性实现了跨 $z_t^r$ 的共享权重和计算资源，使得模型能够以更有效的方式重新分配计算，以提高训练和推理效率(通常是将计算量倾斜于低分辨率图像的生成)。 为了进一步提高模型的收敛速度，本文将训练划分为 $R$ 阶段，在这些阶段中，逐步将更高的分辨率添加到 $L_{\theta}$ 的训练损失中。这相当于 MDM 模型从 $[z_t^1]$ 开始训练， 每个阶段增加一个分辨率，得到 $[z_t^1,...,z_t^r]$，直到使用所有分辨率的图像 $[z_t^1,...,z_t^R]$ 进行训练。 该训练方式从一开始就避免了昂贵的高分辨率训练(即一开始模型是啥也不会，基本上只专注于学低分辨率的图像生成，输入高分辨率图像基本上没什么用，还占用计算资源和空间)，并加快了整体收敛速度。 此外，还可以添加混合分辨率的训练方式，这是一种在单个 batch 中对具有不同最终分辨率的样本进行并发训练的技术 (即一个 batch 中既有 $1024 \times 1024$ 的图像，又有 $512 \times 512$ 的图像。 注意：这里的不同分辨率和 NestedUnet 中的不同分辨率不一样，属于横纵关系： 如，对于 batch 中 $1024 \times 1024$ 的图像，NestedUnet 在训练时额外生成 $512 \times 512$ 的低分辨率图像，而不是将 batch 中的 $512 \times 512$ 拿来使用，其训练数据表示如下图)。