论文题目：Multipattern Mining Using Pattern-Level Contrastive Learning and Multipattern Activation Map

发表期刊：IEEE Transactions on Neural Networks and Learning Systems(TNNLS 2022, 2023年 CCF B)

第一作者：Xuefeng Liang(Professor with Xidian University)；h指数 18(2023)

Question

文章主要解决的问题是如何在不知道 visual pattern 的 label 和 number 的情况下找出某一类图像的所有 visual patterns。

Preliminary

visual pattern：它是一种临界于 pixel 和 category label 之间的语义特征，即它的语义信息比单纯的像素高，但是又低于图像本身的类别。一类图像中可以包含多个 visual patterns，它们都独特地描述了该类图像(即其他图像不存在或者不是其他图像的显著性特征)。 一个通俗直观的例子是，对于西安的鼓楼，所有的 鼓楼 照片都有 category label —— 鼓楼；而鼓楼中含有其标志性代表 鼓 和 楼，它们两个就是 鼓楼 这类图像的 visual pattern。 虽然其不一定都在每张 鼓楼 照片中出现，但是每张照片都至少出现一个 visual patter，且统计下来，这两个 visual pattern 在 鼓楼 照片中出现的次数远超其他类别,同时它们又都带有一定的语义信息，所以它们便是 鼓楼 类照片的 visual patterns。 然而对于更加广泛的 visual pattern 来说，它们的语义信息可能不如前面那个例子那么直观，例如纹理等，一方面给每类图像标记 visual pattern 标签是一类难题；另一方面人工寻找每类图像的每个 visual pattern 也是一类难题。 因此，现在的方法大部分都使用模型输出的 feature 作为每类图像的 visual pattern(例如 CNN 卷积层输出的 activation)。 虽然其相较 鼓、楼 这种实质性标签难以理解，但是好处是不需要确定其具体含义(这样就不需要费力进行 visual pattern 标签标记)，同时其也含有和实质性标签本质一样的语义信息。

Contrastive Learning：对比学习是最近十分火热的无监督学习方法，它通过构造 self-supervision 来实现网络训练。 大体上，对比学习采用两个网络(分别叫 online network 和 target network)进行训练，online network 输入原始图像，其输出一段 vector 作为特征 $f_1$， 而 target network 输入对应原始图像的正样本(它与原始图像互为正样本对，通常是原始图像通过数据增强得来，比如旋转)，其也输出一段 vector 作为 $f_1$ 的正样本特征 $f_2$。 对于 $f_1$ 和 $f_2$，我们希望它们两的特征应该相似，所以可以使得它们的相似度函数 $sim(f_1, f_2)$(最简单的是点乘，然后正则化：$\frac{f_1f_2^T}{\sqrt{f_1f_1^T}\sqrt{f_2f_2^T}}$)的值接近 1。 然而这种方法有一定的弊端， 那就是模型可能会找到一条”捷径“，online network 和 target network 对于每一个输入，都输出相同的 vector(比如全 0)，这样就可以保证每个正样本对之间的相似度为 1。 因此，我们需要引入负样本(通常是和原始图像不同的任意其他图像，其通过 target network 的输出向量为 $f_3$)来限制模型的输出。 我们希望 $f_1$ 和 $f_3$ 应该不相似，所以可以使得它们的相似度函数 $sim(f_1, f_3)$ 的值接近 0。 通常而言每个原始图像的正样本就一个，而负样本可以很多个(一个直观的理解是对于负样本，模型可以很容易判断其和原始图像不相似，如果就只使用一个负样本，则会导致负样本基本上没贡献)。 这就和传统的分类问题较为相似(把正确的类别看作正样本，其他类别均看作负样本)， 因此可以使用 BCE loss 进行训练：$-log\frac{exp(sim(f_i,f_+)/\tau)}{\sum_{j,f_j \neq f_+}^{N}{exp(sim(f_i, f_j)\tau)}+exp(sim(f_i,f_+)/\tau}$。 其中 $\tau$ 表示温度因子，其越小则使得不相似的负样本的影响越大(可以简单理解：exp函数在 $[0,1/\tau)$ 的区间内的趋势随着 $\tau$ 的增大越趋于平稳， 由于 $sim(·,·)$ 函数最大值为 1，若 $\tau$ 越大，则会使得 $sim(·,·)/\tau$ 的值域越趋于 0，则经过 $exp$ 函数后使得 $sim(·,·) = 1$ 和 $sim(·,·) = 0$ 的值越相似， 就使得各个样本之间的相似度差值对模型的训练影响越小(无论是与原始样本 $f_o$ 相似度很大的负样本($sim(·,·) \approx 1$)，还是相似度很小的负样本($sim(·,·) \approx 0$)，其对模型训练的贡献都差不多)。 最终训练出来的 online network 具有很好的模型先验，可以送到下游任务进行微调使用。

Method

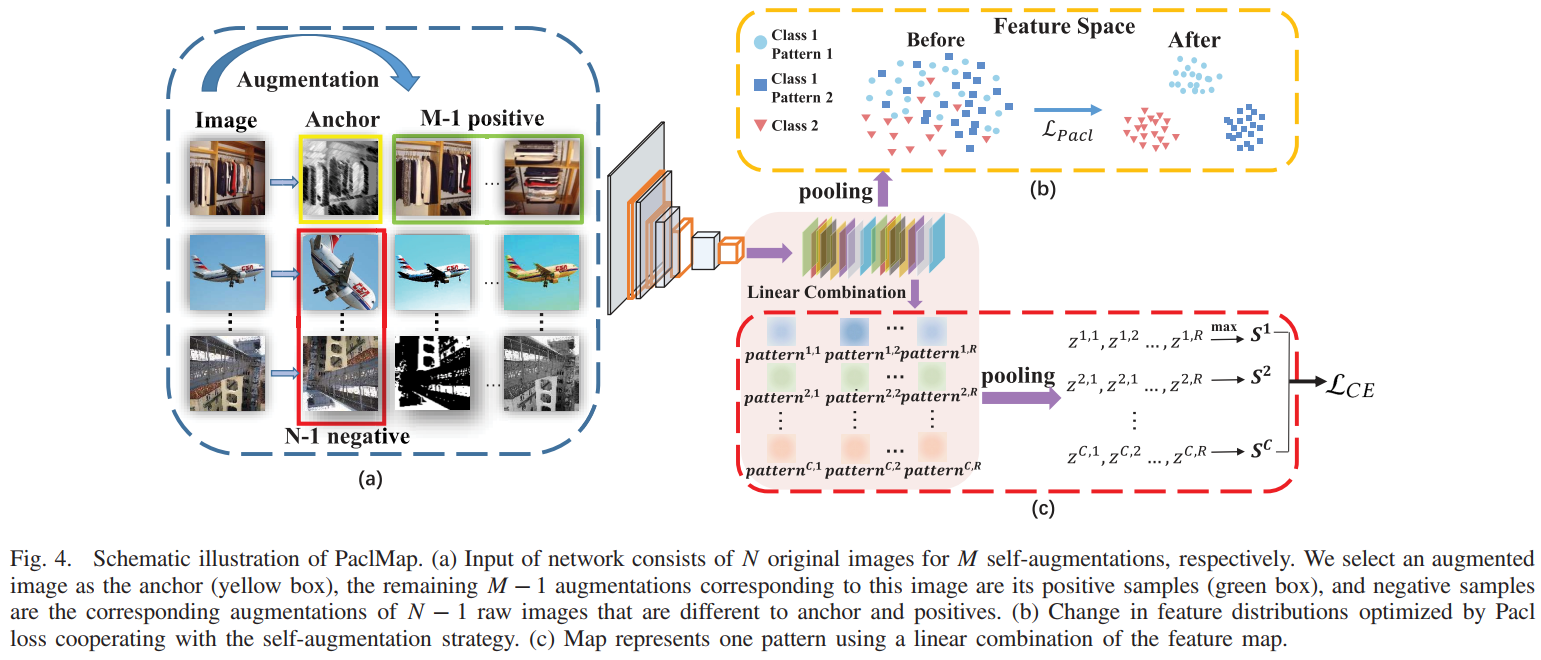
在之前的方法中，它们都假设每类图像只存在一个 visual pattern， 这样就可以通过构造 category label 到 visual pattern 之间的一一映射以获得 visual pattern。 但是本文认为每类图像不止一个 visual pattern，需要在仅仅知道 category label 的情况下将它们都找出来。 一般来说，visual pattern包含两个特点：discrimination 和 frequency。 discrimination 表示其具有可判别性，而不是笼统的语义信息(例如 山 这个语义信息就具有笼统性)；frequency 表示其应该在该类图像中频繁出现。

因此，针对 frequency，本文提出了 Pacl 模块。其对于对比学习的整体框架没有改变，只是改变了损失函数和正负样本的选择。 其中，对于负样本，由于我们需要减少错误的负样本对于模型学习的影响，而错误的负样本提出与原始样本（anchor)相似度较高，所以本文选择较大的 $\tau$。 同时，对于相似度函数，本文采用 $cos^2(·|·)$，因为我们希望原始样本和负样本以及各个负样本之间不存在相关性。 如果使用 $cos(·|·)$，则 $= 0$ 时，各个负样本的向量都与原始样本垂直，则各个负样本相互平行(即相关)； 而使用 $cos^2(·|·)$，当各个负样本的向量都与原始样本垂直时，各个负样本不相互平行(即不相关)。 对于正样本，由于对比学习的正样本仅有一对，导致其学习到的特征更多的是当前图像的特征(它可能包含了不必要的细节，即 more fine-grained)。 因此 Pacl 通过构造多组 postive-anchor 对来鼓励模型学习更为一致性的特征。 具体而言(如图1中 (a))，每个 batch 包含 $N$ 个原始图像的 $M$ 个数据增强。首先选择一个增强后的图像作为 anchor(黄色框)， 然后使用其他 $M - 1$ 增强后的图像作为正样本(绿色框)，并使 $M - 1 > (N - 1)/C$ (其中 $C$ 是数据集中类别的数量)。 负样本(红框)包含其他 $N - 1$ 个原始图像的增强。并且 batch 中的所有 $N × M$ 张图像依次被选为 anchor 进行训练。 得到损失函数为 $L_{Pacl} = -\frac{1}{M-1}log\frac{\sum_{i=1}^{M-1}exp(sim(f_o,f_{i+})/\tau)}{\sum_{i=1}^{M-1}{exp(sim(f_o,f_{i+})/\tau)} + \sum_{j=1}^{N-1}{exp(sim(f_o,f_{j-})/\tau)}}。$ Pacl之所以可以学习到 frequency，我的理解是对比学习本身的优势。 举个简单的例子，经过对比学习之后，可能模型对 松 这个概念有了一个统一的理解(虽然模型并不知道它叫松)，对于每张出现 松 的图像它都可以辨别出来， 但是这时它学到的 pattern 太笼统了(它仅仅只是对松有理解，而我们更希望它学习到 黄山迎客松 这种更具有 discriminative 的 pattern)，就需要进一步对其 discriminarion 进行学习。

因此，针对 discrimination，本文提出了 Map 模块。由于本文的是 multipattern，即多对一的映射，因此不能直接转化为一对一的分类问题。 在 visual pattern 中讲过，目前的方法大都使用模型输出的 feature 作为 pattern，但是并不是简单地把 feature 直接等于 pattern，一般是将最后一层 conv 输出的 feature maps 进行线性结合形成一个 pattern。 由于本文讨论的是 multipattern，所以需要输出多个 pattern，它采用的方法和卷积有些相似，即通过不同的线性权重 $\omega_i^j$ 来获得不同的 pattern $P^j$。 具体而言，对于最后一层卷积输出的 feature maps $V = \{V_1,...,V_K\}$，定义一个最大可能的 pattern 数量为 $R$，使用 $R$ 组权重(每组 $K$ 个)来获得每类图像的 $R$ 个 pattern(称为 Map，每个 pattern 称为 PAM)：$PAM^{c,r} = \sum_k{\omega_k^{c,r}V_k}$。 这样一来，$K$ 个 feature maps 就生成了 $C * R$ 个 PAM。接下来便是如何将它们与一一映射的分类问题结合起来，以实现训练。 因为 category label本身具有非常强的 discrimination 特性，以它为监督信号优化得到的 pattern 会比单纯对比学习的 pattern 的 discrimination 更强。 因此，本文首先对每个 PAM 进行降维，即使用 global average pooling 将每个 PAM 降为 1 个实数($H * W \rightarrow 1$)：$z^{c,r} = avgpool\{PAM^{c,r}|r=1,...,R\}$。 接着再使用 max 函数将每类的 $R$ 个 PAM 减少至 1 个：$S^c = max\{z^{c,r}|r=1,...,R\}$，这样就可以把 $C$ 个 $S^c$ 和 $C$ 个类别对应起来。 再经过 softmax 正则化后；$\widehat{y^c} = \frac{exp(S^c)}{\sum_c{exp(S^c)}}$。 最后就可以使用 cross entropy 损失进行训练：$L_{CE} = \frac{1}{N}\sum_{n=1}^N{(\sum_{c=1}^C{(-y^clog\widehat{y^c})})}$。

因此，最后的损失函数为 $L = \lambda * L_{CE} + (1-\lambda) * L_{Pacl}。$