论文题目：Retentive Network: A Successor to Transformer for Large Language Models

发表会议：截至2023年10月19日暂无，论文版本为 arxiv-v4

第一作者：Yutao Sun(Tsinghua University)

参考资料：一文理解RetNet

Question

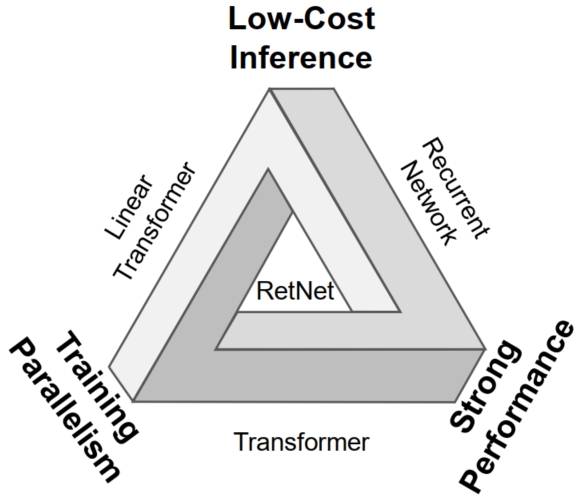
如何设计出一种模型架构，能够打破不可能三角的限制，即既要保持 training parallelism, 又要实现 low-cost inference, 同时还要有 strong performance.

Method(Mathematical)

首先可以明确一点，寻找单一的架构打破不可能三角几乎是无法做到的，所以可行的方法便是通过结合不同架构之间的优势来实现。 而本文通过分析，可以发现传统的 RNN 模型在 inference 时的时间复杂度为 $O(1)$，但是它无法实现并行训练； 而 transformer 可以实现并行训练，但是其 inference 的时间复杂度为 $O(N)$，同时它们都具有 strong performance。 如果能将 RNN 模型和 transformer 模型结合，就可以实现打破不可能三角，但是问题在于如何能将两者结合，使得它们既使用同一套参数，又能实现不同的架构效果。 于是本文便提出了 RetNet，可以在使用相同参数的情况下同时支持三个计算范式：1) parallel; 2) recurrent; 3) chunk-wise recurrent。

RetNet 架构和 Transformer 相似，都是由一个个 RetNet block 组成，每个 block 包含一个 multi-scale retention (MSR) 和一个 feed-forward network (FFN). 而 FFN 与 Transformer 一致，因此下面就详细讲解 MSR. 由于 RetNet 的 parallel (对应 transformer) 和 recurrent (对应 RNN) 使用的是同一套参数，我们就需要数学推导来证明 RNN 可以通过一定的转化变成 transformer. 具体而言，首先给定一个输入序列 $\{x_i\}_{i=1}^{|x|}$，其中 $|x|$ 表示序列的长度。然后经过 word embedding 层得到词嵌入向量：

• 然后对 $X$ 的每个词 $X_n \in R^{1 \times d}$ 乘上权重 $\omega_V \in R^{d \times d}$ 得到 $v_n \in R^{1 \times d}$：$V_n = X_n · \omega_V$。 同时和 transformer 相似，通过 $W_Q \in R^{d \times d}$ 和 $W_K \in R^{d \times d}$ 计算 $Q$ 和 $K$：$Q = XW_Q,\ K = XW_K$

  由于我们是要从 RNN 推算到 transformer，因此我们先要从 RNN 开始。 它包含了一个隐藏状态 $s_n \in R^{d \times d}$ 和 一个输出 $o_n \in R^{1 \times d}$ 的计算：

  $s_n = AS_{n-1} + K_n^Tv_n$ $o_n = Q_ns_n = \sum_{m=1}^n{Q_nA^{n-m}K_m^Tv_m}$

  其中 $A \in R^{d \times d}$ 是一个矩阵，$K_n \in R^{1 \times d}$ 表示 K 中的第 n 个词所对应的 key。 同样 $Q_n \in R^{1 \times d}$ 表示 Q 中的第 n 个词对应的 query。 对于 $o_n$ 从 $Q_ns_n$ 到 $\sum_{m=1}^n{Q_nA^{n-m}K_m^Tv_m}$ 的推理，只需要假设 $s_0$ 为全 0 矩阵进行归纳推理即可得到。

• 本文定义 A 矩阵为 diagonalizable(可对角化) 矩阵，则可以将 A 分解为：

  $A = \Lambda \lambda \Lambda^{-1} = \Lambda (\gamma e^{i\theta}) \Lambda^{-1}$

  其中 $\gamma$ 和 $\theta \in R^{1 \times d} | R^{d \times 1}$，$\lambda$ 是一个对角矩阵，$\Lambda$ 是一个可逆矩阵。 下面推导如何从 $\lambda$ 转化为 $\gamma e^{i\theta}$：首先需要理解 $e^{ix}$ 是一个欧拉公式，将其转化为复数可得 $e^{ix} = cos\ x + isin\ x$。 而 $\theta$ 是一个 $d$ 维向量，所以根据欧拉公式可得 $e^{i\theta} = [cos\theta_1+sin\theta_1...,cos\theta_d+sin\theta_d] \in R^{d \times d}$。 因为 $\gamma$ 也是一个 $d$ 维向量，所以两者相乘($d \times 1 · 1 \times d = d \times d$)便可得到 $d \times d$的矩阵 $\lambda$。 对角元素的值就对应将 $\gamma$ 和 $e^{i\theta}$ 转成复数向量相乘再将结果转回实数向量的结果。

  通过将矩阵 $A$ 对角化，则可以将 $o_n$ 的计算公式中的 $A^{n-m}$ 展开为 $A^{n-m} = \Lambda (\gamma e^{i\theta})^{n-m} \Lambda^{-1}\ (\Lambda^{-1}\Lambda = 1)$。 将展开式带入到 $o_n$ 的计算公式中可得：

  $o_n = \sum_{m=1}^n{Q_nA^{n-m}K_m^Tv_m} \\ = \sum_{m=1}^n{Q_n(\Lambda (\gamma e^{i\theta})^{n-m} \Lambda^{-1})K_m^Tv_m} \\ = \sum_{m=1}^n{X_nW_Q(\Lambda (\gamma e^{i\theta})^{n-m} \Lambda^{-1})(X_mW_K)^Tv_m} \\ = \sum_{m=1}^n{X_nW_Q\Lambda (\gamma e^{i\theta})^{n-m} \Lambda^{-1}W_K^TX_m^Tv_m}$

• 由于 $W_Q, W_K, \Lambda$ 都是可学习参数，所以可以将 $\Lambda$ 融合进 $W_Q, W_K$ 中当作一个参数学习， 即 $W_Q = W_Q\Lambda, W_K^T = \Lambda^{-1} W_K^T$。则可以进一步简化 $o_n$ 的计算公式：

  $o_n = \sum_{m=1}^n{Q_n(\gamma e^{i\theta})^{n-m}K_m^Tv_m} \\ = \sum_{m=1}^n{Q_n(\gamma e^{i\theta})^{n}(\gamma e^{i\theta})^{-m}K_m^Tv_m} \\ = \sum_{m=1}^n{Q_n(\gamma e^{i\theta})^{n}(K_m(\gamma e^{i\theta})^{-m})^Tv_m} \\ = \sum_{m=1}^n{Q_n(\gamma^n e^{in\theta})(K_m(\gamma^{-m} e^{i(-m)\theta}))^Tv_m}$

• 接着将公式继续简化，将 $\gamma$ 设为一个 scaler $\in R$，这样就可以将它提到外面：$o_n = \sum_{m=1}^n{\gamma^{n-m}(Q_ne^{in\theta})((K_me^{i(-m)\theta}))^Tv_m}$ (之前不能提出来是因为在前面的推导中我们将其视为一个 $d$ 维的向量，而向量的乘法不具有交换律)。

• 然后根据欧拉公式：

  $e^{i(-m)\theta} = [cos(-m\theta_1)+sin(-m\theta_1),...,cos(-m\theta_d)+sin(-m\theta_d)] \\ = [cos\ m\theta_1-sin\ m\theta_1,...,cos\ m\theta_d-sin\ m\theta_d] = e^{im\theta T*}$

  其中 $T*$ 表示复数共轭转置，所以 $o_n$ 的计算公式可以进一步简化为 $o_n = \sum_{m=1}^n{\gamma^{n-m}(Q_ne^{in\theta})((K_me^{i(m)\theta}))^{T*}v_m}$ (对于实数向量 $K_m$，其复数共轭转置对于自身的转置，所以不影响)。

由于 $Q_n, K_m, v_m, e^{in\theta}/e^{im\theta}, \gamma^{n-m}$ 都可以并行计算得出，所以 $\sum_{m=1}^n$ 的操作只需一步便可计算出 $o_n$。 而不像最开始的需要计算出每个 $s_n$ 后再计算 $o_n$ 的 $n$ 步 操作。这样便完成了由 RNN 到 transformer ($n$ 步操作到 $1$ 步操作)的转化证明，而且参数基本相同。

Method(apply)

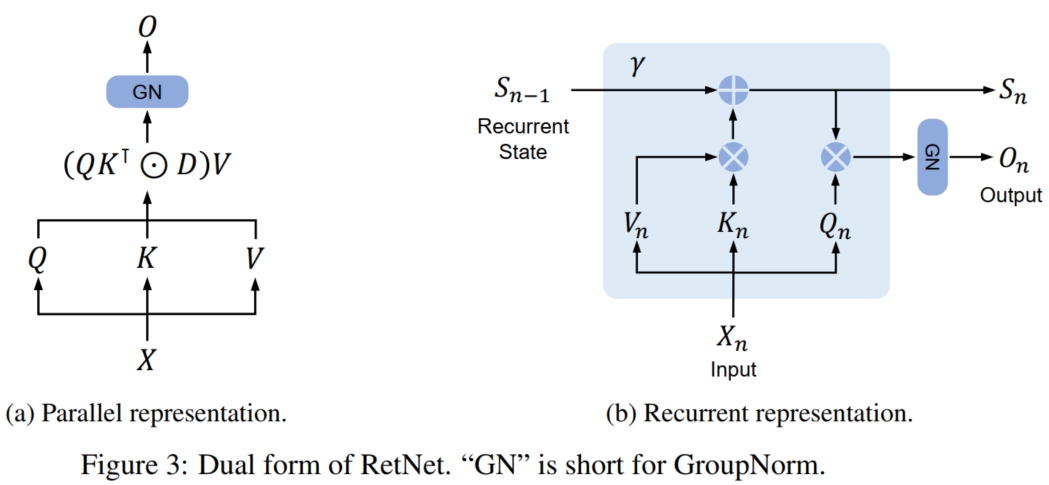
所以根据上面的推导，可以在训练的时候选择 transformer 的 $1$ 步操作模式提高训练并行性，而在预测时选择 RNN 的 $n$ 步操作模式提高推理速度。 具体而言，RetNet 将这两种模式分别命名为 Parallel 和 Recurrent。

• Parallel：在这种模式下，RetNet 类似于 transformer，通过计算 $K,Q,V$ 并进行注意力机制来提高并行性。 具体而言，本文计算 $Q,K,V$ 和输出 $O$ 的公式为(其中 $\bar{\Theta}$ 是 $\Theta$ 的复数共轭)：

  $Q = (XW_Q) \bigodot \Theta, K = (XW_K) \bigodot \bar{\Theta}, V = XW_V$ $\Theta_n = e^{in\theta}, D_{nm} = \begin{cases} \gamma^{n-m}, n \geq m \\ 0, n < m \end{cases} \in R^{|x| \times |x|}$ $O = Retention(X) = (QK^T \bigodot D)V$

• Recurrent：在这种模式下，RetNet 类似于 RNN， 通过 $O(1)$ 的计算复杂度计算隐藏状态 $S_n$ 和 输出 $O_n$ 进行序列计算来提高推理速度。 具体而言，本文计算 $S_n, O_n$ 的公式为(其中的 $Q,K,V,\gamma$ 和 Parallel 模式的是一样的参数)：

  $S_n = \gamma S_{n-1} + K_n^TV_n$ $O_n= Retention(X_n) = Q_nS_n,\ n = 1,...,|x|$

  可以看到 Recurrent 模式下就是把 Parallel 模式下的计算顺序修改， 改为先计算 $K_n$ 和 $V_n$ 的相乘然后一直累加到状态矩阵 $S_n$ 上，最后再和 $Q_n$ 相乘。 而不是像 Parallel 模式那样，每个词的计算要先算 $Q_n$ 和前面所有词的 $K$ 相乘得到 attention 权值再和 $V$ 相乘求和，这样就需要一直保留历史的 $K$ 和 $V$， 导致模型的内存消耗很大。

• Chunk-wise Recurrent：通过将 Parallel 模式和 Recurrent 模型相结合， 可以得到训练速度和推理速度居中的模式。具体的结合方式为：本文将输入序列划分为块。在每个块内，按照 Parallel 模型进行计算。相比之下，跨块信息按照 Recurrent 模式传递：

  $Q_{[i]} = Q_{Bi:B(i+1)}, K_{[i]} = K_{Bi:B(i+1)}, V_{[i]} = V_{Bi:B(i+1)}$ $R_i = K_{[i]}^T(V_{[i]} \bigodot \zeta + \gamma^BR_{i-1}, \zeta_{ij} = \gamma^{B-i-1})$ $Retention(X_{[i]} = (Q_{[i]}K_{[i]}^T \bigodot D)V_{[i]} + (Q{[i]}R_{i-1}) \bigodot \xi, \xi_{ij} = \gamma^{i+1}$

  其中 $(Q_{[i]}K_{[i]}^T \bigodot D)V_{[i]}$ 表示 Inner-Chunk，即 Parallel 模式； $(Q{[i]}R_{i-1}) \bigodot \xi$ 表示 Cross-Chunk，即 Recurrent 模式。

在训练过程中，本文使用 Parallel 模式和 Chunk-wise Recurrent 模式。 序列或块内的并行化可以有效地利用 gpu 来加速计算。更有利的是，Chunk-wise Recurrent 对于长序列训练特别有用，它在计算量和内存消耗方面都很高效。 而在推理过程中使用了 Recurrent 模式，很好地拟合了自回归解码。O(1)的复杂度降低了内存和推理延迟，同时达到了和 transformer 相同的结果。

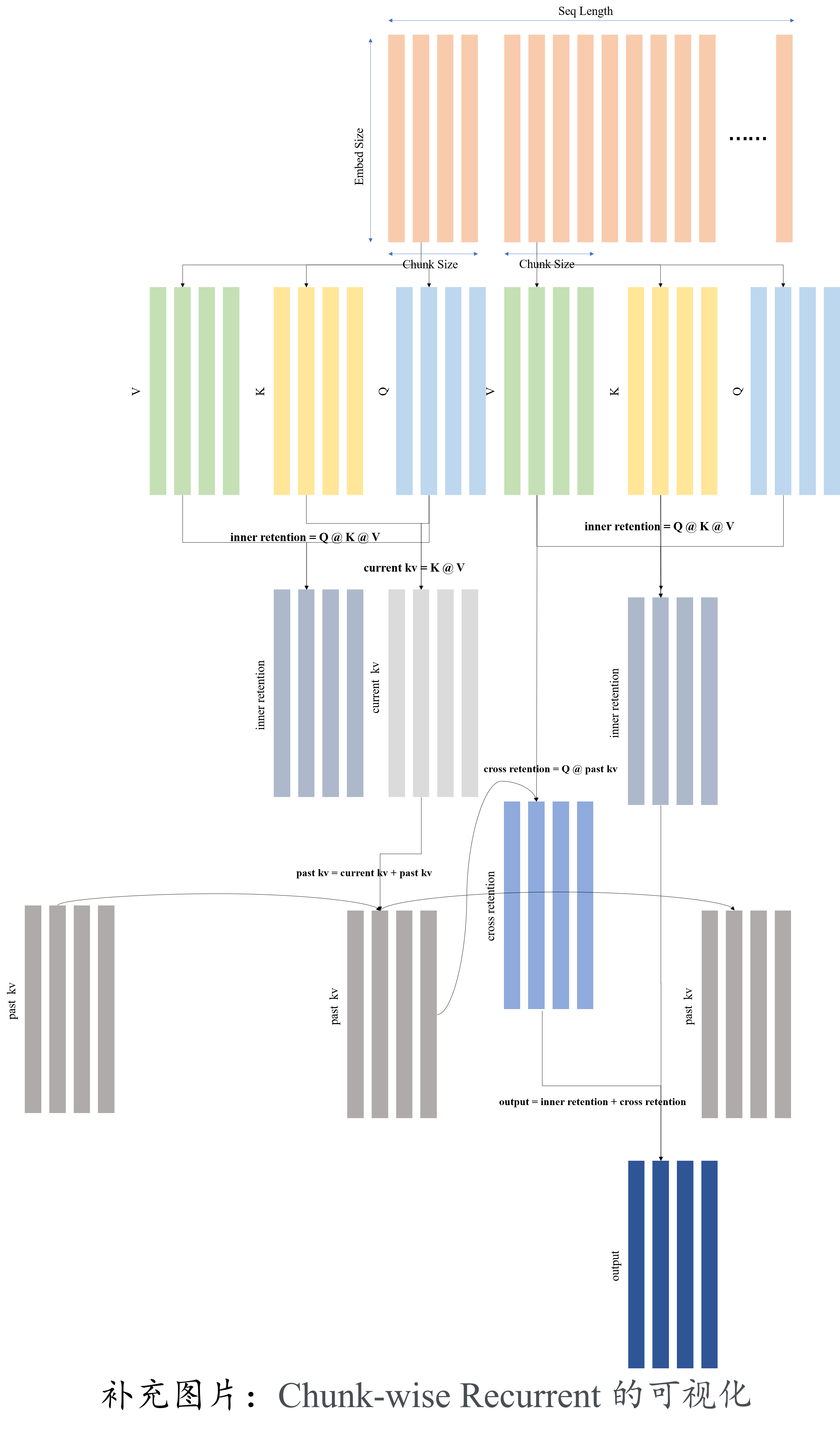
后续补充：1. 对角性质的证明；2. 如何将 Parallent 模式的公式变换回 Recurrent 模式。