论文题目：Sheared LLaMA: Accelerating Language Model Pre-training via Structured Pruning

发表会议：截至2023年10月21日暂无，论文版本为 arxiv-v1

第一作者：Mengzhou Xia(Princeton University)

Question

如何通过利用现有的 pre-trained LLM(大模型，如 LLaMA2-7B)，得到一个较小的(如 1.3B)且性能和同等规模的模型(如 LLaMA2-1.3B)相似的 LLM, 并且使用的计算量比从头训练一个同等规模的 LLM 少得多

Method

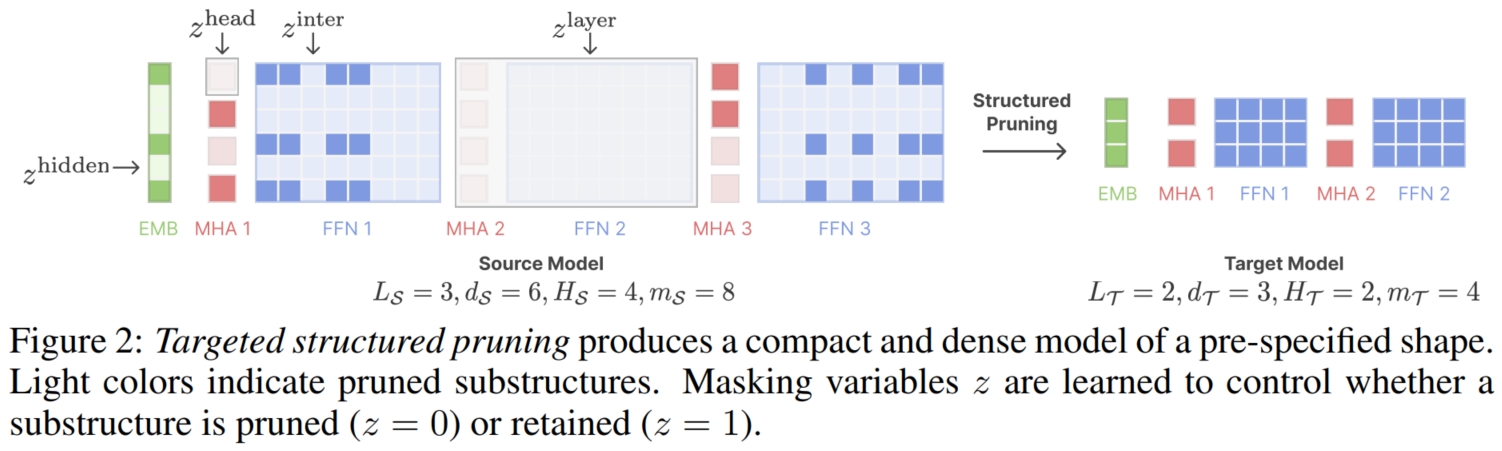
首先要从一个以及训练好的大模型获得高性能的小模型最直观也是最主流的方法就是模型剪枝(pruning；当然 student-teacher 架构也是一种解决方法，但是需要训练 student 模型 from scratch)。 但是 pruning 有 2 个问题需要解决：

1) 如何设计小模型的架构，使其拥有良好的性能和高效推理的潜力？ 2) 如何继续训练剪枝好的小模型使其达到理想性能？

本文就针对这 2 个问题分别给出了自己的解决思路。 首先是模型的架构，本文观察到现有的 structed pruning 方法往往会导致模型架构偏离流行的架构，并且作者假设现有的模型架构一般都是经过重重验证的，在各方面的性能潜力应该都是不错的。 与其使用无约束的 structed pruning 并承担导致模型架构畸形的风险，不如添加约束使得 structed pruning 将模型剪枝到指定的模型架构上。 具体而言，本文提出了 target structed pruning，通过在不同粒度上学习大模型参数上的一组剪枝掩码(pruning mask)， 从 global，如 layers 和 hidden dimentions，到 local，如 attention heads 和 intermediate dimensions。 以普通的 Transformer为例，其中，layers 就是对每一个 transformer block 都学习一个掩码数值 $0$ 或 $1$ 来选择是否保留该 block； hidden dimentions 就是 Embedding 层将原始数据转换成的潜表示所包含的维度数量(即通道数)，通过给每个维度学习一个掩码数值来选择是否保留该维度， 之所以它们俩是 global 的，是因为它们是在整个模型角度来进行考虑的。 而 attention heads 就是对每个 Transformer block 中的每一个 attention head 都学习一个掩码数值来选择是否保留； 而 intermediate dimensions 就是每个 Transformer block 中的 FFN 的中间表示的维度数量，通过给每个 Transformer block 中的 FFN 的中间表示的每个维度学习一个掩码数值来选择是否保留该维度， 之所以它们俩是 local 的，是因为它们是在每个 Transformer block 角度来进行考虑的。 假设源模型，即大模型 $M_S$ 的 hidden dimention 为 $d_S$, 有 $L_S$ 层，每一层包括 $1$ 个 Multi-head Attention (MHA) 和一个 FFN， 每个 MHA 中 head 的数量为 $H_S$，每个 FFN 的 intermediate dimensions 为 $m_S$，则可以设计如下掩码：

例如，其中的 $z^{layer}$ 表示 $L_S$ 层 Transforner Block 的掩码，$z_i^{layer} = 0$ 表示 $i$ 层的 Transforner Block 舍弃；反之则表示保留。 接着便是如何将掩码融入到剪枝优化过程中以限制模型的架构。很明显这是一个约束的优化问题，最常用的方法便是 Lagrange multipliers 法。 例如，假设目标模型，即小模型的每个 MHA 的 head 数量为 $H_T$，则关于以 $H_T$ 为约束条件的损失函数为： $\widetilde{L}^{head}(\lambda, \theta, z) = \lambda^{head} · (\sum{z^{head}} - H_T) + \phi^{head} · (\sum{z^{head}} - H_T)^2$。 最终，通过联合优化模型参数(model weights；以模型性能为损失函数)和剪枝掩码(pruning masks)便可进行剪枝训练：

其中 $L(\theta, z)$ 表示 language modeling loss，使用的模型权重是经 pruning mask 掩码后的 (注意，这里的模型权重还都是从大模型直接复制而来的，在 target structed pruning 训练时更新的参数只是 pruning mask)。 由于每个 mask $z$ 都是 $[0,1]$ 之间的实数向量(和分数相似)，所以最终的选择策略是选择前 $H_T/L_T/d_T/m_T$ 高的分数对应位置的模型参数保留，其余丢弃。

接着便是继续训练剪枝好的小模型，这里可能有一个疑问，为什么不直接在 target structed pruning 阶段让模型参数也一起训练更新？ 首先，pruning 是一个相对较慢的过程(比标准的 LLM 训练慢 5 倍)，而本文发现 pruning mask 的学习过程通过是很快收敛的，即很快就学习到了最终的 pruning mask 模式。 其次，如果仅仅在 pruning mask 收敛期间对模型参数进行更新，可能会适得其反，恶化模型的性能，所以便把模型参数的再训练单独进行。 训练剪枝模型的最直观方法是将训练大模型的数据集直接给小模型继续训练，直到达到预期性能。 但是这样有一个问题：对于大模型来说，它的训练是从头开始的，即它的初始状态是对各个 domain 的学习程度 $=0$；而对于剪枝得到的小模型，它本身对不同的 domain 存在一定的、各不相同的学习程度 (本文通过分析和实验证明了剪枝小模型一般对 low-entropy 且小型的 domain (例如 Github) 保留有较多的知识，而对于 high-entropy 且大型的 domain (例如 C4) 保留的知识较少)， 如果再直接将大模型训练的数据集给小模型训练，则会导致数据利用的 inefficient (即对于 low-entropy 且小型的 domain 学习的很快，但是对于 high-entropy 且大型的 domain 学的很慢)， 进而有损模型性能，所以就需要对数据集进行采样以平衡小模型在训练时对各个 domain 的学习程度。 于是本文便提出了 dynamic batch loading 的数据集采样方式。 这里便引出了 2 个新的问题：1) 如何定义模型对每个 domain 的学习程度；2) 训练时该和谁去对齐每个 domain 的学习程度以调整数据集的采样。 对于第一个问题，本文采用模型在每个 domain 上的 loss 来近似定义模型对每个 domain 的学习程度：loss 越低则表示在该 domain 的学习程度较低；反之则表示在该 domain 的学习程度较高。 而对于第二个问题，这里本文还是假设大模型 pre-trained 的最终模型结果是较为优质的，则与大模型在每个 domain 上的最终 loss 进行对齐就可以调整数据集的采样。 具体而言，假设训练数据集有 $k$ 个 domains：$D_1,...,D_k$，每个 domain 还有一个验证集 $D_v^{val}$ 用于小模型的对齐。 首先将大模型在每个 domain 的 loss 设为参考 loss：$l_{ref}(D_i)$，需要在训练过程中不断对齐 $l_{ref}(D_i)$。 由于每个 loss 的量纲可能不同，所以比较绝对大小没有意义，而最常见的是将小模型当前的 loss 减去参考 loss，并用参考 loss 进行归一化后，就能说明每个 domain 的学习情况， 本文采用了更高级的方法来更新，即每过 $m$ 次训练迭代，模型便在 $D_i^{val}$ 中测试每个 domain 的 loss $l_t$ (假设当前是 step $t$)。 然后更新数据集的采样权重 $\omega_t$，模型学习程度较低的应该多采样，而学习程度较高的应该少采样，所以采样权重的更新公式为(exponential ascent)：

最后获得 $\omega_t$ 便是新一轮的数据集采样权重，循环 $m$ 往复，便可进行训练。dynamic batch loading 的整个算法流程如下图。 可以看到虽然 dynamic batch loading 只是在剪枝模型再训练阶段提到，但是它也可以运用在 target structed pruning 阶段， 这样剪枝得到的初始模型在每个 domain 的学习程度便已经尽可能和大模型相似了，更有利于后面的再训练。 这里还有一个小问题，初始的 $\omega_0$ 该如何确定？对于 target structed pruning 阶段，则使用数据集 $D^{val}$ 本身的 domain 权重(即数据集 $D^{val}$ 中各个 domain 的数据量)作为 $\omega_0$； 而对于剪枝后的再训练，则使用初始的剪枝模型在数据集 $D^{val}$ 上的原始的各个 domain 的 loss 与参考 loss 的差值的比重作为 $\omega_0$。 除此之外。在参考 loss 的选择中，除了将大模型在每个 domain 的 loss 设为参考 loss，还可以使用 scaling law 所预测的 loss 作为参考 loss。