论文题目：High-Resolution Image Synthesis With Latent Diffusion Models

发表会议：The IEEE / CVF Computer Vision and Pattern Recognition Conference(CVPR 2022)

第一作者：Robin Rombach(LMU(Ludwig Maximilian University) Munich)

Question

如何减少 DM(Diffusion Model) 的 train 计算量和提高 inference 速度，同时保证其生成图像的逼真性，并添加额外的 condition 控制模型生成。

Preliminary

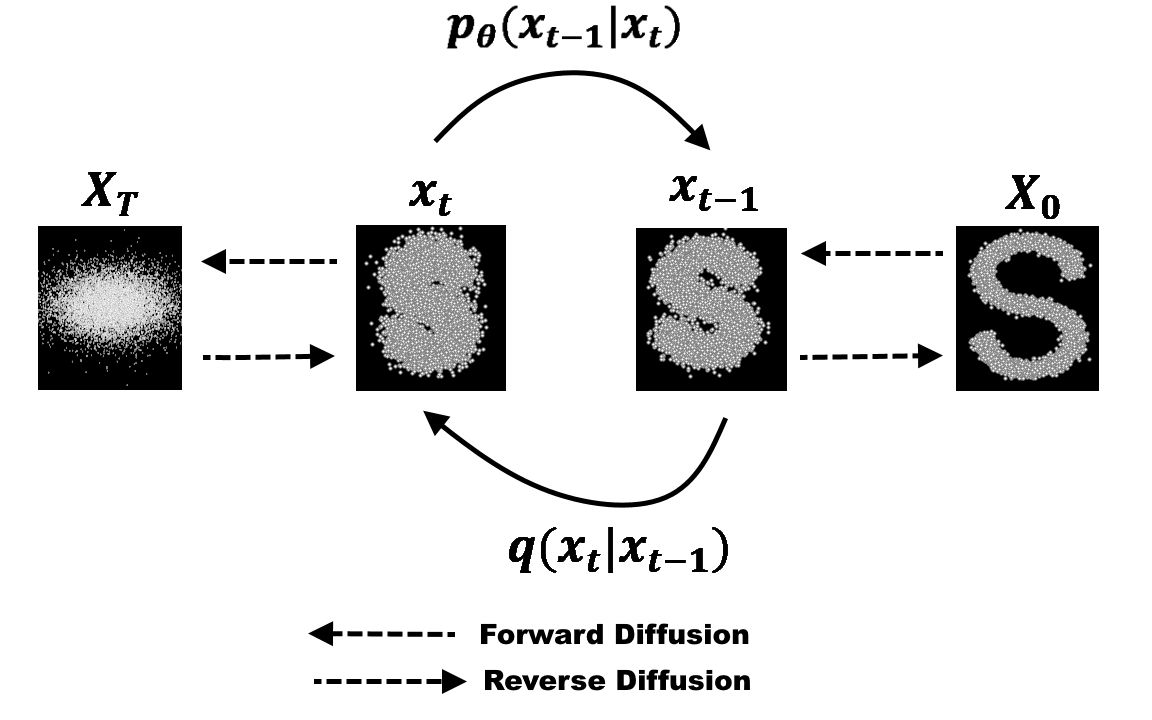
Diffusion Model：扩散模型是近年来最热的图像生成思想。 将任意一张图像 $I_0$ 进行噪声添加，每次添加一个服从 $N(0,1)$ 分布的随机噪声 $\epsilon_t$，获得含有噪声的图像 $I_t$，则进行了无数次后，原本的图像就会变成一个各向同性的随机高斯噪声。 按照这个理论，我们对一个各向同性的随机高斯噪声每次添加一个特定的服从 $N(0,1)$ 分布的噪声 $\epsilon_t'$，获得噪声量减少的图像 $I_t'$，则经过足够多次后便可获得一张逼真的图像 $I_0'$。 为此，我们可以选择任意一个图像生成模型 $M_G$ (例如 U-net 等)，第 t 次时输入第 t-1 次生成的图像 $I_{t-1}'$，输出生成的图像 $I_t'$。 由于每次使用的是同一个图像生成模型 $M_G$，所以需要输入时间步信息 $t$ 来告诉模型现在是生成的第几步 (一个直观的理解是在随机噪声恢复成原始图像的前期，模型更关注图像的整体恢复，而后期则更加关注图像的细节恢复，所以需要时间步信息告诉模型现在是偏前期还是后期)。 同时通过 $I_{t-1}$ 直接生成 $I_t$ 较为困难，因为它需要生成正确其每个像素值，而每次添加的噪声 $\epsilon_t$ 较容易预测。 因此可以更换为每次输入 $I_{t-1}$，模型预测第 $t$ 次所加的噪声 $\epsilon_t$。所以损失函数为 $L = E_{z_0, t, c_t, \epsilon \sim N(0,1)}[||\epsilon - \epsilon_{\theta}(z_t, t, c_t)||_2^2]$。 其中 $z_0$ 是原始噪声(即一开始输入的图像)，而 $z_t$ 是第 $t$ 步输出的图像, $\epsilon_{\theta}(z_t, t, c_t)$ 为模型预测的第 $t$ 步所加的噪声。

Method

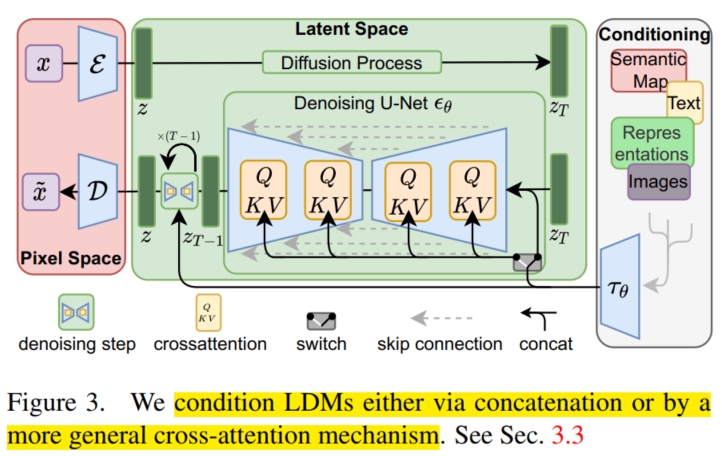
DM 虽然在图像逼真度上已经超过了目前的 SOTA(GAN)，但是之前的 DM 方法都是直接在 pixel 空间上进行的(比如输入一张带噪声的图像，经过 U-net 模型后，输出同样大小的去噪图像)。 这对于生成高分辨率的图像来说计算量是很大的。本文通过观察发现，之前的方法都基本上进行了两阶段的学习：第一阶段是 perceptual compression(感知压缩)，第二阶段是 semantic compression(语义压缩)。 而它们有很大一部分算力都花费在了人们难以察觉的 imperceptible detail 上，即在 perceptual compression 阶段花费的时间和算力过多。 于是作者便想寻找一个 perceptual 信息与原 pixel 空间相似的(即仅仅去除了 imperceptible detail)，而维度更低的空间，在该空间中进行 semantic compression，便可以减少计算量和时间。 具体而言，作者首先训练了一个 autoencoder(自编码器)，使用的损失函数为 perceptual loss $公式1$ 和 patch-based adversarial objective $公式2$。 假设输入的原始图像为 $x \in R^{H \times W \times 3}$， autoencoder 由编码器 $E(·)$ 和解码器 $D(·)$ 组成，编码器 $E(·)$ 将原始图像 $x$ 转化为 latent representation $z \in R^{h \times w \times c}$：$z = E(x)$。 而解码器 $D(·)$ 将 $z$ 重构成原始图像 $\widetilde{x} = D(z) = D(E(x))$。 为了限制 autoencoder 学习到的空间(避免 high-variance)，本文分别实验了两种不同的约束条件：1) $KL-reg$，即引入 KL 散度将模型学习到的 latent 空间尽可能规范到 standard normal(标准正态分布) 和 2) $VQ-reg$ (参考 VQ-VAE)，即将 autoencoder 学习到的空间限制在有限个的 vector 中(Vector Quantization)。

随后，便在 latent 空间($z$ 所在空间)上使用 DM 模型 $\epsilon_{\theta}(·,·)$ 进行正常的扩散模型学习。 具体而言，首先将原始噪声图像 $x$ 经过编码器 $E(x)$ 生成 latent representation $z$。 随后经过 $T$ 步的扩散模型 $\epsilon(z,t)$ 去噪生成不含噪声的 latent representation $z_T$，最后再经过解码器 $D(z_T)$ 生成去噪后的图像 $x_T$。 所以在这一步( Diffusion 步骤)的损失函数和正常的 DM 类似，为 $L_{LDM} := E_{E(x), \epsilon \sim N(0,1), t}[||\epsilon - \epsilon_{\theta}(z_t,t)||_2^2]$。

为了能在该框架下引入条件控制模型的生成，本文引入了 cross-attention 机制来帮助学习。 对于预处理的条件 $y$ (可以是各种模态)，本文使用了特定域的编码器 $\tau_{\theta}$ 将 $y$ 投影到中间表示(intermediate representation)：$\tau_{\theta}(y) \in R^{M \times d_{\tau}}$。 同时也将 latent representation $z_t$ 也投影到中间表示：$\varphi_i(z_t) \in R^{N \times d_{\epsilon}^i}$。 然后通过 cross-attention 层将条件 $y$ 的之间表示 $\tau_{\theta}(y)$ 与 DM 模型(通常是 U-net)的中间层进行交互： $Q = W_Q^{(i)}·\varphi_i(z_t)$, $K = W_K^{(i)}·\tau_{\theta}(y)$, $V = W_V^{(i)}·\tau_{\theta}(y)$, $Attention(Q, K, V) = softmax(\frac{QK^T}{\sqrt{d}})·V$。 最后基于图像-条件对，损失函数为 $L_{LDM} := E_{E(x),y,\epsilon \sim N(0,1),t}[||\epsilon - \epsilon_{\theta}(z_t, t, \tau_{\theta}(y))||_2^2]$。