这篇博客主要介绍了 NLP 任务中的基础知识，包括性能评价指标(metrics)，分词算法(tokenization)等。

Metric

BLEU (BLEU Score)：Bilingual Evaluation Understudy， 主要用于计算一对多的 Translation 的任务的质量，例如 Machine Translation。这种任务通常拥有多个 ground-truth (参考代码)。其计算公式如下：

其中，$\omega_n$ 表示 $n-gram$ 的权重；$Out$ 表示预测的句子 $\hat{y}$，$Ref$ 表示 ground-truth 的句子 $y$；$n-gram$ 表示由 $n$ 个词组成的词组； $Counter_{Clip}(x)$ 表示 $x$ 在 $Ref$ 中出现的次数和在 $Out$ 中出现的次数的最小值； $Counter(x)$ 表示 $x$ 在 $Out$ 中出现的次数；$L_{out/ref}$ 表示 $Out/Ref$ 的长度。

对于整个测试集 $\mathcal{D}_t:\{S_i,y_i\}_{i=1}^{M}$，BLEU 的计算公式如下：

其中，$\{Candidates\} = \{\hat{y}_i\}_{i=1}^M$； $c$ 表示 $\mathcal{D}_t$ 中所有预测的句子 $\hat{y}_i$ 的长度 $L_{out}^i$ 的总和：$c = \sum_{i=1}^ML_{out}^i$， $r$ 表示 $\mathcal{D}_t$ 中所有 ground-truth 的句子 $y_i$ 的长度 $L_{ref}^i$ 的总和：$r = \sum_{i=1}^ML_{ref}^i$ (如果每个 $S_i$ 对应不止一个目标句子 $y_i^j, j=1,...,J$， 则 $L_{ref}^i$ 表示与预测的句子 $\hat{y}_i$ 的长度最短的目标句子 $y_i^j$ 的长度 $L_{ref}^{i,j}$：$\underset{y_i^j, j = [1,...,J]}{arg\ min}{|L_{out}^i - L_{ref}^{i,j}|_1}$)。 BlEU Score 是通过将整个测试/训练/验证集的文本作为一个整体来计算的。因此，不能对集合中的每个句子单独计算 BlEU Score，然后用某种方式平均得到最终的分数。

WER：Word Error Rate，主要用于计算一对一的 Translation 的任务的质量，例如 Speech-to-text。 这种任务通常只有一个 ground-truth (参考代码)。其计算公式如下：

其中，$L_{out}$ 表示预测的句子 $\hat{y}$ 的长度；$d_{Levenstein}$ 表示 Levenstein distance，即编辑距离，表示将预测的句子 $\hat{y}$ 转化为 ground-truth $y$ 所需的编辑步骤。 而所定义的编辑步骤由 $3$ 个部分组成：Insert(i)，表示在第 $i$ 个位置添加一个词；Delete(i)：表示删除第 $i$ 个位置的词； Substitute(i, w)：表示将第 $i$ 个位置上的词换成 $w$。$d_{insert/delete/substitute}$ 分别表示将预测的句子 $\hat{y}$ 转化为 $y$ 所需的 $insert/delete/substitute$ 的次数。 通常情况下，我们不会分开计算 $3$ 个编辑步骤的各自次数， 而是使用 DP (Dynamic Programming， 动态规划)算法直接求解 $d_{Levenstein}$。

ROUGE-L，主要用于计算一对多的 Translation 的任务的质量，例如 Machine Translation。 这种任务通常拥有多个 ground-truth (参考代码)。 具体而言，对于一对一的 Translation 任务，其计算公式如下：

其中，$Y$ 表示预测的句子，$n$ 表示其长度，$X$ 表示对应的 ground-truth，$m$ 表示其长度； $LCS(X, Y)$ 表示序列 $X$ 和 $Y$ 的最长公共子序列的长度；$\beta$ 表示权重：$\beta = \dfrac{P_{lcs}}{R_{lcs}} \leftarrow \dfrac{\partial F_{lcs}}{\partial R_{lcs}} = \dfrac{\partial F_{lcs}}{\partial P_{lcs}}$。 而对于一对多的 Translation 任务，其计算公式如下：

其中，$c$ 表示预测的句子，$n$ 表示其长度，$r_{1,...,u}$ 表示对应的 $u$ 个 ground-truth，$m_j,j=[1,...,u]$ 表示 $r_j$ 的长度； $\beta$ 表示权重，和一对一的 Translation 任务的计算公式相似：$\beta = \dfrac{P_{lcs-multi}}{R_{lcs-multi}} \leftarrow \dfrac{\partial F_{lcs-multi}}{\partial R_{lcs-multi}} = \dfrac{\partial F_{lcs-multi}}{\partial P_{lcs-multi}}$。 最长公共子序列的求解可以使用 DP 算法，时间复杂度为 $O(mn)$。

Tokenization

BPE：Byte Pair Encoding，是一种数据压缩技术(参考代码)： 它使用单个未使用的字节迭代地替换序列中最频繁的字节对。 具体而言，首先使用字符词汇表($26$ 个字母，character vocabulary)初始化符号词汇表(symbol vocabulary)， 并将每个单词(word)表示为字符序列(character seq)，加上一个特殊的词尾符号 “·”，这使能够在翻译后恢复原始标记化，也就是从 subword 恢复成 word。 然后，迭代计算所有符号对(symbol pair)，并用新符号(symbol) “AB” 替换最频繁的对 (’A‘, ’B‘) 的每次出现。每个合并操作都会生成一个表示字符 n-gram 的新符号(symbol)。 最终的符号词汇表内的符号数量等于初始词汇量($26$ 个字母)加上合并操作生成的符号数量(超参数)。 注意，特殊词尾符号 “·” 也进行合成步骤。伪代码算法如下图(其中 '<\w>' 表示词尾符号 ”.“)：

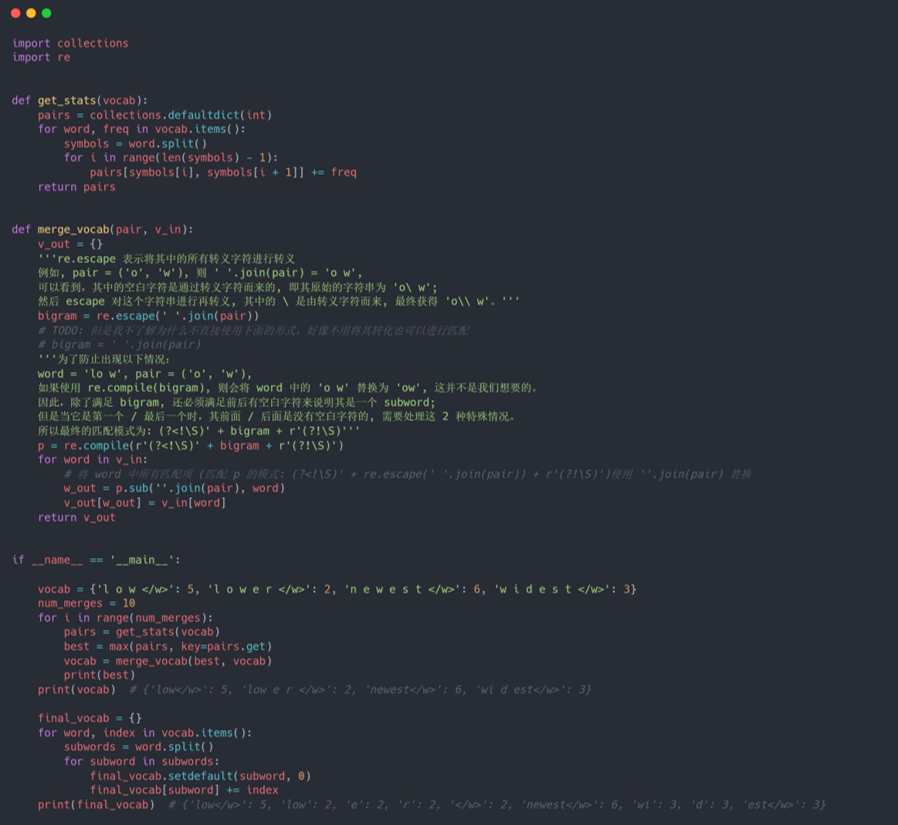
在使用阶段，首先将给定的单词表示为字符序列，然后遍历符号词汇表内的符号(从长到短)， 不断尝试将单词字符序列与符号进行匹配(即将字符序列进行合成)，直到字符序列内的所有字符都已合成为符号词汇表内的符号。 而对于无法使用符号词汇表内的符号进行合成的单词，只需要在现有的符号词汇表上对其再进行一次 BPE 即可。

而在 inference 阶段，需要将模型预测生成的符号转化为原始的单词。 由于前述将词尾符号一同进行合成，这里只需要将所有预测生成的符号序列按预测顺序进行排列， 然后在 $2$ 个词尾符号 ”.“ (即代码中的 '<\w>')之间的即为一个完整的单词(参考资料)。

BBPE：byte-level BPE，将 BPE 扩展到 byte 的层面上(参考代码)。 具体而言，BBPE 将每个字符都使用 UTF-8 进行字节编码(使用 $16$ 进制表示)，然后将每个单词表示为字节序列(byte seq)，然后使用 BPE 以每个字节为符号(symbol)进行迭代编码。 注意，其中特殊词尾符号 “·” 也进行字节编码并参与合成。 而在使用阶段，首先将给定的单词表示为字节序列，然后遍历符号词汇表内的符号(从长到短)， 不断尝试将单词字节序列与符号进行匹配(即将字节序列进行合成)，直到字节序列内的所有字节都已合成为符号词汇表内的符号。 而在 inference 阶段，需要将模型预测生成的符号转化为原始的单词。 由于前述将词尾符号一同进行合成，同时 UTF-8 的字节编码方式具有哈夫曼编码的唯一性(前缀唯一性)，所以转化的过程是唯一的。 这里可以参考 BPE，只需要将所有预测生成的符号序列按预测顺序进行排列，然后找到序列中的每个词尾符号 ”.“ 的字节编码，在 $2$ 个词尾符号 ”.“ 的字节编码之间的即为一个完整的单词的字节编码。 但是该方法的错误率较高，很可能 $2$ 个词尾符号 ”.“ 的字节编码之间的不止一个单词。 由于 UTF-8 的这种字节编码特性，这里可以使用另一种基于递归的方法来实现转化， 具体转化算法如下：对于一个给定的字节编码序列 $\{B\}_{k=1}^N$，定义该序列可转化出的最大字符数量为 $f(k)$ (即 $\{B\}_{k=1}^N$ 一共可以转化为 $f(N)$ 个单词)，可以使用如下 $DP$ 算法进行求解：

其中，如果 $\{B\}_{k=i}^j$ 对应一个合法的字符，则 $g(i,j) = 1$；反之，则 $g(i,j) = 0$。 在每个 $f(k)$ 的计算过程中，可以记录其对于上一个状态的选择(即每个 $f(k)$ 是从哪个状态转移过来的)，这样在转化时，就可以通过回溯来实现。 如果字节编码无法对应一个单词，可以使用纠错码算法进行修正。注意，不是所有的错误字节编码都可以正确修正。

WordPiece，其思想与 BPE 类似， 都是使用单个未使用的字节迭代地替换序列中的字节对。与 BPE 不同的是，WordPiece 选择字节对的标准是最大化似然函数。 具体而言，首先使用字符词汇表($26$ 个字母 + 其他特殊字符，character vocabulary)初始化符号词汇表(symbol vocabulary)， 并使用初始化的符号词汇表对训练数据进行 tokenize，然后使用该数据训练一个语言模型 $P_\theta(·)$。 通过组合当前符号词汇表中的两个符号来生成一个新的符号，使符号词汇表的符号数量加一，将其替换对应的两个符号添加到语言模型时，可以最大程度地增加训练数据上的似然概率： 即假设训练句子为 $S = \{t_1,...,t_n\}$ ($t_i$ 表示符号，$S$ 是已经使用初始化的符号词汇表 tokenize 的)，其语言模型的似然概率 $log\ P(S) = \sum_{i=1}^nlog\ P(t_i)$。 当位置为 $x$ 和 $y=x+1$ 的符号 $t_x$ 和 $t_y$ 进行组合，生成新的符号 $t_{[x:y]} = [t_x, t_y]$ 后， 句子 $S$ 的语言模型的似然概率为：

因此，将 $t_x$ 和 $t_y$ 进行组合后的句子的语言模型的似然概率增值为 $log\ P'(S) - log\ P(S) = log\dfrac{P(t_{[x:y]})}{P(t_x)P(t_y)}$。 通过选择增值最大的符号对进行组合来实现符号词汇表的更新：

重复上述组合步骤直到达到设定的符号词汇表大小或似然概率增量低于某一阈值。

最简单的语言模型 $P_\theta(t)$ 是每个符号 $t$ 的频数概率，即 $P_\theta(t) = \dfrac{freq(t)}{freq(any)}$，其中 $freq(t)$ 表示符号 $t$ 在训练数据 $\mathcal{D}$ 中的出现次数； 而 $freq(any)$ 表示任意词在训练数据中的出现次数，也就是整个数据 $\mathcal{D}$ 的总符号数。 当进行组合时，$P_\theta(t_{[x:y]}) = \dfrac{freq(t_{[x:y]})}{freq(t_x) + freq(t_y) - freq(t_{[x:y]})}$，其中 $freq(t_{[x:y]})$ 表示符号对 $t_{[x:y]}$ 在训练数据 $\mathcal{D}$ 中的出现次数； 而 $freq(t_x) + freq(t_y) - freq(t_{[x:y]})$ 表示训练数据 $\mathcal{D}$ 中任意符号对中一个为 $t_x$ 的出现次数和任意符号对中一个为 $t_y$ 的出现次数减去符号对 $t_{[x:y]}$ 出现次数 (因为符号对 $t_{[x:y]}$ 在任意符号对中一个为 $t_x$ 和任意符号对中一个为 $t_y$ 都统计了一次(一共两次)，因此需要减去一次)。

Unigram：Unigram Language Model (参考代码)。 其思想与 WordPiece 类似，都是使用最大化似然函数迭代更新符号词汇表。与 WordPiece 不同的是，ULM 使用的是从多到少的删减策略。 由 WordPiece 可知，一般似然函数为 $P = (\vec{x}|X) = P(\vec{x}) = \prod_{i=1}^Mp(x_i)$，其中原始句子 $X$ 的分词结果为 $\vec{x} = (x_1,...,x_M)$。 而对于一个预定义的符号词汇表 $V$，可以通过维特比算法计算关于句子 $X$ 最有可能的分词方式：$\vec{x}^* = \underset{x \in S(X)}{arg\ max}P(\vec{x})$， 其中 $S(X)$ 是句子 $X$ 在符号词汇表 $\mathcal{V}$ 下的所有不同分词结果集合。 然后就可以通过 EM 算法来估计 $p(x_i)$，其中 E 步则是使用更新的符号词汇表 $\mathcal{V}$ 来更新每个符号的概率：$p(x_i) = \dfrac{freq(x_i)}{freq(any)}, x_i \in \mathcal{V}$。 而 M 步(Maxmize)是在删除 $\eta$ 比例的符号后，最大化训练数据的所有句子的所有分词组合形成的概率：

具体而言，在 M 步时，首先为每一个符号 $x_i$ 计算 $loss_i = \mathcal{L}_{\mathcal{V}} - \mathcal{L}_{\mathcal{V} - x_i}$， 即 $loss_i$ 代表如果将第 $i$ 个符号去掉，上述似然函数值 $\mathcal{L}$ 的减少量。 然后根据 $loss_i$ 进行排序(由小到大)，保留 $loss$ 最低的 $\eta$ 比例的符号(一般 $\eta = 80%$)。注意，需要保留所有的单字符符号(即 $26$ 个字符 $+$ 特殊字符)，从而避免 $OOV$ 的情况。 最终得到删减后的符号词汇表 $\mathcal{V}' = \mathcal{V} - (1 - \eta)\mathcal{V}$。 但是在刚开始时没有给定的符号词汇表，因此首先需要构建一个足够大的符号词汇表。一般可用训练数据中的所有字符加上常见的子字符串初始化符号词汇表，也可以通过 BPE 算法初始化。 然后，给定一个 Unigram 语言模型 $p(x) = \dfrac{freq(x)}{freq(any)}$，迭代使用上述 EM 算法来优化 $p(x_i), x_i \in \mathcal{V}$ 和 $\mathcal{V}$， 直到最终的符号词汇表 $\mathcal{V}$ 的符号数量达到阈值(参考资料)。 注意：虽然论文原文写的是 "Fixing the set of vocabulary, optimize $p(x)$ with the EM algorithm"， 但是根据参考资料的实现来看，EM 算法是融合在整个符号词汇表 $\mathcal{V}$ 的更新中的。 也就是说，论文第 $3$ 页的算法步骤描述应更改为如下更为恰当：

1. Heuristically make a reasonably big seed vocabulary from the training corpus.

2. Repeat the following steps until $|\mathcal{V}|$ reaches a desired vocabulary size using EM algorithm.

   1. E step: Fixing the set of vocabulary, optimize $p(x)$.

   2. M step: Compute the $loss_i$ for each subword $x_i$, where $loss_i$ represents how likely the likelihood $L$ is reduced when the subword $x_i$ is removed from the current vocabulary. Sort the symbols by lossi and keep top $\eta\%$ of subwords ($\eta$ is $80$, for example). Note that we always keep the subwords consisting of a single character to avoid out-of-vocabulary.