这篇博客参考了 DDPM讲解，详细讲述了最近大火的 DM 模型的数学原理/推导及编程(ps：强烈安利 Lil 的博客，写的太好了🙂)。

DM的基本原理

DM 的思想如下：往一张图像中一点一点地加噪声，经过无限次之后，它将变成一个各向同性的标准正态分布噪声，这个过程叫做扩散过程。 那么将这个过程进行反转，往一个各向同性的标准正态分布噪声中一点一点地加上特定的噪声(即加上扩散过程每一步噪声的相反数)，那么经过无限次之后， 它就会变回到原始的图像，这个过程叫做逆扩散过程。

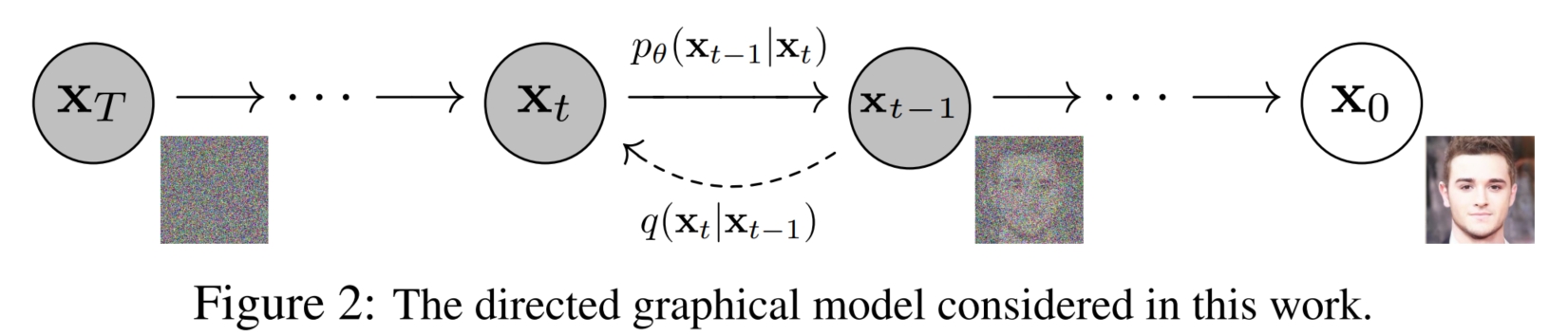
具体而言，假设扩散过程的第 $t$ 步的噪声为 $d_t \in \mathcal{N}(0, \beta_t\boldsymbol{I})$， 扩散之前的图像为 $x_{t-1}$，扩散之后的图像为 $x_{t}$，$x_{t}$ 在已知 $x_{t-1}$ 下的条件概率为 $q(x_t|x_{t-1})$。则

即 $x_{t}^2 \Rightarrow (\sqrt{1-\beta_t}x_{t-1})^2 + {d_t}^2 \Rightarrow (\sqrt{1-\beta_t}x_{t-1})^2 + ({\sqrt{\beta_t}\varepsilon_t})^2$。 所以，我们需要提前设置一组方差序列 $\{\beta_{t} \in (0, 1)\}_{t=1}^T$，方差越小则表示噪声扰动越小，对图像的影响也越小。 因为我们生成图像是逆扩散过程，即 $t\ from\ T\ to\ 1$，我们希望模型在初期时(即 $t \approx T$)能够尽量恢复图像的大体轮廓， 所以这时期的每一步之间的图像变化要大一些，即 $\beta_t$ 要大一些；而在后期时(即 $t \approx 1$)，模型能够尽量恢复图像的细节部分， 所以这时期的每一步之间的图像变化要小一点，即 $\beta_t$ 要小一点，因此，方差序列的大致大小为 $\beta_1 < ... < \beta_T$。

有了扩散过程的公式，逆扩散过程的公式便是将其反转，即我们在已知扩散之后的图像为 $x_{t}$，需要预测扩散之前的图像 $x_{t-1}$， 则 $x_{t-1}$ 在已知 $x_{t}$ 下的条件概率为 $q(x_{t-1}|x_t) \Rightarrow x_{t-1} = \dfrac{(x_t - \sqrt{\beta_t}\varepsilon_{t-1})}{\sqrt{1 - \beta_t}}$， 注意，这里的 $\varepsilon_t$ 是一个确定的数，即扩散过程时添加的 $\varepsilon_t$。 因此，我们只需设计一个模型，使得其输入 $x_t$，输出 $\varepsilon_{\theta}$，并训练它学习使得 $\varepsilon_{\theta} \approx \varepsilon_t$，即最终能够预测出每一步的噪声。 然后我们通过逆扩散公式 $\hat{x}_{t-1} = \dfrac{(x_t - \sqrt{\beta_t}\varepsilon_{\theta})}{\sqrt{1 - \beta_t}}$ 即可获得预测的 $\hat{x}_{t-1}$。

注意：$\beta_{t}, t = 1,...,T$ 对于每一个 $x_0$ 都是固定的；但是 $\varepsilon_t, t = 1,...,T$ 对每个 $x_0$ 都是不固定的，随机采样的。 这就导致你想训练数据 $x_t^i \rightarrow x_{t-1}^i$ 时，你只能先扩散 $t$ 步，得到 $\varepsilon_{1:t}^i$，然后才能进行逆扩散过程训练。 假设你有 $1B$ 数据，$T$ 通常取 $1000$，为了确保 $1\sim T$ 的每个逆扩散过程都可以充分学习，需要获得每个数据的 $\varepsilon_{1:T}$。 也就是在还没开始训练时，准备好训练数据就要计算(扩散) $1B \times 1000$ 次，而且还得存储 $1B \times 1000$ 个 $\varepsilon_t^i$ 的数据，这个代价是很大的。 这也是虽然 DM 思想很早以前就存在，但是却一直没有人使用的原因(当然还有一部分原因是效果不好)。

而 DM 的第一个改进(由 DDPM 论文提出)是，你不需要中间繁琐的 $\varepsilon_{1:t}$， 而是用一个 $\bar{\varepsilon}_0$ 就可以通过一步扩散从 $x_0^i$ 到 $x_t^i$，即直接获得 $q(x_t^i|x_0^i)$。 这时你需要训练数据 $x_0^i$ 的 $x_t^i \rightarrow x_{t-1}^i$ 时，不需要 $t$ 步扩散得到 $x_t^i$，而是一步扩散就可以得到 $x_t^i$。 因此在训练时你也不需要存储 $1B \times 1000$ 个 $\varepsilon_t^i$ 的数据， 想训练 $x_t^i \rightarrow x_{t-1}^i$，就直接现场采样 $\bar{\varepsilon}_0$ 并加到 $x_0^i$ 上，就可以获得 $x_t^i$。

那么如何确定这个 $\bar{\varepsilon}_0$ 呢？回看扩散过程，$x_t = \sqrt{1 - \beta_t}x_{t-1} + \sqrt{\beta_t}\varepsilon_{t-1}$， 通过将左边的 $x_{t-1}$ 使用 $x_{t-2}$ 展开，直到 $x_0$，就得到了 $q(x_t|x_0)$ 的表达式。 那么这个表达式里面可以经过化简合并，变成仅包含一个随机变量 $\bar{\varepsilon}_0$ 吗？ 不一定，因为不是所有的概率分布，都可以将任意的 $t$ 随机变量 $\varepsilon_{1:t}$ 融合成一个随机变量 $\bar{\varepsilon}_0$， 但幸运的是，$\varepsilon_{1:t} \sim \mathcal{N}(0, \boldsymbol{I})$。 正态分布，是我见过的最奇妙的概率分布，无论是多个随机变量的加法还是乘法，都可以融合成一个随机变量。 这也是为什么扩散模型使用的都是正态分布，而不是其他分布，不仅仅是因为它的常见性，还有它的数学特性，可以帮助简化模型学习。

递推式的展开过程如下：为了方便表示，令 $\alpha_t = 1 - \beta_t$，$\bar{\alpha}_t = \prod_{i=1}^t{\alpha_i}$。 则 $x_t = \sqrt{\alpha_t}x_{t-1} + \sqrt{1 - \alpha_t}\varepsilon_{t-1}$， 代入 $x_{t-1} = \sqrt{\alpha_{t-1}}x_{t-2} + \sqrt{1 - \alpha_{t-1}}\varepsilon_{t-2}$ 得：

其中，$\sqrt{\alpha_t - \alpha_t\alpha_{t-1}}\varepsilon_{t-2} \sim \mathcal{N}(0, (\alpha_t - \alpha_t\alpha_{t-1})\boldsymbol{I})$，$\sqrt{1 - \alpha_t}\varepsilon_{t-1} \sim \mathcal{N}(0, (1 - \alpha_t)\boldsymbol{I})$，所以 $\sqrt{\alpha_t - \alpha_t\alpha_{t-1}}\varepsilon_{t-2} + \sqrt{1 - \alpha_t}\varepsilon_{t-1} \sim \mathcal{N}(0, (1 - \alpha_t\alpha_{t-1})\boldsymbol{I})$ 也是一个正态分布，用 $\bar{\varepsilon}_{t-2} \sim \mathcal{N}(0, \boldsymbol{I})$ 表示可得

经过不断展开，最终可得 $x_t = \sqrt{\bar{\alpha}_t}x_0 + \sqrt{1 - \bar{\alpha}_t}\bar{\varepsilon}_0, \bar{\varepsilon}_0 \sim \mathcal{N}(0, \boldsymbol{I})$，即 $q(x_t|x_0) = \mathcal{N}(x_t; \sqrt{\bar{\alpha}_t}x_0,(1 - \bar{\alpha}_t)\boldsymbol{I})$

由于 $\beta_{t}, t = 1,...,T$ 是固定的，所以我们可以先计算出每个 $\bar{\alpha}_t$，然后对于需要任意的 $t$ 步扩散数据，只需要现场采样一个 $\bar{\varepsilon}_0$，就可以获得 $x_t$：$x_t = \sqrt{\bar{\alpha}_t}x_0 + \sqrt{1 - \bar{\alpha}_t}\bar{\varepsilon}_0$

接下来还有一个问题，我们是逆扩散 $x_t \rightarrow x_{t-1}$，预测结果为 $\varepsilon_t$，而不是 $\bar{\varepsilon}_0$，因此还需要进一步将模型转化到预测 $\bar{\varepsilon}_0$。 再回看 $q(x_{t-1}|x_t)$，因为 $x_{t-1}$ 与 $x_0$ 无关，所以可以写成 $q(x_{t-1}|x_t,x_0)$，通过贝叶斯公式分解可得

其中，$q(x_t|x_{t-1}) = \mathcal{N}(x_t; \sqrt{1-\beta_t}x_{t-1},\beta_t\boldsymbol{I}) \Rightarrow x_t = \sqrt{1 - \beta_t}x_{t-1} + \sqrt{\beta_t}\varepsilon_{t-1}$，$q(x_{t-1}|x_0) = \mathcal{N}(x_{t-1}; \sqrt{\bar{\alpha}_{t-1}}x_0,(1 - \bar{\alpha}_{t-1})\boldsymbol{I})$，$q(x_t|x_0) = \mathcal{N}(x_t; \sqrt{\bar{\alpha}_t}x_0,(1 - \bar{\alpha}_t)\boldsymbol{I})$

然后，通过正态分布的概率密度函数 $\mathcal{N}(\mu, \sigma) = \dfrac{1}{\sqrt{2\pi}\sigma}exp(-\dfrac{(x-\mu)^2}{2\sigma^2})$， 对上式进行进一步化简可得(推导见附录 $A$)：

将 $x_t = \sqrt{\bar{\alpha}_t}x_0 + \sqrt{1 - \bar{\alpha}_t}\bar{\varepsilon}_0 \Rightarrow x_0 = \dfrac{1}{\sqrt{\bar{\alpha}_t}}(x_t - \sqrt{1 - \bar{\alpha}_t}\bar{\varepsilon}_0)$ 代入 $\tilde{\mu}_t(x_t,x_0)$ 可得：

此时，$q(x_{t-1}|x_t)$ 就只依赖 $x_t$ 和 $\bar{\varepsilon}_0$，即

因此，我们只需要设计一个模型 $\varepsilon_{\theta}(x_t,t)$ 来通过输入 $x_t$ 和 $t$ 来预测添加的噪声 $\bar{\varepsilon}_0$，并使用 $MSE\ loss$ 计算损失,就可以实现模型训练：

在获得了 $\bar{\varepsilon}_0$ 后，想要通过 $\bar{\varepsilon}_0$ 和 $x_t$ 获得 $x_{t-1}$，可以根据

得到 $x_{t-1} = \dfrac{1}{\sqrt{\alpha_t}}(x_t - \dfrac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}}\bar{\varepsilon}_0) + \dfrac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \beta_t \times z_t, z_t \in \mathcal{N}(0, \boldsymbol{I})$。 所以，和直觉不同，在预测得到 $\bar{\varepsilon}_0$ 后，获得 $x_{t-1}$ 仍然需要一次随机采样， 这就导致预测得到的 $\hat{x}_{t-1}$ 和原始的 $x_{t-1}$ 不完全一致，受 $z_t$ 的随机性影响。这是一个不好的结果？ 恰恰相反，这才是让 DM 模型比 GAN 模型多样性强的原因。因为每次随机的不同 $z_t$，导致 DM 模型即使是输入相同的原始各向同性的标准正态分布噪声，也会获得不同的图像，即保证了生成的图像的多样性。 同时，由于有原始的 $x_{t-1}$ 作为指导，使得每次预测的结果都和 $x^{t-1}$ 较为接近，即保证了生成的图像的逼真性。

此外，由于 $x_0 = \dfrac{1}{\sqrt{\bar{\alpha}_t}}(x_t - \sqrt{1 - \bar{\alpha}_t}\bar{\varepsilon}_0)$，理论上也可以根据预测得到的 $\bar{\varepsilon}_0$，直接一步逆扩散到 $x_0$，但是没人这么做，说明效果很差，所以 DDPM 只在输入时使用一步扩散，而在预测时还是使用 $T$ 步的逆扩散。

附录

A. $q(x_{t-1}\vert x_t,x_0)$ 使用正态分布概率密度函数推导：

B. 代码框架：在训练时，首先，你需要预设置方差序列 $\{\beta_{t} \in (0, 1)\}_{t=1}^T$ 并计算 $\bar{\alpha}_{1:T}$。 然后，在 $1\sim T$ 中随机选择一个数字 $t$，并使用正态分布随机函数生成 $\bar{\varepsilon}_0$ (注意，这里生成的正态分布随机变量 $\bar{\varepsilon}_0$ 的维度为 $H \times W \times 3$，和原始图像 $x_0$ 一致)； 通过公式 $x_t = \sqrt{\bar{\alpha}_t}x_0 + \sqrt{1 - \bar{\alpha}_t}\bar{\varepsilon}_0$ 计算 $x_t$，其维度也为 $H \times W \times 3$； 接着构造一个模型，输入 $x_t$ 和 $t$ (通常 $t$ 需要转化成 embedding，类似 Transformer，可以选择正弦函数这种确定的方式，也可以选择 learnable embedding parameter 让模型学习)， 输出和图像 $x_t$ 维度相同的噪声 $\varepsilon_\theta(x_t,t)$，因此一般选择 U-net 架构模型。 最后计算 $MSE$ 损失进行训练：$L_\theta = E_{t \in [1,T],x_0,\bar{\varepsilon}_0}[||\bar{\varepsilon}_0 - \varepsilon_\theta( \sqrt{\bar{\alpha}_t}x_0 + \sqrt{1 - \bar{\alpha}_t}\bar{\varepsilon}_0, t||^2]$。

而在推理时，首先使用正态分布随机函数生成 $\hat{x}_T$，维度为 $H \times W \times 3$，然后 将 $t=T$ 一起输入训练好的模型，预测输出 $\hat{\varepsilon}_0$，并使用正态分布随机函数生成 $z_t$，维度为 $H \times W \times 3$， 接着使用公式 $\hat{x}_{t-1} = \dfrac{1}{\sqrt{\alpha_t}}(x_t - \dfrac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}}\hat{\varepsilon}_0) + \dfrac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \beta_t \times z_t$ 生成预测的 $\hat{x}_{T-1}$，循环迭代，直到 $t = 0$ 时结束，最终的 $\hat{x}_0$ 即为模型生成的图像。下图展示了模型的训练的推理过程：