论文题目：Consistency Models

发表会议：International Conference on Machine Learning (ICML 2023)

第一作者：Yang Song (OpenAI)

Question

如何提高图像生成模型的生成速度，同时尽可能保持高性能(逼真)

Preliminary

Diffusion Model (DM dispersed)：扩散模型是近年来最热的图像生成思想。 将任意一张图像 $I_0$ 进行噪声添加，每次添加一个服从 $N(0,1)$ 分布的随机噪声 $\epsilon_t$，获得含有噪声的图像 $I_t$，则进行了无数次后，原本的图像就会变成一个各向同性的随机高斯噪声。 按照这个理论，我们对一个各向同性的随机高斯噪声每次添加一个特定的服从 $N(0,1)$ 分布的噪声 $\epsilon_t'$，获得噪声量减少的图像 $I_t'$，则经过足够多次后便可获得一张逼真的图像 $I_0'$。 为此，我们可以选择任意一个图像生成模型 $M_G$ (例如 U-net 等)，第 t 次时输入第 t-1 次生成的图像 $I_{t-1}'$，输出生成的图像 $I_t'$。 由于每次使用的是同一个图像生成模型 $M_G$，所以需要输入时间步信息 $t$ 来告诉模型现在是生成的第几步 (一个直观的理解是在随机噪声恢复成原始图像的前期，模型更关注图像的整体恢复，而后期则更加关注图像的细节恢复，所以需要时间步信息告诉模型现在是偏前期还是后期)。 同时通过 $I_{t-1}$ 直接生成 $I_t$ 较为困难，因为它需要生成正确其每个像素值，而每次添加的噪声 $\epsilon_t$ 较容易预测。 因此可以更换为每次输入 $I_{t-1}$，模型预测第 $t$ 次所加的噪声 $\epsilon_t$。所以损失函数为 $L = E_{z_0, t, c_t, \epsilon \sim N(0,1)}[||\epsilon - \epsilon_{\theta}(z_t, t, c_t)||_2^2]$。 其中 $z_0$ 是原始噪声(即一开始输入的图像)，而 $z_t$ 是第 $t$ 步输出的图像, $\epsilon_{\theta}(z_t, t, c_t)$ 为模型预测的第 $t$ 步所加的噪声。 更加详细的介绍推理可以参考 The Basic Knowledge of Diffusion Model (DM)。

Diffusion Model (DM continuous)：如下图(Figure 1)，也被称为 Score-based Generative Model。是 DM 模型的另一种推理方式，可以将噪声推广到连续时间。 详细的介绍推理可以参考 The Basic Knowledge of Scored-based Generative Model。

Method

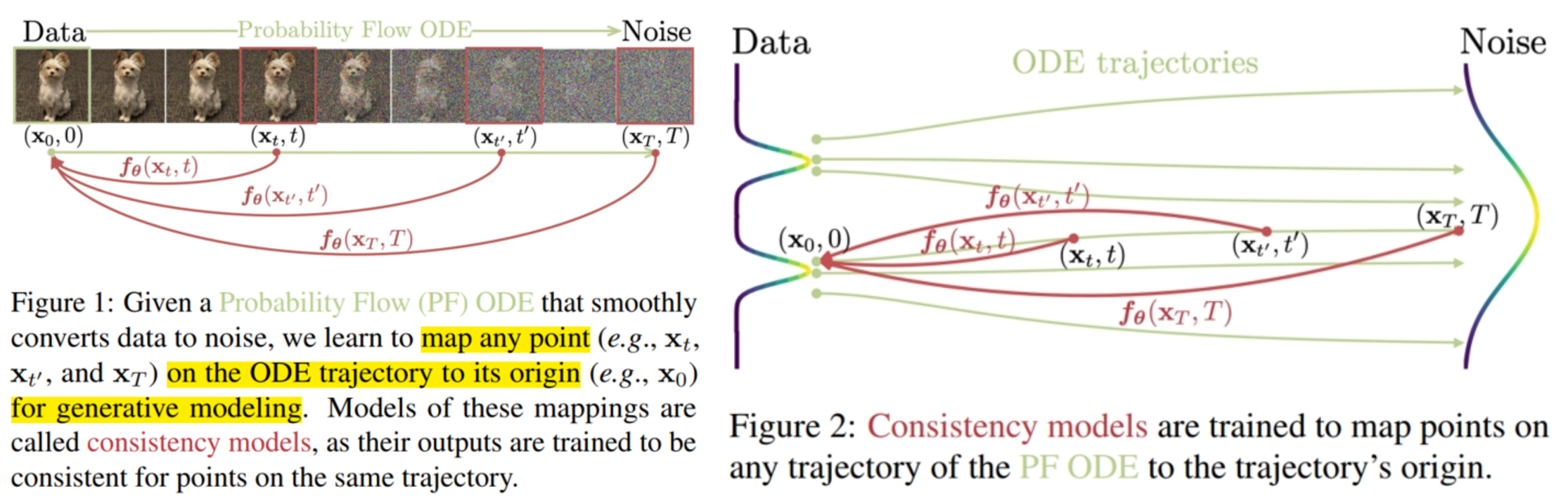
目前 DM 模型最大的不足还是推理的速度太慢，由于需要进行多次逆扩散过程的迭代(即 multi-inference)，导致其推理时间较长。 本文便想构造方法实现一次 inference 直接生成图像。 最直观的方式是设计一个模型(如 U-net) $M_\theta$，输入给定的初始化噪声图像 $x_T$，输出预测的原始图像 $\hat{x}_0$，并使用 ground-truth $x_0$ 作为监督信号， 利用 MSE 函数计算损失 $L_{\theta} = \boldsymbol{E}[||\hat{x}_0 - x_0||_2^2]$ 进行训练。 当然，也可以和 The Basic Knowledge of Diffusion Model (DM) 中提到的一样， 预测出 $x_T$ 所加的噪声 $\bar{\varepsilon_T}$ 来获得原始图像 $\hat{x}_0 = \dfrac{1}{\sqrt{\bar{\alpha}_T}}(x_T - \sqrt{1 - \bar{\alpha}_T}\bar{\varepsilon}_T)$。 但是这 $2$ 种方法的最大缺陷是性能不足，生成的图像的逼真度不够。 其中很大一部分原因是因为在没有其他条件的帮助下，直接让模型建模 $\mathcal{p}(x_0|x_T)/\mathcal{p}(\varepsilon_T|x_T)$ 的难度太大。 为此本文提出通过使用 probability flow (PF) ordinary differential equation (ODE) (概率流常微分方程) 的解轨迹(solution trajectory)来帮助模型学习。

如上图(Figure 1)，DM (continuous) 模型扩散步骤的数学过程是一个 stochastic differential equation (SDE，随机微分方程)：

其中，$\mu(x_t,t)$ 称为 drift coefficient，$\sigma(t)$ 称为 diffusion coefficient， $\{w_t\}_{t \in [0,T]}$ 是 standard Brownain motion (标准布朗运动)，上述方程表示加噪过程。 假设 $x_t$ 的概率分布为 $\mathcal{p}_t(x) \Rightarrow p_0(x) = p_{data}(x), p_T(x) = \pi(x)$。 SDE 有一个重要的性质：即它存在一个 ODE 形式的去噪方程，称为 PF ODE (PF ODE 和 reversal SDE 相对应，即加噪的逆过程)， 而 PF ODE 的解轨迹 $\{x_t\}_{t \in [0, T]}$ 就是将一个噪声图像 $x_T$ 不断去噪后得到的不同程度的去噪图像，最终的 $x_0$ 则是完全去噪后的图像。 在本文的 DM 模型中，其 SDE 所对应 PF ODE 方程如下：

其中，$\triangledown log\ \mathcal{p}_t(x_t)$ 是 $\mathcal{p}_t(x_t)$ 的 score function。 为了方便建模，本文将方程进行简化：令 $\mu(x_t,t) = 0,\ \sigma(t) = \sqrt{2t}$，则 $p_t(x) = p_{data}(x) \otimes \mathcal{N}(0, T^2\boldsymbol{I})$，$\otimes$ 表示卷积。 为了实现对 PF ODE 解轨迹的求解，本文首先通过 score match 方法训练一个 score model $s_{\phi}(x_t,t) \approx \triangledown log\ p_t(x_t)$。 然后将其代入 PE ODE 方程，将方程简化为常系数微分方程(称为 empirical PF ODE)：

然后，采样 $\hat{x}_T \sim \pi = \mathcal{N}(0,T^2\boldsymbol{I})$ 初始化方程， 然后使用 numerical ODE solver (数值常微分方程求解器，例如 Euler/Heun solver)求解方程，从而获得整个解轨迹 $\{\hat{x}_t\}_{t \in [0,T]}$， 其中 $\hat{x}_0$ 可以近似为在数据分布 $\mathcal{p}_{data}(x)$ 中的采样。 为了数值稳定性，通常当 $t = \epsilon, \epsilon \in R^+\ and\ \epsilon \rightarrow 0$ 时就停止计算，并将最终的 $\hat{x}_\epsilon$ 作为 $\hat{x}_0$ 的近似， 则整个解轨迹就变成 $\{\hat{x}_t\}_{t \in [\epsilon,T]}$。本文中使用 $T = 80, \epsilon = 0.002$。

有了解轨迹，本文便提出了 consistency model 来利用它进行一步 inference 的学习。 具体而言，定义 consistency model 为 $\boldsymbol{f_\theta}:(x_t,t) \mapsto x_\epsilon$，即它将解轨迹上的任意一个数据点都映射到原始图像。 从定义可以看出，它具有 self-consistency (自一致)的性质： 即 $\boldsymbol{f_\theta}(x_t,t) = \boldsymbol{f_\theta}(x_{t'},t'), \forall t,t' \in [\epsilon, T]$ (对于任意在相同 PF ODE 解轨迹上的输入对 $(x_t,t)$，其输出一致，都是 $x_\epsilon$)。 为了实现这一性质，就需要对模型进行一定的限制(包括结构、输入输出维度等)。 其中最主要的限制便是 boundary condition：$\boldsymbol{f_\theta}(x_\epsilon,\epsilon) = x_\epsilon$， 即 $\boldsymbol{f_\theta}(·,\epsilon)$ 是一个 identity function (恒等函数)。 这对方法设计是不利的(因为不能自由设计模型来提高性能)，为了尽可能减少对模型的限制(包括输入输出，结构等)，本文提出 $2$ 种方法来构建 consistency model，称为 parameterization (参数化)， 使得能尽可能自由地设计模型：

其中，$F_\theta(x,t)$ 是 free-form 的深度神经网络(即无限制的模型)； 第 $2$ 种方法的 $c_{skip}(t)$ 和 $c_{out}(t)$ 都是可微函数(differentiable)，且满足 $c_{skip}(\epsilon)=1, c_{out}(\epsilon)=0$。 由于第 $2$ 种方法和 DM 模型相似(DM 模型是将噪声 $\varepsilon$ 分离出来实现参数化，即 $f_\theta(x) = x + \varepsilon_\theta(x)$，从而实现模型设计的自由)， 许多流行的 DM 模型架构都可以直接使用，因此本文选择第 $2$ 种方法参数化模型。

而在训练完成后(训练方法下面讲述)，模型可以进行一步 inference 实现图像生成。 具体而言，给定一个训练好的 consistency model $\boldsymbol{f_\theta}(·,·)$，从高斯分布空间中随机采样一个噪声 $\hat{x}_T \sim \mathcal{N}(0,T^2\boldsymbol{I})$， 然后通过模型生成最终的图像 $\hat{x}_\epsilon = \boldsymbol{f_\theta}(\hat{x}_T,T)$。 更重要的是，模型也可以进行多步 inference 利用更多的计算量来提高图像的生成质量(保留了 DM 模型的采样方式)。 它通过多次交替去噪(denoise)和噪声注入(noise)步骤来使用 consistence model 精细化图像。具体算法如下图(Algorithm 1)： 具体而言，给定训练好的模型 $f_\theta(·,·)$，时间点序列 $\tau_1 > ... > \tau_{N-1}$ (类似与 DM 模型的迭代时间 $t$，只是这里的 $\tau \in \mathbb{R}^+$ 是连续时间上的实数)。 首先初始化图像为高斯噪声 $\hat{x}_T \sim \mathcal{N}(0,T^2\boldsymbol{I})$；然后使用模型 $f_\theta(·,·)$ 生成预测的原始图像 $x:x \leftarrow f_\theta(\hat{x}_T,T)$。 接着，循环 $\tau_n$ (n 从 $N-1$ 到 $1$)：每一次循环时，首先采样一个高斯噪声 $z \sim \mathcal{N}(0,I)$， 然后将预测得到的原始图像 $x$ 进行加噪 $\hat{x}_{\tau_n} \leftarrow x + \sqrt{\tau_n^2 - \epsilon^2}z$，获得不同程度的加噪图像 $\hat{x}_{\tau_n}$， 并对该加噪图像使用模型 $f_\theta(·,·)$ 生成进一步预测的原始图像 $x:x \leftarrow f_\theta(\hat{x}_{\tau_n},\tau_n)$。 将优化后的原始图像 $x$ 代入下一次循环进行进一步优化，最终得到预测的原始图像 $x$。

接下来便是模型架构和训练问题。对于模型架构，如前述，本文已经将 consistency model 进行参数化，其中的 $F_\theta(x,t)$ 可以使用任意的主流 DM 模型(如 U-net)； 而对于 $c_{skip}(t)$ 和 $c_{out}(t)$，满足 $c_{skip}(\epsilon)=1, c_{out}(\epsilon)=0$ 的函数也有很多，本文遵循 EDM 推荐的方式，使用：

这样便设计好了模型架构。而对于训练问题，本文提出了 $2$ 种训练方法，使用不同方式估计得到的 PE ODE 解轨迹来帮助模型学习。 第一种是 Distillation，它通过 distill 一个预训练好的 score model $s_\phi(x,t)$ 来训练 consistency model。 回顾上述的讲解，PE ODE 的解轨迹求解需要通过 score match 训练一个 score model $s_{\phi}(x_t,t)$。本文便使用了一个已经训练好的 $s_{\phi}(x_t,t)$ 来求解解轨迹。 具体而言，首先将区间(time horizon) $[\epsilon, T]$ 划分为 $N - 1$ 个子区间：

然后将 $s_{\phi}(x_t,t)$ 代入 empirical PE ODE 方程，并使用 numerical ODE solver 求解 empirical PF ODE，得到 $\hat{x}^{\phi}_{t_n}$：

其中 $\Phi(...; \phi)$ 表示 ODE solver 的更新函数(update function)。例如，如果使用 Euler solver，$\Phi(x,t; \phi)) = -ts_\phi(x,t)$。 在得到解轨迹后，最简单直观的方式是将每个解轨迹的数据点 $\hat{x}^{\phi}_{t_n}$ 都作为输入，使得模型 $f_\theta(\hat{x}^{\phi}_{t_n}, t_n)$ 预测出原始图像 $\hat{x}_0$， 然后使用 MSE 损失进行训练：$L_{\theta} = \boldsymbol{E}[||\hat{x}_0 - x_0||_2^2]$。但是正如上述讨论的，这样的效果并不好。 因此，本文提出使用对比学习的方式来训练模型。我们已经获得了解轨迹 $\hat{x}^{\phi}_{t_n}$，这是训练好的 score function $s_{\phi}(x_t,t)$ 给出的预测轨迹。 同时，由于前述 SDE 和 PF ODE 的关联性，我们也可以通过先采样 $x \sim \mathcal{p}_{data}$，然后向 $x$ 添加高斯噪声，接着沿着 ODE 轨迹的分布进行采样，获得 groudn-truth 的轨迹。 这样我们就可以得到 {预测轨迹点，ground-truth 轨迹点}的数据对。 因为预测轨迹点是由训练好的 score function $s_{\phi}(x_t,t)$ 给出的，它代表了 $s_{\phi}(x_t,t)$ 的性能(即轨迹点的质量)，而 ground-truth 轨迹点则是真实的数据，其质量自然十分好。 通过对这两轨迹点的对比学习，我们就可以 distill $s_{\phi}(x_t,t)$ 的性能，并将其转化到 consistency model 上。 具体算法如下图(Algorithm 2)：具体而言，给定 $x$，首先使用 SDE 的过渡密度分布 $\mathcal{N}(x,t^2_{n+1}\boldsymbol{I})$ 采样得到 $x_{t_{n+1}}$； 然后使用 numerical ODE solver 计算 $\hat{x}^{\phi}_{t_n}$， 与 $x_{t_{n+1}}$ 组成 adjacent data points $(\hat{x}^{\phi}_{t_n}, x_{t_{n+1}})$。 最后，通过最小化数据对 $(\hat{x}^{\phi}_{t_n}, x_{t_{n+1}})$ 的输出差异性(consistency distillation loss)来训练 consistency model：

其中，$\lambda(·) \in R^+$ 表示正值权重函数；$\boldsymbol{\theta}^-$ 表示 $\boldsymbol{\theta}$ 的 EMA (指数移动平均)：

$d(·,·)$ 表示度量函数，满足 $\forall x,y: d(x,y) \geq 0$ and $d(x,y)=0$ if and only if $x=y$。 本文使用 $\lambda(t_n) \equiv 1$，$d(x,y) = \mathcal{l}_2:||x-y||_2^2/\mathcal{l}_1:||x-y||_1/LPIPS$。

第二种是 Isolation，即不需要任何额外的预训练模型，从头开始训练。具体算法如下图(Algorithm 3)：具体而言，回顾上述的 Distillation， 它将预训练好的 score model 近似为 $\triangledown log\ \mathcal{p}_t(x_t)$ 来求解 PE ODE 的解轨迹，进而进行 consistency model 的训练学习。 而想要实现 PE ODE 的解轨迹的求解，并不一定需要训练一个 score model， 我们只需要找到一个不依赖 $s_{\phi}(x,t)$ 的 $\triangledown log\ \mathcal{p}_t(x_t)$ 函数即可，从而进一步实现 Isolation 训练。 为此，本文找到了一个 unbiased estimator (无偏估计器) $\triangledown log\ \mathcal{p}_t(x_t) = -E[\dfrac{x_t-x}{t^2}|x_t], x \sim p_{data}, x_t \sim \mathcal{N}(x;t^2I)$， 然后便可使用相似的 consistency training loss 来训练 consistency model：

其中，$z \sim \mathcal{N}(0,\boldsymbol{I})$。可以看到，使用无偏估计器得到的解轨迹点 $\hat{x}^{\phi}_{t_n}$ 其实就是 ground-truth 轨迹点 $x + t_nz$。 也就是 Isolation 的训练方式是使用不同时刻的 ground-truth 轨迹点进行自我对比学习。

总结，Consistency Model 其实比较简单，假设 DM 模型的扩散过程形成的所有样本为 $x_{1:T}$， Cosistency Model 的目标是将它们一一映射到原始样本 $x_0$：$f_\theta(x_t,t) = x_0$。 但是，直接使用 MSE 损失效果不佳，本文便采样对比学习的损失来训练模型：$L_\theta = E[\lambda(t_n)d(\boldsymbol{f_\theta}(x_{t}, t), \boldsymbol{f_\theta^-}(x_{t-1},t-1))]$。 同时，通过强制性满足 boundary condition 限制保证模型的收敛：$f_\theta(x_0, 0) = x_0$ (不然对比学习可能不能按照 $x_{T:1}$ 的顺序收敛，也有可能按照 $x_{1:T}$ 的顺序收敛，即输入 $x_0$ 时输出 $x_T$)。 同时通过不同的 $x_{t-1}$ 的选择方式(ground-truth 还是预训练模型的预测)来实现不同的训练模式。

附录

1. 仔细观察两个训练的损失函数就可以发现，模型在训练时只考虑了正样本之间的相似性，并没有构造负样本来计算它们的相似性。 为什么本文使用对比学习仅仅考虑了正样本之间的相似性增大，而没有考虑负样本之间的相似性减小，却不会出现模型坍塌问题(即对于任意的输入 $(x_t, t)$)，模型都输出一个相同的数据(比如全 0 矩阵)？ 因为 consistency model 很关键的 boundary condition 限制。从上述可以看到，本文将 boundary condition 限制视为一个硬性限制，并使用模型上的设计来实现。 这样一来，当输入 $x = x_\epsilon^i$ ($i$ 表示第 $i$ 个训练数据)时，$f_\theta(x_\epsilon^i, \epsilon)$ 就必须强制输出 $x_\epsilon^i$， 这样模型就无法通过简单地输出任意相同的数据来实现“捷径”，即不会发生模型坍塌。这就是为什么论文会说 boundary condition 限制是最重要的一个限制。

2. 本文是使用 $\hat{x}^{\phi}_{t_n}$ 和 $x_{t_{n+1}}$ 作为对比学习的正样本对。这里有一个问题： 为什么不直接使用 ground-truth 的 $x_{t_{n+1}}$ 和 $x_{t_{n}}$ 来作为正样本对，这样也不需要使用 numerical ODE solver 来求解 $\hat{x}^{\phi}_{t_n}$ 了？ 这里使用 $\hat{x}^{\phi}_{t_n}$ 的主要原因是因为它代表的是预训练好的 score-based generation model 的生成质量，而我们想要做的是 dstill 该模型的生成能力， 因此必须使用 $\hat{x}^{\phi}_{t_n}$。而在使用 Isolation 方法进行训练时，本文就直接使用 ground-truth 的 $x_{t_{n+1}}$ 和 $x_{t_{n}}$ 来作为正样本对进行对比学习。