论文题目：Transcribing Natural Languages for the Deaf via Neural Editing Programs

发表会议：Association for the Advancement of Artificial Intelligence (AAAI 2022)

第一作者：Dongxu Li (Australian National University, currently in Salesforce AI)

Question

如何通过有效挖掘 sentence 和 glossed 之间的句法联系来提高 glossification 的准确率。

Preliminary

glossification：gloss 是手语的一种书面形式，它通常是通过手语视频翻译而来，其中每个词语和手语视频中的每个动作都一一对应。 通常而言，gloss 会比 sentence (即我们日常说话使用的语句)更加简洁，同时因为它是按手语视频的动作及顺序翻译而来的，因此和 sentence 拥有不同的语法规则， 但是它拥有和 sentence 相似甚至相同的字典集(即它们所用的词汇表是相似/相同的)。 例如，对于正常的 sentence "Do you like to watch baseball games?"，表达成 gloss 就变成了 "baseball watch you like?"。 而 glossification 任务就是要将正常的 sentence 翻译为 gloss，以便后续继续翻译为手语视频。

Editing Program：对于一个给定序列 $seq_o$，可以通过一系列 editing actions 操作将其变成另一个序列 $seq_t$。 其中，editing actions 包括 1) $Add\ e\ i$，即在序列 $seq_o$ 的第 $i$ 个位置添加元素 $e$； 2) $Del\ i$，即删除序列 $seq_o$ 的第 $i$ 个位置的元素； 3) $Sub\ e\ i$，即将序列 $seq_o$ 的第 $i$ 个位置的元素替换成元素 $e$。 而将序列 $seq_o$ 变成另一个序列 $seq_t$ 的一系列 editing actions 操作称为 Eiditing Program。

Method

可以看到，glossification 是一个 Machine Tranlation 问题。最直观的做法是使用 encoder-decoder 架构，输入 sentence，输出预测的 glosses。 但是，和普通的 Machine Translation 不同的是：一方面， sentence-glosses 的数据集较少，如果直接采用传统的 Machine Translation 方式可能效果不佳；另一方面，和传统的 Machine Translation 不同， sentence 和 glosses 的字典集是相同的，仅仅是语法规则不同，这就意味着它们之间存在着很强的句法联系。因此，本文便通过利用它们之间的句法联系作为先验知识来帮助模型学习，以减轻数据集匮乏的问题。 通过观察可以看到，sentence 和 glosses 不仅字典集相同，而且在每个 sentence-glosses 对中，glosses 的大部分单词都在对应的 sentence 中出现过(通常是保留关键词，删除次要词)。 因此，相比于直接预测 glosses，可以通过对 sentence 进行增删改操作(即 editing actions)来获得对应的 glosses。 这样，通过显式地引入转化过程可以更好地帮助模型学习(即之前需要模型自己摸索如何从 sentence 转化到 glosses，现在通过一步步的 editing action 显式地告诉模型转化规则)。 所以，模型不再直接预测 glosses，而是预测 editing program，并执行它以获得最终的 glosses。 具体而言，假设 sentence 为 $x = [x_1,...,x_m]$，glosses 为 $y = [y_1,...,y_n]$，它们拥有相同的 vocabulary $V$。 模型需要预测出合理的 editing program $z = [z_1,...,z_s]$，使得 $z(x) = y$。为此，本文设计了特定的 editing program 语法，如下图所示：

其中，$ADD(w)$ 表示从字典集中选择一个 token $w$ 加入到 $y$ 的最后； $DEL(k)$ 表示删除 $x$ 中第 $k$ 个位置的 token $x_k$； $COPY(k)$ 表示将 $x$ 中第 $k$ 个位置的 token $x_k$ 复制到 $y$ 的最后； $SKIP$ 表示删除 $x$ 中余下的所有 tokens，并结束。 为了使得程序更加简洁，本文通过引入一个 $executor\ point\ k$ 来表示当前 $x$ 的编辑位置。 具体而言，初始化 $k = 1$ 表示当前 $x$ 的编辑位置在 $x_1$。 接着，每当遇到一个 $DEL(k)$ 和 $COPY(k)$ 时，$k = k+1$ 表示当前 $x$ 的编辑位置向前一步，而当遇到 $ADD(w)$ 时，$k$ 保持不变，因为 $x$ 并未被编辑。 这样一来，在模型预测 $DEL$ 和 $COPY$ 时就无需预测需要操作的位置 $k$，因为其位置都由统一的 $executor\ point\ k$ 来表示。 更进一步地，本文还引入了 $For(·)$ 来支持重复操作，例如，如果一个 editing program 的某个位置有 $3$ 个连续的 $DEL$ 操作，则可以使用 $For(·)$ 进行压缩：$DEL\ 3$ (所以面对 $DEL\ n$ 和 $COPY\ n$ 时，$k$ 需要向前 $n$ 步)。 最终，模型需要预测的内容包括：1) editing action 的 name ($ADD/DEL/COPY/SKIP$)；2) editing action 的重复次数，即 number。 (还不明白具体预测内容的可以看一下下图给出的具体例子) 这里有一个问题就是 $ADD$ 的特殊性，文章中并没有明确说明对于 $ADD$ 的预测。 我的理解是因为连续添加两个相同的词几乎不可能，因此无需预测 $ADD$ 的重复次数(默认只有一次)，而是将预测得到的 number 表示为需要添加的 token 的标号。 这样就可以将所有 editing actions 的预测统一成预测 $name + number$。

确定了模型的输入和输出形式，接下来便是输入输出数据的构造和模型的设计、训练。和普通的 glossification 不同(glossification 数据集中只有 sentence + gloss，没有 editing program)， 这里需要自己构建每个 sentence-glosses pair 对应的 editing program。为此，本文将该问题视为最短编辑距离(minimal editing distance)问题，并采用 DP 算法进行求解(剔除最短编辑距离问题中的 $Sub$ 操作)， 求得最短编辑距离，然后通过回溯确定其 editing actions 序列，则该序列就是对应的 editing program。这样便自动构造了模型的输入输出。

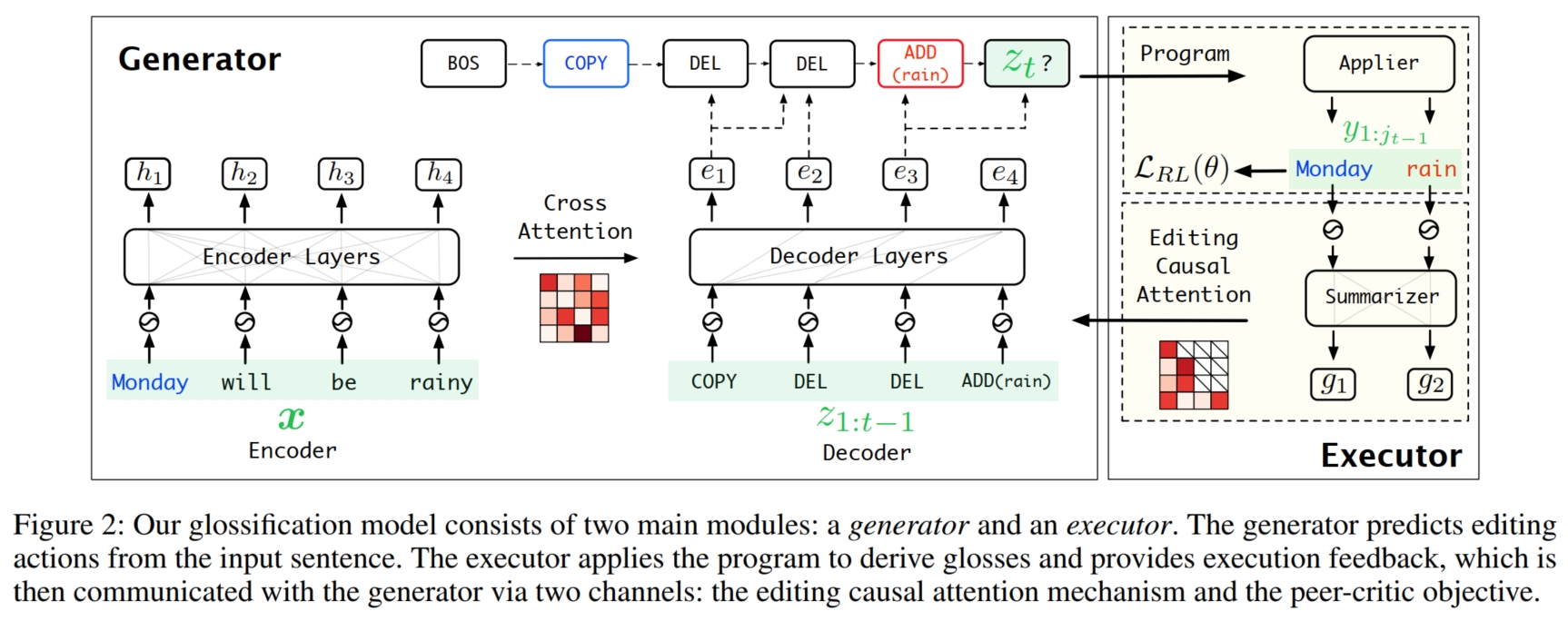
而在模型设计上，如上图，本文提出了 $generator$ 和 $executor$ 模块，前者通过深入理解 sentence 来一步步预测 editing program 中 editing action(即 step-by-step)； 后者通过执行已经预测的 partial editing program 获得 partial glosses，并将 partial glosses 进行总结归纳然后反馈给 $generator$，使 $generator$ 在下一步的预测中能关注到之前预测的情况，进一步改进自己的预测。 具体而言，对于 $executor$，给定 sentence $x$ 和 $generator$ 生成的 patial editing program $z_{1:t-1}$， $executor$ 首先在 $x$ 上执行 $z_{1:t-1}$ 获得 partial glosses $y_{1:j_{t-1}}$ (通过使用前述的 $executor\ point\ k$，注意，没有被编辑的 $x_{k+1:m}$ 不算 partial glosses 的一部分)。 然后，$executor$ 使用 Encoder 对 $y_{1:j_{t-1}}$ 进行总结：先将 $y_{1:j_{t-1}}$ 转化为 embedding $\{E_{y_1},...,E_{y_{j_{t-1}}}\}$。 然后使用 Transformer Encoder 进行编码融合获得最终的总结 hidden embedding $g_{1:j_{t-1}}$：

其中 $P_i$ 表示位置编码，$EncoderLayer(·)$ 表示 Transformer Encoder Block(包括一个 MHA(self) 和一个 FFN)，$l$ 表示第 $l$ 层。

对于 $generator$，由于仍然是一个序列预测问题，所以采用简单的 Transformer Encoder-Decoder 架构即可。 在第 $t$ 步时，其中的 Encoder 和 $executor$ 的 Encoder 类似，输入 sentence $x = [x_1,..,x_m]$，并将其映射为 hidden embedding $h = [h_1,...,h_m]$， 而 Decoder 则输入 Encoder 的输出 $h$，第 $t$ 步之前的全部预测 $z_{1:t-1}$，以及从 $executor$ 总结得到的输出 $g_{1:j_{t-1}}$， 然后预测 editing program 的第 $t$ 个 editing action $z_t$ (即建模条件分布 $P(z_t|h, g_{1:j_{t-1}}, z_{1:t-1}) \rightarrow P(z_t|x, y_{1:j_{t-1}}, z_{1:t-1})$)。 具体而言，首先将 $z_{1:t-1}$ 转化为 embedding $\{E_{z_1},...,E_{y_{t-1}}\}$，然后使用 Transformer Decoder 将 $E_{z_i}$ 和 $h_i$ 进行交互融合，得到 hidden embedding $e_{1:t-1}$：

其中 $P_i$ 表示位置编码，$DecoderLayer(·)$ 表示 Transformer Decoder Block(包括一个 masked MHA(self)，一个 MHA(cross) 和一个 FFN)，$l'$ 表示第 $l'$ 层。 注意，这里的 $DecoderLayer(·)$ 的第一个 MHA 是 masked 的。但是，因为 $y$ 的长度的动态变化性，在将 $g_{1:j_{t-1}}$ 融入到 $e_{1:t-1}$ 时不能使用常规的 Mask MHA。

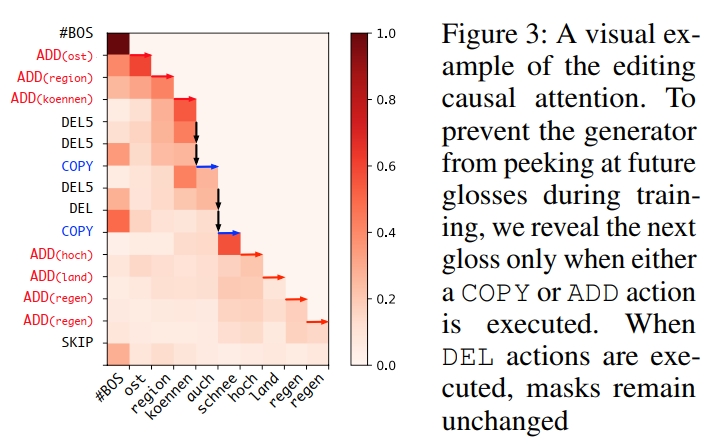
为此，本文在 Decoder 之后(即最后一层 $DecoderLayer(·)$ 之后)添加了一个 editing causal attention 模块替换 Mask MHA，并将 $executor$ 总结的 $g_{1:j_{t-1}}$ 与 $e_{1:t-1}$ 融合进行融合交互。 editing causal attention 和 Mask MHA 的结构十分类似，唯一的不同在于 Mask MHA 的 mask 是随着预测步骤 $t$ 单调递减的 (即每预测一步，就会解码出一个元素，即预测序列的长度 $+1$，mask 就 $-1$，表示该步的 ground-truth 已经可见)， 而对于 editing causal attention 而言，每预测一步只会使得 editing program 的序列长度 $+1$，并不一定会使 $y$ 的序列长度 $+1$， 只有当 editing action 是 $ADD/COPY$ 时，$y$ 的序列长度才会 $+1$，此时 mask 才能 $-1$， 而当 editing action 是 $DEL$ 时，mask 保持不变(因为此时 $y_{1:j_{t-1}}$ = $y_{1:j_{t}}$，其长度没有增加)，因此需要根据已经预测的 editing program 中的 editing action 的类型来确定每一步的 mask。 为此，本文使用 $generator\ point\ p$ 来表示当前已经预测的 $y$ 的长度，即 $j_{t-1}$。 对于预测的每一步 $t$，首先将 $p$ 初始化为 0，表示初始的 $y$ 是空的。当 $executor$ 执行一个 $ADD/COPY$ 时，$p = p + 1$ 表示 $y$ 的序列 $+1$；而当 $executor$ 执行一个 $DEL$ 时，$p$ 保持不变。 这样，就可以帮助 $generator$ 的 editing causal attention 构造 mask，其中 $> p$ 的位置全部掩码。所以 editing causal attention 的表达式如下：

其中 $Q$ 表示 $e_{1:t-1}$，$K$ 和 $V$ 表示 $g_{1:j_{t-1}}$，$M$ 表示 mask，$\bigodot$ 表示逐元素乘积，$\bigotimes$ 表示矩阵乘法。下图展示了一个 editing casual attention 的例子：

最后便是模型训练，本文首先使用了 imitation learning strategy 的策略，即将前述由 DP 算法生成的 edting program 作为唯一的 ground-truth 使用 cross-entropy 损失进行训练：

其中，$z_t^*$ 表示第 $t$ 个位置的 ground-truth，$q_t$ 表示模型第 $t$ 个位置的预测为 $z_t^*$ 的概率。 但是这会导致 program aliasing 问题，即有多个 editing program 都可以将 sentence $x$ 转化为最终的 $y$，但是却都将它们归类为错误(只有用作 ground-truth 的那个才被当作正确的)，导致模型 over-penalized， 从而导致模型的探索能力下降。为此，本文提出了使用 $policy\ gradient\ method(RL)$ 的强化学习方法来缓解这个问题(将其称为 peer-critic)。 具体而言，本文使用 $generator$ 生成的 glosses 和 ground-truth 进行计算得到的 BLEU-4 分数来作为奖励，并通过 minimize the negative expected reward 来训练模型：

其中 $\tilde{z}$ 表示模型 $P_{\theta}(z|x)$ 预测的 editing program，$r(·)$ 表示奖励函数，即 BLEU-4 分数。 由于 BLEU-4 分数的计算是不可导的，无法进行 back-propagation，本文使用了 REINFORCE 算法，使用 Monte-Carlo 采样来计算梯度：

其中，通过采样 $K = 5$ 次 $\tilde{z}$ 来计算近似的 expected rewards (即损失函数 $E[·]$)。最后，通过结合这两个损失函数，便可进行训练：