论文题目：Prompt-to-Prompt Image Editing with Cross-Attention Control

发表会议：International Conference on Learning Representations (ICLR 2023)

第一作者：Amir Hertz (Google Research)

Question

如何提高 Instruction-based image editing model 的性能(即仅仅使用 Instruction/text 来对输入的图像进行编辑， 例如：输入文字“将图像的 xx 物体去掉/在 xx 位置添加一个 xx 物体”和一张给定的图像，就可以获得按照文字要求编辑后的图像)

Method

针对图像编辑最常见的方法是使用 mask 来显式确定需要编辑的区域，然后使用不同的方法对 mask 内的区域进行编辑。 但是 mask 过程很繁琐，不如直接文本驱动的编辑。此外，对图像内容进行 mask 会消除重要的结构信息，使得在后面修复过程中完全看不到先前的信息。 因此，本文提出一种仅使用文本进行编辑的方法，通过 Prompt-to-Prompt 的操作，在预训练的 text-to-image 扩散模型中对图像进行语义编辑。 通过深入研究交叉注意力层(cross-attention)，并探索其控制生成图像的语义强度(即通过定向改变 cross-attention 能多大程度上控制图像的变化)。 本文主要考虑 U-net 内部的 cross-attention maps，这是一个高维张量，结合了从提示文本中提取的 token 和需要生成的图像的 pixel 之间的对应关系。 这些 maps 包含丰富的语义关系，对生成的图像有重要影响。 因此，本文提出一个简单直观的想法：可以通过在扩散过程中注入不同的交叉注意力图来编辑图像，以在指定的扩散步骤中，控制每个 pixel 关注提示文本的对应 token。

不同与传统的方法(给定一张原始图像和编辑指令)，本文需要给定原始图像(即需要编辑的图像)的标题 $\mathcal{P}$，以及目标图像(即编辑完成的图像)的标题 $\mathcal{P}^*$。 这就需要将编辑操作写入到 $\mathcal{P}$ 以获得 $\mathcal{P}^*$。本文关注的编辑操作(常见的)包括 $3$ 种：change (替换)，即将 $\mathcal{P}$ 中的某个词替换为另一个词； Add (添加)，即在 $\mathcal{P}$ 中添加新词(对于删除词只需要将 $\mathcal{P}$ 变成目标图像标题，$\mathcal{P}^*$ 变成原始图像标题就可以变成添加词)； Scale (缩放)，即放大/缩小 $\mathcal{P}$ 中的某个词的表现程度。 假设 $\mathcal{I}$ 表示使用现成的 text-to-image DM 模型输入 $\mathcal{P}$ (和随机种子 $s$)生成的图像。 本文的目标是仅使用编辑提示 $\mathcal{P}^*$ 的指导，编辑图像 $\mathcal{I}$，以获得编辑后的图像 $\mathcal{I}^*$，它保持了原始图像的内容和结构，仅修改对应的编辑提示要求的内容。 一种简单的方法是固定随机种子($=s$)，然后使用同样的 text-to-image DM 模型输入 $\mathcal{P}^*$ 再次生成图像作为编辑后的图像，但是这样会导致整张图像的全部变动。 这说明仅仅固定随机种子还是无法解决模型生成的随机性。为此，本文便通过固定 U-net 内部的 cross-attention maps 来进一步限制模型的输出。

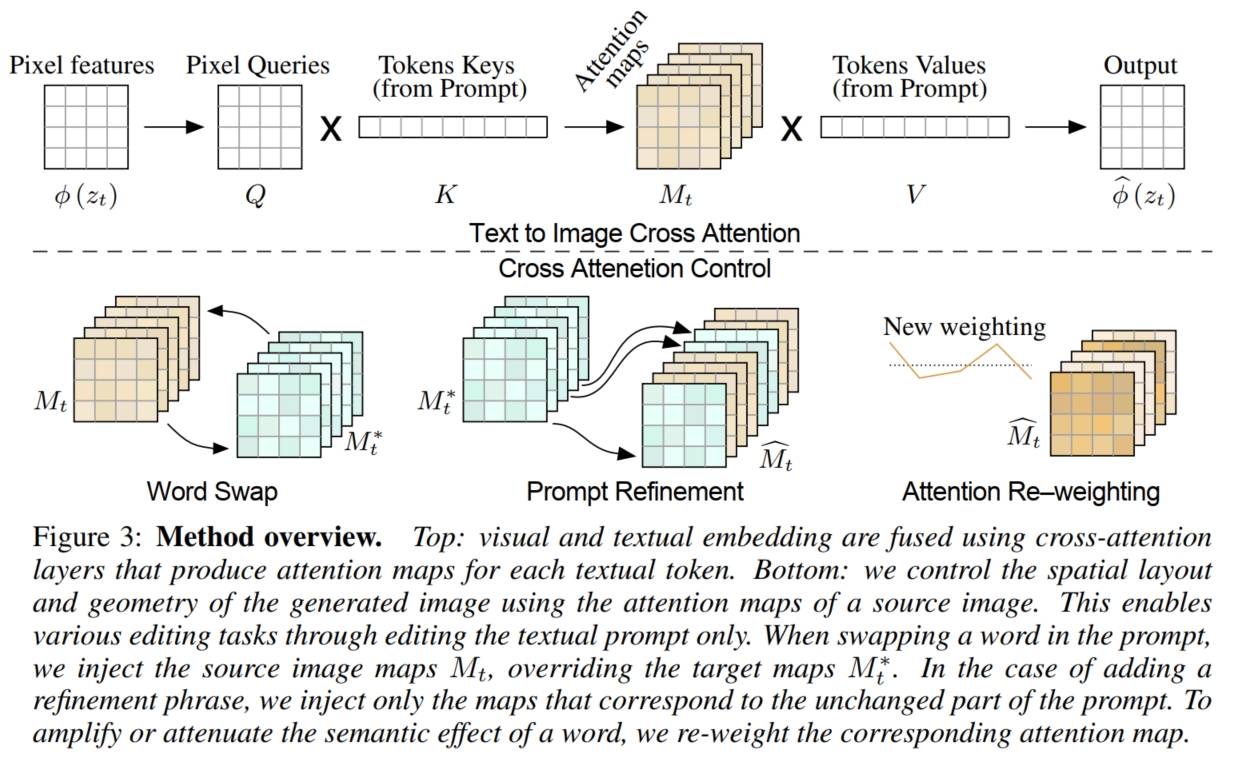
具体而言，如上图，假设输入的原始图像的标题 $\mathcal{P}$ 经过 text embedding 后转化为 embedding $\psi(\mathcal{P})$，输入的原始含噪图像为 $z_t$。 其中，$z_t$ 在经过 U-net 的 encoder 编码后进一步压缩为 embedding $\phi(z_t)$，然后 U-net 使用 cross-attention 来将 text 和 image 进行交互：

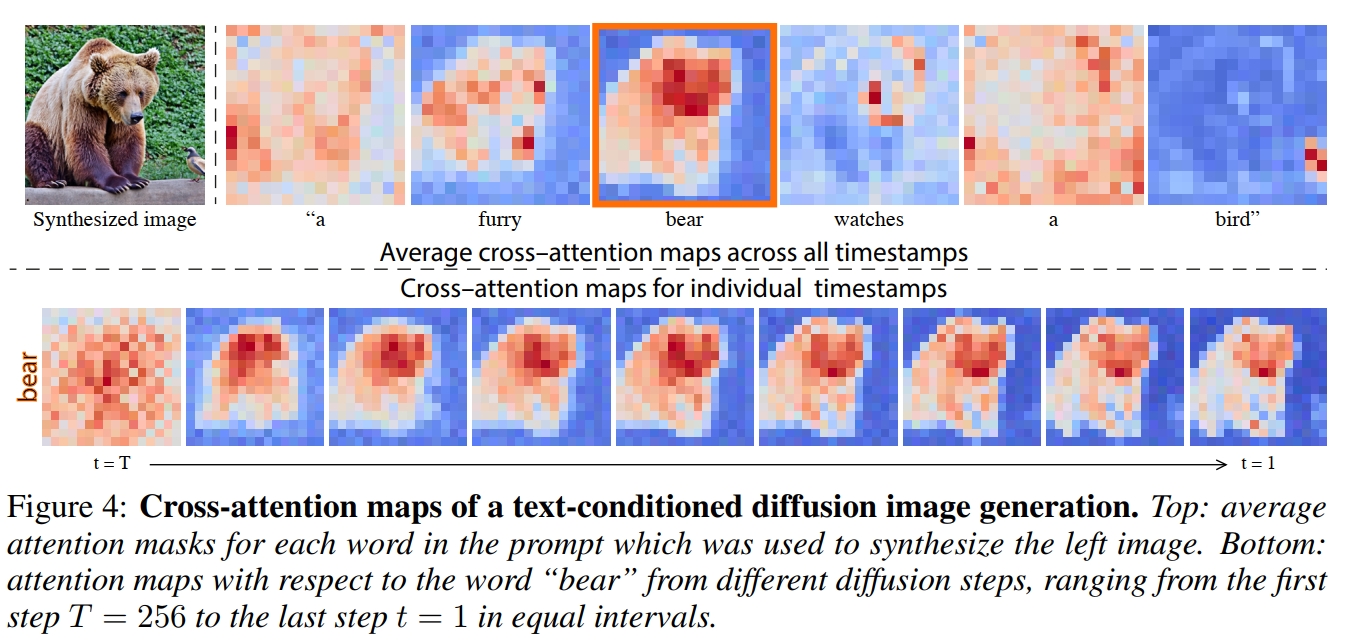
其中，$l_{Q/K/V}(·)$ 表示各自的线性投射层，$M$ 则是 cross-attention map。最终更新后的 $\hat{\phi}(z_t)) = MV$。 直观上看，交叉注意力输出 $MV$ 是值 $V$ 的加权平均值，其中权重是 attention map $M$，它与 $Q$ 和 $K$ 之间的相似性相关。 同时，通过观察，如上图(Figure 4)，本文发现生成图像的空间布局和几何形状依赖于 cross-attention map：像素更容易被描述它们的词语所吸引(即注意力分数更高)，且在扩散过程的早期阶段，图像的结构布局就已经确定好了。 因此，我们可以将通过原始提示 $\mathcal{P}$ 得到的 cross-attention map $M$ 注入到通过目标提示 $\mathcal{P}^*$ 中。 这使得编辑图像 $\mathcal{I}^*$ 的合成不仅可以根据编辑的提示 $\mathcal{P}^*$ 进行操作，而且还保留了输入图像 $\mathcal{I}$ 的结构。 具体算法流程如下图，假设 $DM(z_t/z_t^*,\mathcal{P}/\mathcal{P}^*,t,s)$ 是现成的 text-to-image DM 模型的一步生成过程，其输出更新的噪声图像 $z_{t-1}/z_{t-1}^*$ 和 U-net 生成的 cross-attention map $M_t/M_t^*$； $DM(z_t,\mathcal{P},t,s)(M \leftarrow \hat{M})$ 表示在一步生成时，将 U-net 需要的 cross-attention map 由 $M$ 更换为 $\hat{M}$； $\hat{M} = Edit(M_t,M_t^*,t)$ 表示通过将原始图像的 $M_t$ 注入到目标图像的 $M_t^*$，生成更新的 cross-attention map $\hat{M}$。 具体而言，本文对每一步的逆扩散生成过程都使用注意力注入机制。 在第 $t-1$ 步的逆扩散生成过程时，首先使用原始图像标题 $\mathcal{P}$ 和上一步生成的含噪原始图像 $z_{t}$ 生成更新后的含噪原始图像 $z_{t-1}$ 和本次生成过程使用的 cross-attention map $M_t$： $z_{t-1}, M_t \leftarrow DM(z_t,\mathcal{P},t,s)$。 然后使用目标图像标题 $\mathcal{P}^*$ 和上一步生成的含噪目标图像 $z_{t}^*$ 生成本次生成过程使用的 cross-attention map $M_t^*$。 接着使用 $Edit(·)$ 的注入机制将 $M_t$ 注入到 $M_t^*$ 中获得更新的(目标图像生成使用的) cross-attention map $\hat{M}_t \leftarrow Edit(M_t,M_t^*,t)$。 最后使用更新的 $\hat{M}_t$，目标图像标题 $\mathcal{P}^*$ 和上一步生成的含噪目标图像 $z_{t}^*$ 生成更新后的含噪目标图像 $z_{t-1}^*$。 最终通过 $T$ 步逆扩散生成过程，便可同时生成原始图像 $z_0$ 和编辑完成的图像 $z_0^*$。

回顾上述算法，我们将原始图像的 $M_t$ 注入到目标图像的 $M_t^*$ 中的主要目的是为了让目标图像仅在 $\mathcal{P}^*$ 要求编辑的位置上进行编辑，而其他位置保持和原始图像一致。 因此，我们在注入时可以使用一个简单的方法，即对于 $\mathcal{P}^*$ 要求编辑的位置(像素位置 $(i,j)$)，我们使用目标图像的 $M_t^*(i,j)$，而对于其他位置，我们使用原始图像的 $M_t(i,j)$。 具体而言，对于 Word Swap (即 change) 任务，因为是替换一个/几个词，其句子的长度没有变化，所以 cross-attention map $M$ 的形状也没有变化，可以直接使用 $M_t$ 将 $M_t^*$ 替换掉 (如果是使用一个词替换几个词或者几个词替换一个词，句子长度发生变化，本文使用将 $M$ 的对应位置进行复制/取平均来使得句子长度保持不变)。 但是这样就和生成原始图像没有区别，没有将替换的词的关系体现出来，结合上述提到的 DM 模型生成过程通常在早期阶段就将图像的结构布局生成完成， 因此，我们可以在 DM 模型生成的早期 ($\tau < t < T$)，使用 $M_t$ 将 $M_t^*$ 替换掉来生成整体布局；而在后期，则使用正常的 $M_t^*$ 来使得模型关注被替换的词，从而实现编辑位置的改变。 因此，$Edit(·)$ 的公式为：

对于 Prompt Refinement (即 Add) 任务，因为是添加词，句子长度发生变化，因此本文仅对 $\mathcal{P}$ 和 $\mathcal{P}^*$ 中相同的词进行注意力注入， 而对于 $\mathcal{P}^*$ 中新增的词则使用正常学习。同时和 Word Swap 一样，也只在早期使用注意力注入。因此，$Edit(·)$ 的公式为：

其中，$A(j)$ 表示 $\mathcal{P}^*$ 中的第 $j$ 个词对应 $\mathcal{P}$ 中的第 $A(j)$ 个词。 对于 Attention Re–weighting (即 Scale)任务，因为没有词的变化，只有对于词的表现程度的变化， 因此只需要将整个 $M_t^*$ 替换为 $M_t$，并改变 $M_t$ 中的指定词的权重即可(需要对词的表现程度进行放大就增大对应词的权重，反之则减小权重)。 具体的 $Edit(·)$ 的公式为：

其中 $j^*$ 表示指定的词的位置，$c \in [-2, 2]$。但是，对于局部编辑来说(例如只是将图像中的某个物体更换为另一个物体)， 我们需要更强的约束条件来限制模型的输出。因此，对于 Local Editing，我们可以先确定需要编辑的物体，然后构造一个 mask，使得模型只能在 mask 指定的区域进行编辑，而保持其他位置不变。 通过这种强制的“freeze”未编辑的区域，能更好地保持区域不变性。 具体而言，在前述中可以看到，物体的 cross-attention map $M$ 已经和最终其所在的图像的位置很接近。 因此，假设需要编辑的物体在 $\mathcal{P}^*$ 中为 $\omega$，则在第 t 步的生成过程中，本文使用 $T \sim t$ 步对应的 $\omega$ 所生成的 cross-attention map 的平均值 作为 average cross-attention map $\bar{M}_{t,\omega} = \dfrac{\sum_{i=T}^t M_{i,\omega}}{T - t}; \bar{M}^*_{t,\omega} = \dfrac{\sum_{i=T}^t M_{i,\omega}^*}{T - t}$。 然后使用二值函数创建 mask $\alpha = B(\bar{M}_{t,\omega}) \cup B(\bar{M}^*_{t,\omega})$，其中 $B(x) := x > k, k=0.3$。 为了支持编辑物体的几何修改，编辑区域应该同时包含原始和新编辑物体的轮廓，因此，本文使用的最终的 mask 是二值函数的并集 $\alpha$。 最后使用 mask $\alpha$ 对图像进行掩码即可获得更新的图像：