论文题目：Improving Sign Language Translation with Monolingual Data by Sign Back-Translation

发表会议：Conference on Computer Vision and Pattern Recognition (CVPR 2021)

第一作者：Hao Zhou (USTC, Baidu VIS now)

Question

如何解决 Sign Language Translation (SLT) 的数据缺乏问题

Method

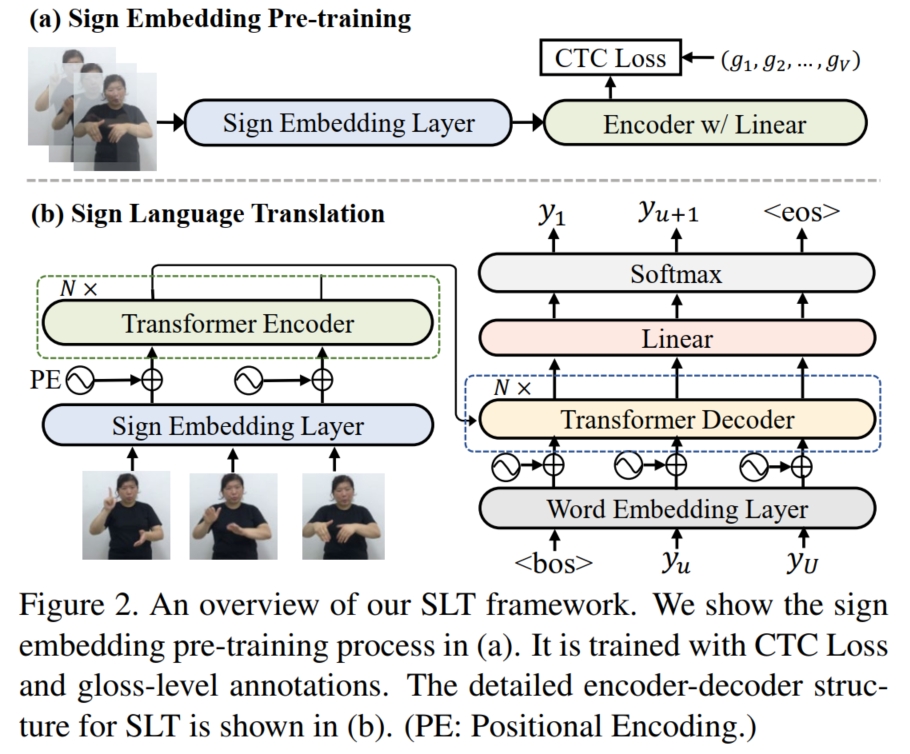
本文提出了使用 sign back-translation (SignBT) 的方式生成伪数据来解决数据缺乏问题。 假设原始数据集为 $D_{origin}^{(1:M)}$，输入手语视频为 $\mathbf{x} = \{x_t\}_{t=1}^T$，输出 sentence 为 $\mathbf{y} = \{y_u\}_{u=1}^U$， 而对应的 $glosses$ 为 $\mathbf{g} = \{g_v\}_{v=1}^V$。由于现实中拥有非常多的 sentence data，也叫 monolingual data。 本文便打算使用 back-translation 将 sentence 翻译为伪手语视频 $\hat{\mathbf{x}}$。 最直接的方法是先用现有的数据集 $D_{origin}^{(1:M)}$ 训练一个 text-to-sign 模型(输入 sentence，输出 sign video)， 然后使用额外收集的 sentence 集合 $\hat{\mathbf{y}}^j, j = [1,...,N]$ 输入到训练好的 text-to-sign 模型中，输出预测的手语视频 $\hat{\mathbf{x}}^j$。 这样生成的 $\{\hat{\mathbf{x}}^j,\hat{\mathbf{y}}^j\}$ 便可以作为伪数据集加入到原始数据集 $D_{origin}^{(1:M)}$ 一起训练一个 SLT 模型。 但是由于 sentence 和 video 的 modal gap，导致使用原始的小数据集训练出来的 text-to-sign 模型效果不好，继而影响生成的伪数据 $\hat{\mathbf{x}}^j$ 的质量。 因此，本文采用了两阶段的 back-translation 方法，在 text-to-gloss 阶段，由于 sentence 和 $glosses$ 的 modal 相似性， 本文直接训练了一个 text-to-gloss 的模型来将 sentence 翻译为 $glosses$； 而在 gloss-to-sign 阶段，由于仍然存在 $glosses$ 和 video 的 modal gap， 本文便放弃了使用模型直接生成的方式，而是充分采用了 $gloss$ 和 sign video 的单调性，使用分割的方式获得伪 video。 最终生成伪数据集 $\{\hat{\mathbf{x}}^j,\hat{\mathbf{y}}^j\}$。

具体而言，如上图 (Figure 2)，在 text-to-gloss 阶段， 本文首先使用原始数据集 $D_{origin}^{(1:M)}$ 的 $\{\mathbf{y}^i, \mathbf{g}^i\}, i = [1,...,M]$ 训练了一个 text-to-gloss 的模型 $\boldsymbol{M}_{BT}(·)$。 然后使用大量和原始数据集 $D_{origin}$ 的 $\mathbf{y}^i$ 相同 domain 的其他 sentence(monolingual data，例如维基百科上的句子等) $\hat{\mathbf{y}}^j, j = [1,...,N]$ 输入训练好的模型 $\boldsymbol{M}_{BT}(·)$ 中， 并输出预测的 $glosses\ \hat{\mathbf{g}}^j$，则生成的 $\{\hat{\mathbf{y}}^j, \hat{\mathbf{g}}^j\}$ 对就可以作为 gloss-to-text 的伪数据集。

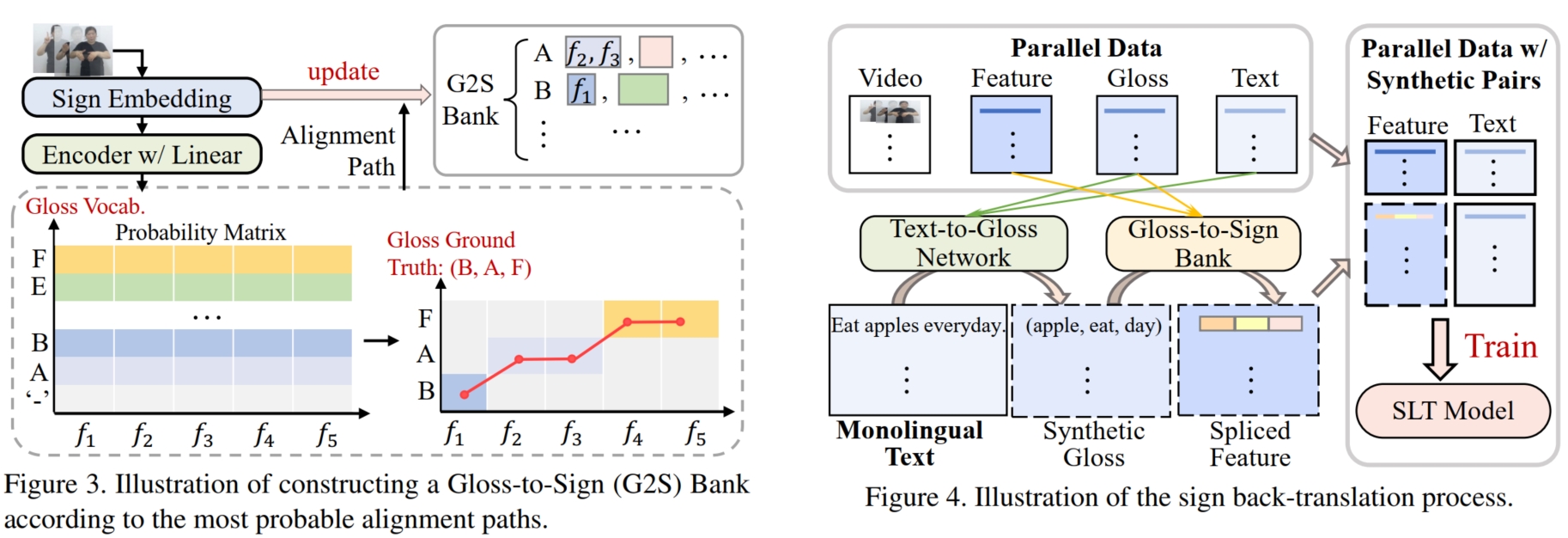
而在 gloss-to-sign 阶段，由于 $glosses$ 和 video 的 modal gap 仍然存在，因此不能直接训练模型生成伪数据。 但是，相比于 text-to-sign，$glosses$ 的好处是它和 sign video 具有单调性，即手语视频中的每个动作都对应一个 $gloss$，且在时间顺序上和 $glosses$ 的序列顺序一致， 数学上表示为：假设 $x_{t_1:t_2}$ 对应 $g_i$，$x_{t_3:t_4}$ 对应 $g_j$，若 $i < j$，则 $t_1 < t_2 < t_3 < t_4$。 若是能够确定每个 $gloss\ g_i$ 所对应的 sign video 片段 $x_{t_l:t_r}$，则可以建立一个 gloss-to-sign 的对应表，将每个 $gloss_i$ 对应的 sign video 片段 $c_i$ 都存储起来。 那么对于 text-to-gloss 阶段生成的每一个 $\hat{\mathbf{g}}^j$，就可以按顺序将每一个 $\hat{g}_i^j$ 替换为表中相对应的 sign video 片段 $c_{i}^j$，这样就可以生成伪 sign video $\hat{\mathbf{v}}^j$。 因此，对于原始数据集 $D_{origin}^{(1:M)}$ 的 $\mathbf{v}^i$， 本文首先将其分割为 $N$ 个长度为 $\mathcal{w}$ 的相互重叠的小片段 $\mathbf{c} = \{c_n\}_{n=1}^N$ (stride $= s$，则 $N = \lceil \dfrac{T}{s} \rceil$)， 然后使用 Sign Embedding Layer $\Omega_\theta(·)$ (已经预训练好的视频编码模型)将其编码为 embeddings $\mathbf{f} = \{f_n\}_{n=1}^N$：

接着，使用 CTC classifier 来获得每个 $f_n$ 对应的 $gloss$：如下图(Figure 3)，首先将 embeddings $\mathbf{f}$ 输入到 transformer encoder 进行进一步编码， 然后使用线性层和 softmax 函数获得每个 $f_n$ 所属的 $gloss$ 的概率 $p(g_n|\mathbf{f})$，这样便可以根据每条可行路径的概率之和来计算总体概率 $p(\mathbf{g}|\mathbf{x})$：

其中，$\pi$ 表示 sign-to-gloss 的一条可行的对齐路径(如上图 Figure 3 右下角)，$\mathcal{B}$ 表示所有可行路径集。 最终将总体概率转化为 CTC loss：$L_{ctc} = -ln\ p(\mathbf{g}|\mathbf{x})$ 进行训练。

在训练完 CTC classifier 后，对于通过 $\Omega_\theta$ 得到的 $\mathbf{f} = \{f_n\}_{n=1}^N$ 和 $\mathbf{g} = \{g_v\}_{v=1}^V$， 便可以通过将 $\mathbf{f}$ 输入 transformer encoder 和 CTC classifier 获得概率 $p(g_n|\mathbf{f})$。 然后使用 Viterbi 算法在所有合法路径集 $\hat{\mathcal{B}}^{-1}(\mathbf{g})$ 中计算出一条最佳的路径：

通过最佳路径的对应关系便可获得每个 $g_i^j$ 对应的 $f_{l_i:r_i}^j$。 最后将原始数据集 $D_{origin}^{(1:M)}$ 的所有 $\mathbf{g}^i = \{g_1^i,...,g_{V_i}^i\}$ 中的每一个 $g_j^i$ 和对应的 $f_{l_j:r_j}^i$ 组成一张表， 称为 Sign Bank(由于有的 $g_i^j$ 在多个 $\mathbf{g}^j$ 中出现，所以 $g_i^j$ 和 $f_{l_i:r_i}^j$ 在 Sign Bank 中是一对多关系)。

总结而言，首先使用原数据集 $D_{origin}^{(1:M)}$ 训练一个 CTC classifier 和一个 text-to-gloss 模型。 然后根据 CTC classifier 对原数据集的所有 $gloss$ 元素 $g$ 分割出对应的 sign video clip embedding $f$，组成 Sign Bank 表。 接着使用大量额外的 sentence $\hat{\mathbf{y}}^j$，将其输入到 text-to-gloss 模型获得预测的 $glosses\ \hat{\mathbf{g}}^j$， 并根据 $\hat{\mathbf{g}}^j$ 中的每个 $\hat{g}_i^j$ 在 Sign Bank 表中选择对应的 sign video clip embedding $\hat{f}_i^j$ 进行 concat (如果有多个对应的 $f_i^j$ 就随机选择一个)， 就获得了 $\hat{\mathbf{g}}^j$ 对应的 sign video embedding $\hat{\mathbf{f}}^j$。 这样便生成了伪数据集 $D_{synth} = \{\hat{\mathbf{f}}^j,\hat{\mathbf{y}}^j\}_{j=1}^N$。

而在训练 SLT 模型时，本文使用 Transformer Encoder-Decoder 模型， 将原始数据集 $D_{origin}^{(1:M)} = \{\mathbf{x}^i, \mathbf{y}^i\}^{(1:M)}$ 中的手语视频 $\mathbf{x}^i$ 输入到 Sign Embedding Layer $\Omega_\theta(·)$ 生成 sign video embedding $\mathbf{f}^i$，并和对应的 $\mathbf{y}^i$ 组成预处理后的数据集 $\bar{D}_{origin}^{(1:M)} = \{\mathbf{f}^i, \mathbf{y}^i\}^{(1:M)}$， 然后与伪数据集 $D_{synth} = \{\hat{\mathbf{f}}^j,\hat{\mathbf{y}}^j\}_{j=1}^N$ 组成一个更大的数据集 $D_{new}$。 最后 SLT 模型便使用该数据集进行训练，输入 $\mathbf{f}$，输出 $\mathbf{y}$，使用 cross-entropy 损失：