论文题目：Attention is All you Need

发表会议：Neural Information Processing Systems (NLPS 2017)

第一作者：Ashish Vaswani (Startup)

Question

如何解决 NLP 任务无法并行训练 sequence 的问题

Preliminary

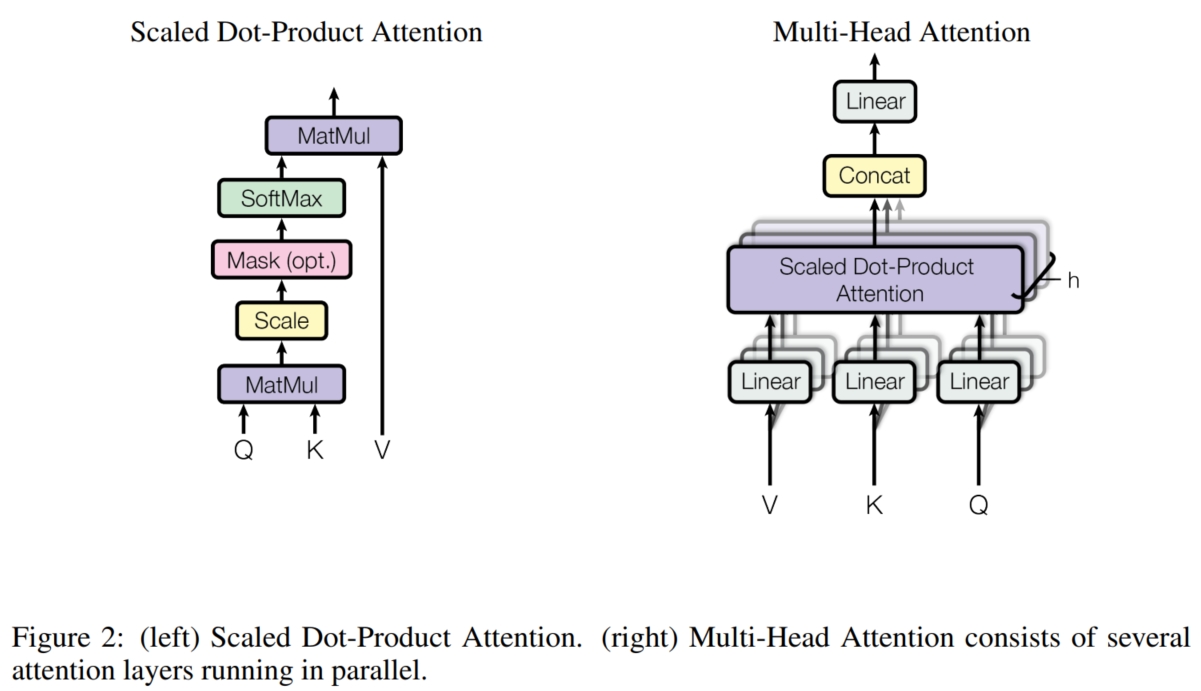
attention：attention 是将人类的注意力机制引入神经网络的一种方式。人类在进行分类等任务时，更多的是使用比较的方法来进行学习， 即对于自己的需求(即自己掌握的关键特征) $query$，通过将其与每个候选结果 $vector_i$ 的关键特征 $key_i$ 进行比较。 一般而言，两个相似的物体的关键特征也是相似的，即 $query \approx key_{positive}$。这样我们就可以选择到最终的结果。 在数学形式上，如上图(Figure 2 left)，假设当前的 $query = q$，各个候选的结果 $\{vector_i, key_i\},\ i = [1,...,N]$ 为 $\{k_i, v_i\}$， 则首先我们可以计算 $q$ 和 $k_i$ 之间的相似度来确定其与各个候选结果的相似性(最简单的使用点乘表示相似度)：

然后，我们可以根据每个候选结果的相似性来选择，相似性越高的选的越多，反之选的越少(Rule1)：

但是这样会产生一个问题，即 $result$ 的数量级 $\approx$ $q$ 的数量级 $+$ $k$ 的数量级 $+$ $v$ 的数量级， 会远远大于候选结果 $v$ 的数量级。因此我们要将相似度进行缩放，将其表示为每个候选结果在 $result$ 中的占比， 这样既保持了 Rule1，又使得 $result$ 和 $v$ 的数量级保持一致。为此，可以使用 $softmax(·)$ 将相似度转化为占比：

最终，$result$ 的表达式为：

Method

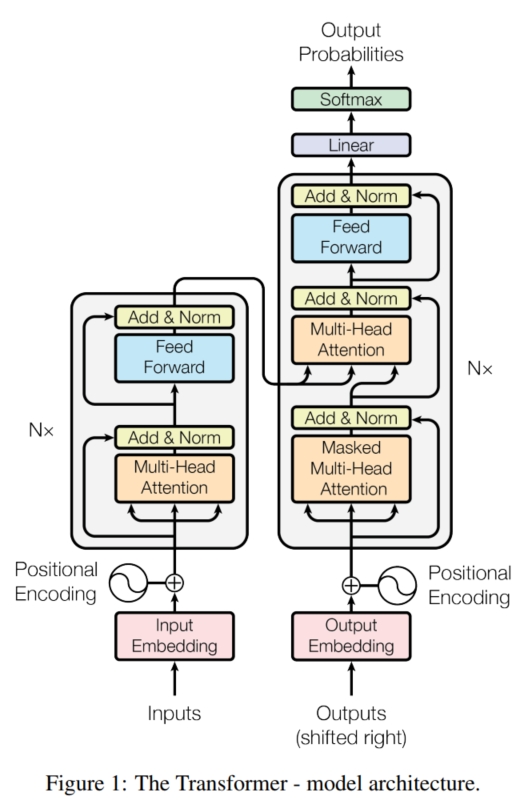
传统的 recurrent 模型在序列建模的准确率上已经有了很大的改进，但是其最致命的问题是其训练的顺序性， 导致其训练与推理时长和训练样本的长度成正比，这极大限制了模型可处理的序列长度；而且，只要 recurrent 模型的架构不变(CNN + 隐变量 $h_i$)，这个问题基本上无法解决。 为此，本文放弃了 recurrent 模型的架构，采用了全新的基于 attention 的架构 $Transformer$。 它保留了 Encoder-Decoder 的框架，但是实现了 Encoder 编码序列的并行。 具体而言，如上图，假设输入序列为 $x = (x_1,...,x_n)$，需要将其转化为 $y = (y_1,...,y_m)$。 对于 Encoder，它需要将输入序列 $x$ 转化为中间表示 $z = (z_1,...,z_n)$。它是由一个个 Encoder Block 组成，每个 Encoder Block 的结构相同。 每个 Encoder Block 的主要作用是学习输入序列之间的相互关系，因此需要 attention 来不断关注序列中其他元素与自身的关系。 它主要由 Multi-Head Attention (MHA)、Feed Forward Network 和 LayerNorm 组成。 对于输入序列的每一个元素 $x_i$，首先将其映射到 $d_q, d_k, d_v$ 维度，分别表示为 $q, k, v$：

然后使用 attention 关注自身与序列中的其他元素的关系来更新自身的表示：

容易看出，上述的操作可以将 $x$ 视为一个矩阵，使得各个元素可以同时进行计算，即：

由于 $QK^T$ 的数量级 $\approx d_q \times d_k \approx d_k^2$，为防止计算数值过大，本文选择将乘积结果 $\times \frac{1}{\sqrt{d_k}}$ 进行缩放， 因此，attention 的表达式为：

更进一步地，在 CNN 架构中，模型通过卷积核来关注每个元素自身与其他元素的关系，并通过多个不同参数的卷积核来鼓励模型学习多种不同的关系。 同样地，这里可以选择通过多个不同 $W_q, W_k, W_v$ 参数的 attention 来鼓励模型学习不同的关系。具体而言，本文提出了 Multi-Head Attention 机制。 如上图(Figure 2 right)，它使用 $h$ 组参数 $W_q^i, W_k^i, W_v^i$ 将输入投射到不同的表示(每组维度仍然是 $d_q, d_k, d_v$)，然后对每组实行 attention 来学习一种关系，以鼓励模型从不同的角度关注输入的不同子空间：

这样每个 $\hat{x}^i$ 都表示 $x$ 的一种子空间表示，最后将其 concat 起来，并经过进一步线性投影使得输出的维度保持不变：

然后，通过借鉴 ResNet 的做法，使用残差连接进行残差建模学习：$\hat{x} = \hat{x} + x$。 同时由于 NLP 的每个 batch 中的数据的长度不一致，无法较好地使用 $BatchNorm(·)$ 进行学习，本文便采用 $LayerNorm(·)$ 对输出进行归一化：

在经过了 MHA 的序列元素间的相互学习之后，模型还需要对每个元素自身进行进一步总结学习。为此，本文在 MHA 之后添加了一个 $2$ 层全连接网络(FFN)对每个元素进行独立地学习：

其中，激活函数使用简单的 ReLU。同时，也在其后添加了同样的残差连接和层归一化。最后，通过不断堆叠 MHA + FFN (为一个 Encoder Block)来学习输入，获得中间表示 $z$。

而对于 Decoder，它需要将中间表示 $z$ 转化为最终输出 $y$。它也是由一个个 Decoder Block 组成， 每个 Decoder Block 的主要作用是学习输入序列和输出序列之间的相互关系，因此需要 attention 来不断关注两个序列之间的关系。 和 Encoder Block 类似，它主要由 Masked Multi-Head Attention、 Cross Multi-Head Attention、Feed Forward Network 和 LayerNorm 组成。 其中 Cross MHA 和 MHA 的架构一致，只是其 $K$ 和 $V$ 为 Encoder 的输出 $z$，而 $Q$ 为前一层 Decoder Block 的输出(第一层的 Decoder Block 的 $Q$ 为之前的预测输出 $\hat{y}_{1:t}$)。 而对于 Masked MHA，由于 Decoder 的解码是顺序性的，即一次解码一个序列元素，然后将预测的输出加入到 Decoder 的输入中($\hat{y}_{1:t}$ 表示已经预测了 $t$ 个)进行进一步预测下一个序列元素 $\hat{y}_{t+1}$； 而 MHA 机制是全局性的，即任意一个元素都能关注到其他所有元素，使得模型会”偷窥“到当前和之后还未预测的输出 $y_{t+1:m}$。为了避免这个问题，本文使用 Masked MHA 将 $t+1 \sim m$ 之间的元素全部掩码，使得模型无法看到。 具体而言， Masked MHA 的整体结构和 MHA 相似，它在计算 softmax(·) 时，将所有 $t+1 \sim m$ 位置的输入都变成 $-\infty$，这 样在经过 softmax(·) 之后，其对应位置得到的占比就变成 $0$，就保证了模型不会关注 $t+1 \sim m$ 位置的元素(原文的说法是阻止向左的信息流并保持其自回归特性)。

最后，对 Decoder 的输出进行线性投影 $L_o$ 来改变维度(变成 vocabulary size)，并使用 softmax 来获得预测的每个元素的概率。 同时，在 Encoder 和 Decoder 输入时，将 $x_i$ 和 $y_i$ 进行线性投影 $L_i^e$ 和 $L_i^d$ 转化为可学习的 embeddings 以便更好地学习(本文对 $L_o/L_i^e/L_i^d$ 使用同一个矩阵)。

由于 attention 对元素之间的距离是 un-aware 的，这就导致打乱输入和输出序列的顺序对模型没有影响，即会导致模型预测的输出没有顺序性。 因此，需要给模型添加位置信息，本文使用构造 "position encodings" 并加入到 Encoder 和 Decoder 开始的输入中来使得模型感知位置信息。 具体而言，本文采用不同频率的正余弦函数来表示位置信息，即 "position encodings"：

其中，$pos$ 表示序列的第 $pos$ 个元素($pos = [1,...,n\ or\ m]$)，$i$ 表示序列元素的第 $i$ 个维度($i = [1,...,d_{model}]$)。 当然，也可以和 Encoder/Decoder 的序列输入一样，直接把每个元素的位置信息都变成一个可学习的 embedding 让模型自己学习。 但是这种方法当在推理时遇到比在训练时遇到的最长序列还长时，就为超出的序列增加位置信息，而正余弦函数可以进行扩展。 此外，正余弦函数符合相对关系不变(即平移不变性)，即 $PE_{pos+k} \infty PE_{pos}, \forall fixed\ k$。

总结而言，Transformer 通过将 $x$ 转化为 learned embedding，加上 "position encodings" 作为输入进入 Encoder，输出中间表示 $z$。 接着将已经预测好的输出 $\hat{y}_{1:t}$ 转化为 learned embedding，加上 "position encodings" 作为输入和 $z$ 一起进入 Decoder. 最终输出的第 $t$ 个位置的元素经过线性投影 $L_o$，并使用 softmax 来获得第 $t$ 个位置的元素预测概率，最后使用 cross-entropy 损失进行训练。