这篇博客主要介绍了 PyTorch 的 autograd 机制及其具体实现方式。

从手推公式到自动化

训练一个模型的范式是构造模型 $\mathcal{M}$ 和数据 $\mathcal{D} = \{x_i,y_i\}_{1:N}$，使用模型的前向过程计算 loss：l = M.forward(xi,yi)，然后使用l.backward()计算 gradient，最后使用optim.step()更新模型参数。

那么 PyTorch 是如何计算每个参数的梯度的，即 PyTorch 的自动求导机制(torch.autograd)？首先让我们回顾一下如何手推一个具体表达式关于其每个输入的偏导数（即梯度）的：假设输入为 $x$ 和 $y$，将 $x^2$ 和 $y$ 的和乘以 $2$ 得到结果 $z$：$z = 2 * (x^2 + y)$；则可以通过先对 $(x^2 + y)$ 求关于 $z$ 的导数得到 $\frac{\partial z}{\partial (x^2 + y)} = 2$；然后再求 $x^2 / y$ 关于 $(x^2 + y)$ 的导数得到 $\frac{\partial (x^2 + y)}{\partial x^2} = 1; \frac{\partial (x^2 + y)}{\partial y} = 1$；接着，再求 $x$ 关于 $x^2$ 的导数得到 $\frac{\partial x^2}{\partial x} = 2x$；最后，将各个部分进行相乘即可得到 $x / y$ 关于 $z$ 的导数：

这就是我们熟知的链式法则求导，但是如何将其自动化呢？通过观察我们可以看到：第一，在链式法则每次求导的过程中（$\frac{\partial z}{\partial (x + y)}\ \text{or}\ \frac{\partial (x + y)}{\partial x}$），都是使用初等函数的求导法则；也就是说，不论给定的表达式有多复杂，我们都可以将其分解为多个初等函数的“顺序”执行。这样，我们就可以将所有的初等函数都实现为各自的初等函数类，其中每个初等函数类都提前实现各自的导数计算过程。

第二，在链式法则求导的过程中，如果每一步都直接对导数进行累乘（例如在计算完 $x^2$ 关于 $(x^2 + y)$ 的导数后，直接将 $(x^2 + y)$ 关于 $z$ 的导数累乘到其上，$\frac{\partial (x^2 + y)}{\partial x^2} = 1 = \frac{\partial z}{\partial (x^2 + y)} = 2 * \frac{\partial (x^2 + y)}{\partial x^2} = 1$）,则每个当前初等函数的导数计算只与自身的输入和前一个初等函数的导数有关（例如 $\frac{\partial x^2}{\partial x}$ 只与自身的输入 $x$ 和 $\frac{\partial (x^2 + y)}{\partial x^2}$ 有关），而与更之前（如 $\frac{\partial z}{\partial (x^2 + y)}$）或之后的初等函数的导数无关。因此，对于每一个初等函数类，我们都可以将其的求导函数进行规范化：输入上一个执行的初等函数计算得到的导数 $g_{p}$ 和当前初等函数自身的输入 $i$，先计算得到当前初等函数的导数 $g_c$，最后将其与 $g_p$ 进行累乘得到最终的导数 $g_o$，作为下一个初等函数的输入。这样，每个初等函数的输入输出就规范化为 [$1$ 个导数，已知数量的输入数据] $\rightarrow$ [已知数量的导数]；而不需要由于不同的表达式的链式法则的长度而接受不同长度的导数输入，极大方便了初等函数类的编写。下图为指数函数类的求导函数的简单实现：

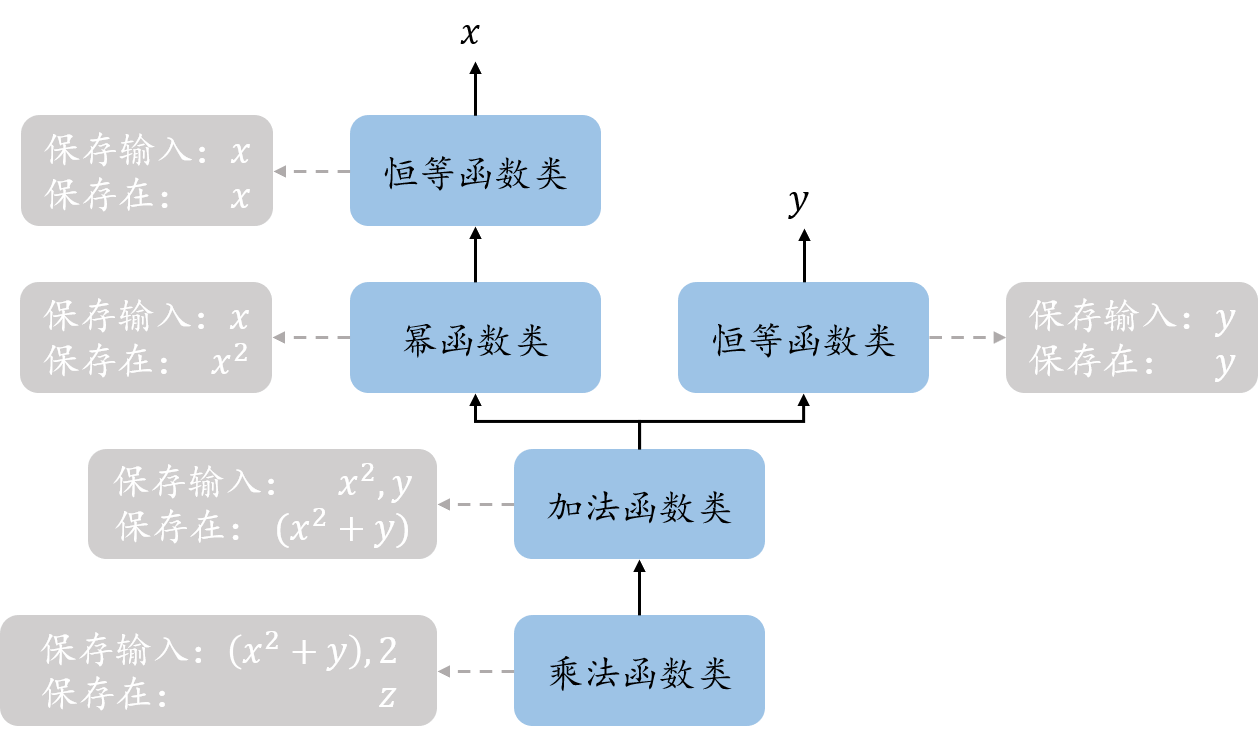
现在，我们已经将任意表达式的求导分解为有限的初等函数的“顺序“执行”，同时也完成了每个初等函数的具体求导函数的实现。但是如何实现求导顺序确定和导数传递的自动化，即为什么先求解 $(x^2 + y)$ 关于 $z$ 的导数，以及 $(x^2 + y)$ 关于 $z$ 的导数如何传递给 $(x^2 + y)$。Torch 的做法是在表达式计算的过程中（即前向过程）构建一个和链式法则顺序性一致的有向无环图（称为计算图），其中方向表示链式法则的计算方向，每个节点表示对应的初等函数类，并将每个节点保存在各自的输出数据中（例如最开始的乘法函数节点保存在 $z$ 中）。同时，在表达式计算的过程中（即前向过程）将每个节点的输入数据保存在节点中（例如 $2$ 和 $(x^2 + y)$ 保存在最开始的乘法函数节点中），这样，在需要计算导数时，可以从表达式的结果数据中取出节点（即是最开始的节点），给它输入一个起始的导数，其就可以根据 [起始的导数，自身保存的输入数据] 求解得到自身的导数；然后根据计算图找到下一个求导的节点，并将计算得到的导数传递给它作为输入。这样便可实现真正的自动求导机制（我们只需在最开始给一个起始导数，便能得到每个输入数据的导数）。下图为表达式 $z = 2 * (x^2 + y)$ 的计算图：

Torch Autograd

现在只剩一个问题了，就是如何构建计算图？在讲解如何构造计算图之前，我们先将上述介绍的自动求导流程使用 torch 的专有名词再描述一遍，以便将 Torch 中的各个专有名词和上述介绍的自动求导流程中的各个元素对应起来。通俗而言，torch.autograd在模型 forward（即表达式计算）的同时构造了一个 DAG 的 computational graph（即计算图），计算图中的每个节点由 Function 类（即初等函数类）的实例组成；其中的叶子节点表示需要计算梯度的输入数据和模型参数 (即.required_grad=Ture的数据，即 $x$ 和 $y$)，而非叶子节点表示模型对这些输入数据和参数进行的初等函数运算(加法，乘法等，elementary operations)。然后在 backward（即从表达式的结果数据中取出节点，给它的differentiate()输入一个起始的导数）的时候触发每个节点的 gradient 计算（即后续每个节点的differentiate()的自动计算），并将计算完成的 gradient（即导数）存储在各自对应的输入数据（即每个节点保存的输入数据）的.grad属性内。最后 optimizer 的 step 执行时将每个参数的值使用对应.grad属性内的 gradient 进行更新计算：p = p - lr * p.grad。

更具体而言，首先，torch 构造的计算图是一个有向无环图(DAG)。其中，叶子节点为输入的 tensor，包括需要计算梯度的输入的数据和参与计算的模型参数（两者都只有当.required_grad=Ture时才会出现在计算图中），根节点为最终输出的 tensor，而中间节点是模型执行的每个初等函数运算(简称为执行操作)。假设a和b是torch.Tensor变量，且M = lambda x, y: 3*x**3 - y**2，则在out=M(a,b)时，torch.autograd构造了如下的 DAG，其中每一个节点表示一个初等函数：

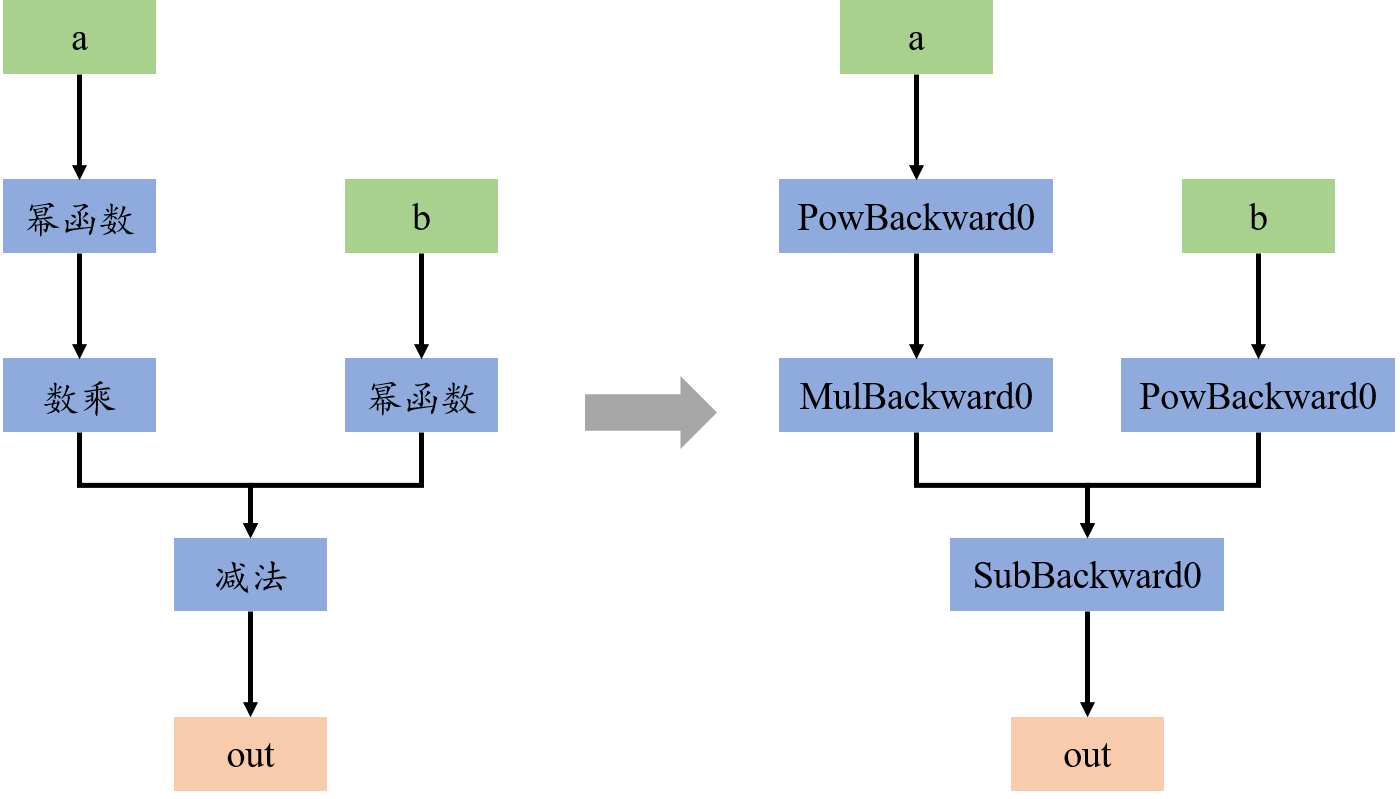
其中，蓝色节点表示执行操作节点，在torch.autograd中使用Function类来实现。每个初等函数都实现了一个Function子类，例如幂函数为PowBackward0类。在Function类中，需要实现forward和backward函数，其中前者在模型前向运算时使用，而后者在后向梯度运算时使用。而且每个执行操作Function实例都保存在其输出 tensor 的.grad_fn属性上。以下为指数函数的Function类简易实现：

接下来便是如何构建计算图，主要包括两个部分：构建节点和构建节点之间的连接关系。对于第一个部分，Torch 的实现方式为在每执行一个初等函数操作后立即生成一个对应的执行操作节点 $N_i$，并将该执行操作节点 $N_i$ 保存在其输出 tensor 的.grad_fn属性上；同时，在执行操作节点 $N_i$ 中保存必要的输入数据。对于第二个部分，在生成对应的执行操作节点 $N_i$ 后，由于此时的输入数据是前一个初等函数操作得到的输出数据，因此其保存了前一个初等函数操作生成的执行操作节点 $N_{i-1}$。因此，我们只需将其输入数据保存的执行操作节点 $N_{i-1}$ 提取出来，然后将当前的执行操作节点 $N_{i}$ 指向 $N_{i-1}$，即可实现节点之间的连接的构建。通过这两个步骤的交替进行，即可实现最终的计算图的构建。例如，在执行加法操作 $(x^2 + y)$ 时，首先执行加法操作获得输出 $t$；然后生成一个对应的加法执行操作节点，即AddBackward0实例 $N_A$，并将 $N_A$ 保存在 $t$ 的.grad_fn属性上；接着提取输入 $x^2$ 和 $y$ 保存的前一个初等函数操作生成的执行操作节点N_x2 = x^2.grad_fn和N_y = y.grad_fn，然后将 $N_A$ 指向 $N_x2$ 和 $N_y$，可以将 $N_x2$ 和 $N_y$ 存储在 $N_A$ 的.next_functions属性内，即N_A.next_functions = [N_x2, N_y]。这样，在整个 forward 过程之后，整个计算图便构建完成；而整个计算图的起始节点便在模型的输出数据output的.grad_fn属性上，在 backward 时便可使用output提取出计算图的起始节点执行反向梯度计算。

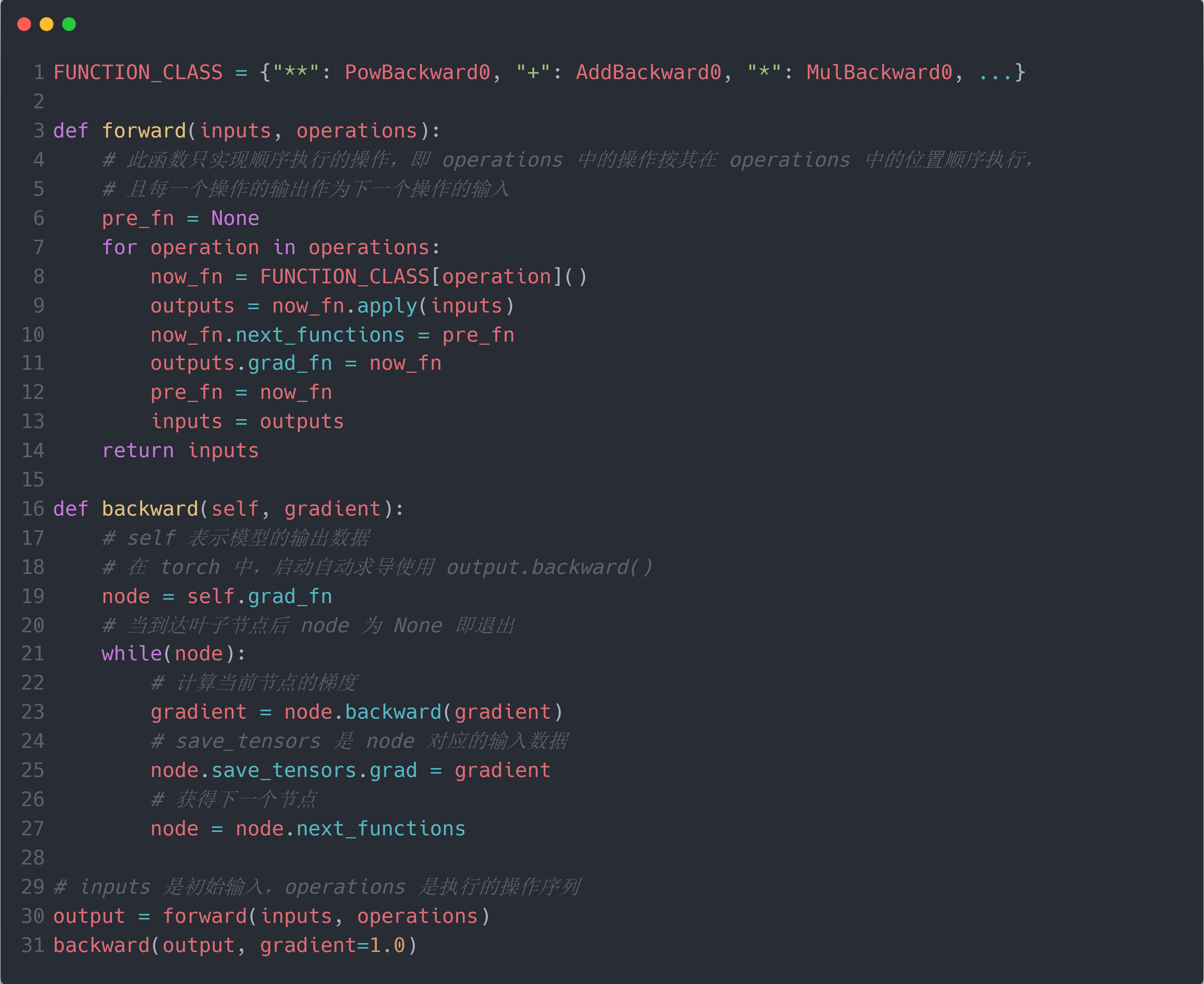
因此，PyTorch 中的模型训练范式为: 在 forward 时，输入数据和模型参数，对于每一个执行操作，构建一个对应的Function实例，并调用.apply()输出结果作为下一个执行操作的输入数据，并将Function实例保存在输出结果的.grad_fn属性上，最终得到模型输出l。而在 backward 时，首先使用fn = l.grad_fn确定输出节点的Function实例（即起始节点），然后调用其.backward()计算对于输入数据的 gradient，接着提取fn的.next_functions属性来获得下一个节点fn=fn.next_functions，并将 gradient 结果传递给下一个节点，即前一个节点的输入数据所对应的Function实例。重复上述操作，直到达到 DAG 的叶子节点，表明 gradient 已计算到输入数据/模型参数。此时，将最终计算得到的 gradient 保存到其.grad属性中。可以看到，默认情况下，PyTorch 不保存中间计算结果的 gradient (即中间结果的.grad属性为None)。下图为一个简单的 PyTorch 中的模型训练范式的代码实现：

一些其他的知识点

此外，PyTorch 的求导是通过计算雅可比矩阵(Jacobian matrix) $J$ 和向量 $\vec{v}$ 的乘积来实现链式法则的反向传播(back propagate)，即：

因此.backward()理论上只能对数求导，不能对向量求导，即 $l.backward()$ 中 $l$ 理论上只能是一个数 (即标量)。为了实现向量 $Q$ 的求导，需要添加与 $Q$ 形状相同的初始梯度Q.backward(gradient = init_gradient)。

同时，PyTorch 的计算图是在每次 forward 时构建的，在 backward 后销毁(只是弃用)；然后在下一次 forward 时再次构建。这样可以保证每次 forward 时的计算图都是最新的，使得可以针对模型进行任意的改动(比如训练前半段更新全部参数，训练后半段更新指定参数)。

下面的代码更为详细地实现了torch.autograd关于模型训练的过程，包括前向构建计算图并计算出模型输出；利用计算图反向传播并存储梯度。

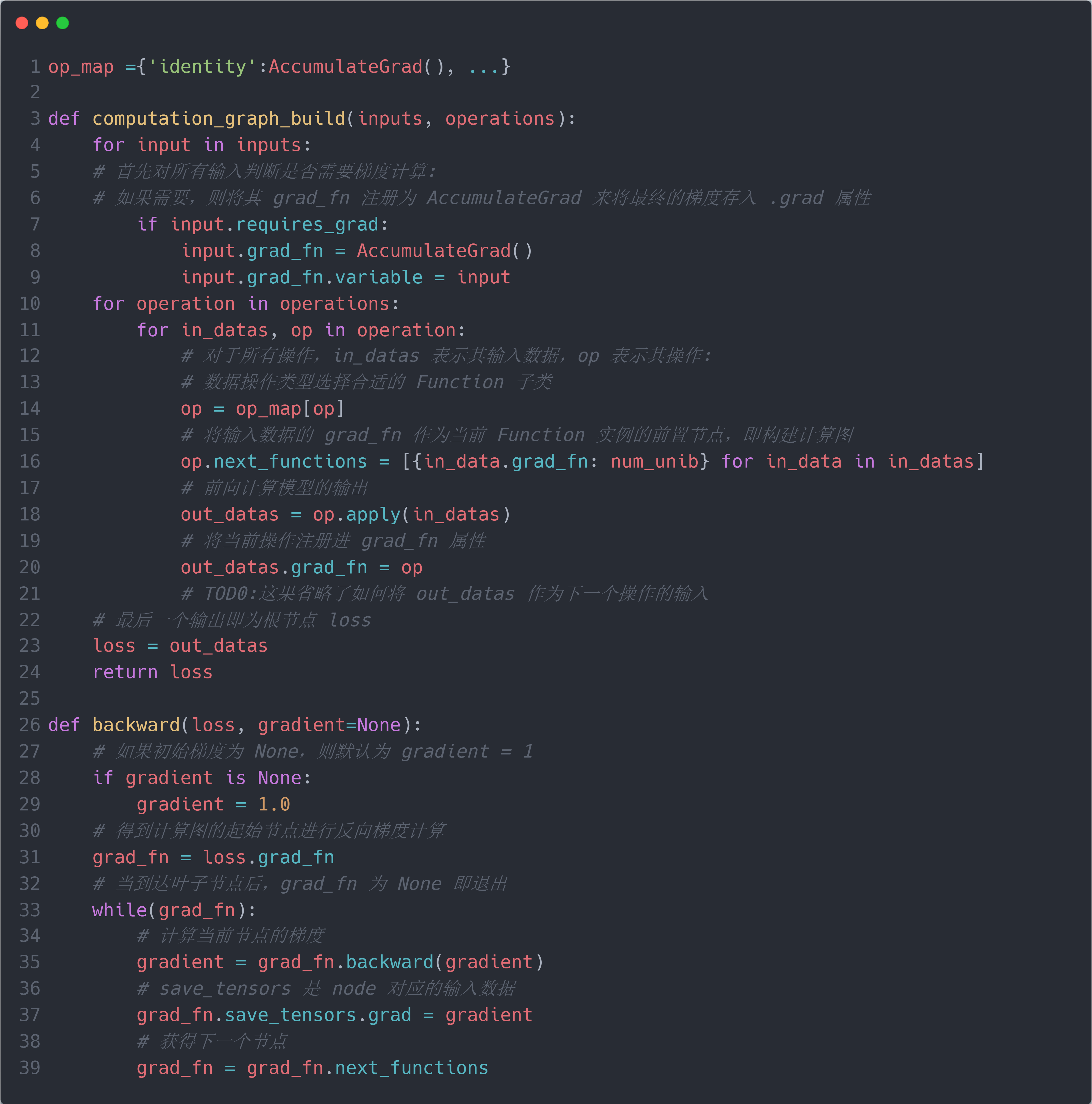
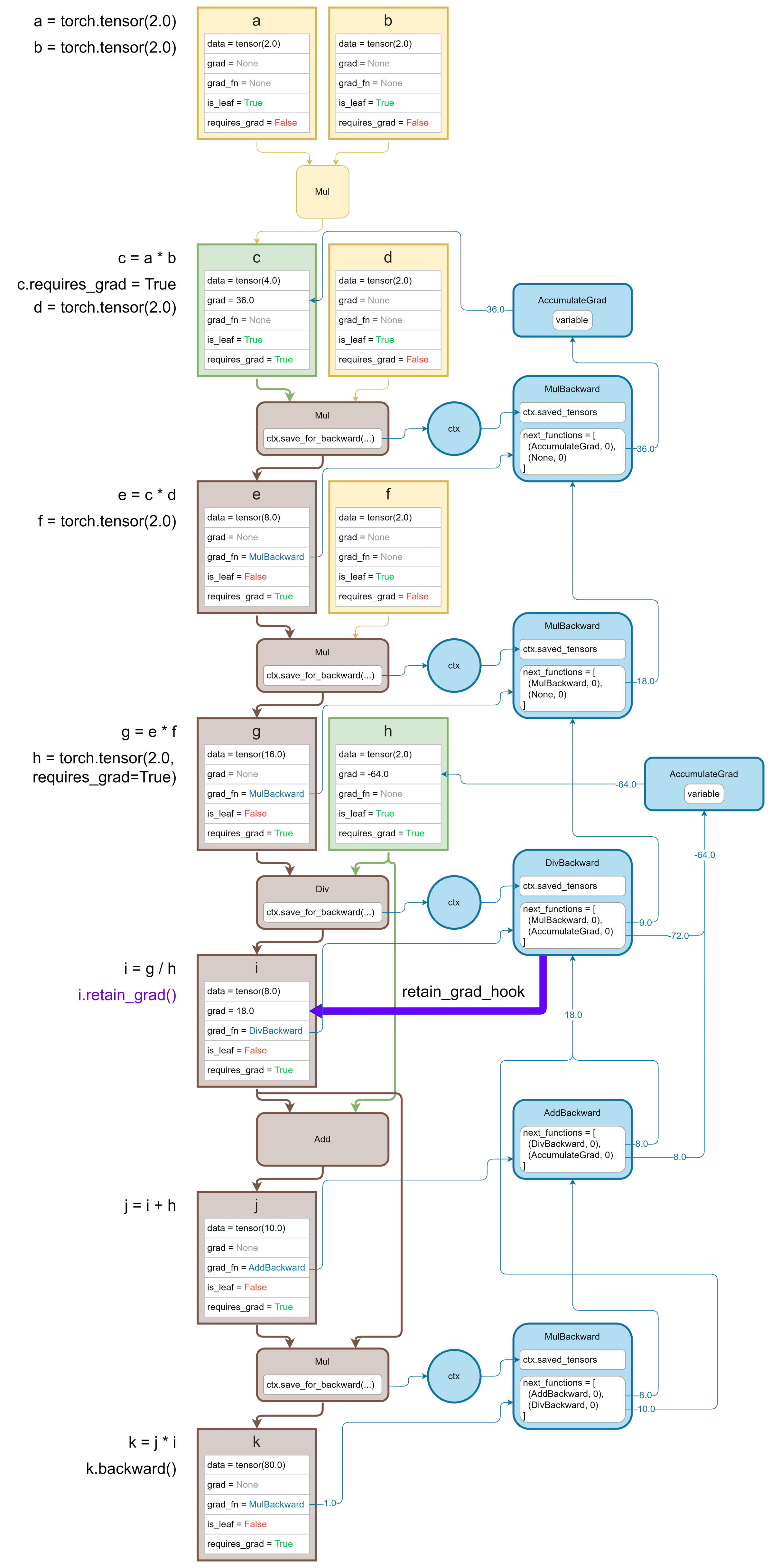
下图展示了一个torch.autograd构建计算图的实例，其中黄色节点表示无需计算梯度的输入数据； 绿色节点表示计算图的叶子节点对应的数据；褐色节点表示中间计算节点所对应的数据；蓝色节点表示torch.autograd构建的计算图：

References

1. Pytorch Autograd In-Deep Introduction Video
2. A Gentle Introduction to torch.autograd
3. Autograd Mechanics
4. Pytorch Autograd API Documentation