The Basic Knowledge of Gradient Penalty
Published:
这篇博客主要讲解了使用梯度惩罚(gradient penalty)作为正则化项来促进模型学习的数学原理和具体实现。
我们知道,最常见的关于参数的正则化是将参数 $\mathcal{W}$ 的 $L_1/L_2$ 作为正则化项加入到 loss 中以限制模型的复杂性。 在 PyTorch 中可以通过设置优化器中的weight_decay参数来实现。 本文介绍的梯度惩罚与其稍有不同,它是利用梯度作为正则化项来促进模型的学习以获得更好的性能(但是不能保证模型的简单性)。 它主要包括 $2$ 中方式:数据梯度惩罚和参数梯度惩罚。下面将详细介绍:
数据梯度惩罚:在深度学习中,存在一种”对抗样本“,它仅仅是在原始样本的基础上添加一些我们难以察觉的随机噪声,便可使模型的结果错误。 典型例子如下:

为了缓解这种情况,就需要构造”对抗样本“给模型学习,来增强模型的鲁棒性,即对抗训练。 具体而言,假设原始样本为 $x$,”对抗样本“为 $x+\Delta x$,其中,$\Delta x$ 是随机噪声, 其要求是范围有限(不然就不能和原始样本看起来相似),并且需要使模型的结果越差越好。 在具体实现时,限制 $\Delta x$ 的范围可以使用限制其的 $L_1$ 范数:$||\Delta x|| \leq \epsilon$,其中 $\epsilon$ 是一个很小的正数; 而衡量模型的结果可以使用损失函数 $\mathcal{L}(x,y;\theta)$,其中 $y$ 表示数据标签,$\theta$ 表示模型参数。 要想加入 $\Delta x$ 后模型结果最差,即使得损失函数值最高:$\underset{\Delta x \in \Omega}{max}{\mathcal{L}(x+\Delta x,y;\theta)}$。 通过求解满足这 $2$ 个条件的 $\Delta x$,便可获得原始样本为 $x$ 的”对抗样本“ $x+\Delta x$。 然后将其送入模型进行训练,使得模型对其标签 $y$ 预测尽可能正确,即使得损失函数最小:$\underset{\theta}{min}{\mathcal{L}(x+\Delta x,y;\theta)}$。 最后通过对每个样本都构造”对抗样本“进行学习,即可完成对抗训练。因此,最终对抗训练的表达式如下:
\[\underset{\theta}{min}\mathbb{E}_{(x,y) \sim \mathcal{D}}\underset{\Delta x \in \Omega; ||\Delta x|| \leq \epsilon}{max}{\mathcal{L}(x+\Delta x,y;\theta)}\]其中 $\mathcal{D}$ 表示训练数据集。那么如何计算 $\Delta x$?其目的是增大损失函数 $\mathcal{L}(x,y;\theta)$,即梯度增加的方向, 因此可以简单地取 $\Delta x = \triangledown_x \mathcal{L}(x,y;\theta)$。注意:这里的梯度是关于数据 $x$ 的梯度,而不是关于参数 $\theta$ 的梯度。 同时为了限制 $\Delta x$ 的范围,需要对其归一化处理,最终可得:
\[\Delta x = \epsilon \dfrac{\triangledown_x \mathcal{L}(x,y;\theta)}{||\triangledown_x \mathcal{L}(x,y;\theta)||}\]因此,对抗训练的最终算法如下:
先使用数据集 $\mathcal{D}$ 训练一个初始模型 $\mathbf{M}_\theta: \underset{\theta}{min}{\mathcal{L}(x,y;\theta)}$;
然后对于数据集 $\mathcal{D}$ 中的每个样本 $\{x_i, y_i\}$,构造”对抗样本“ $\{x_i+\Delta x, y_i\} = \{x_i + \epsilon \dfrac{\triangledown_x \mathcal{L}(x,y;\theta)}{||\triangledown_x \mathcal{L}(x,y;\theta)||}, y_i\}$;
接着使用构造的”对抗样本“继续训练模型 $\mathbf{M}_\theta = \underset{\theta}{min}\mathbb{E}_{(x,y) \sim \mathcal{D}}{\mathcal{L}(x+\Delta x,y;\theta)}$;
循环 $2,3$ 步直至收敛。
回看步骤 $3$ 的对抗训练损失:$\mathcal{D}{\mathcal{L}(x+\Delta x,y;\theta)}$。 由于 $\Delta x$ 很小,将其进行泰勒一阶展开可得:
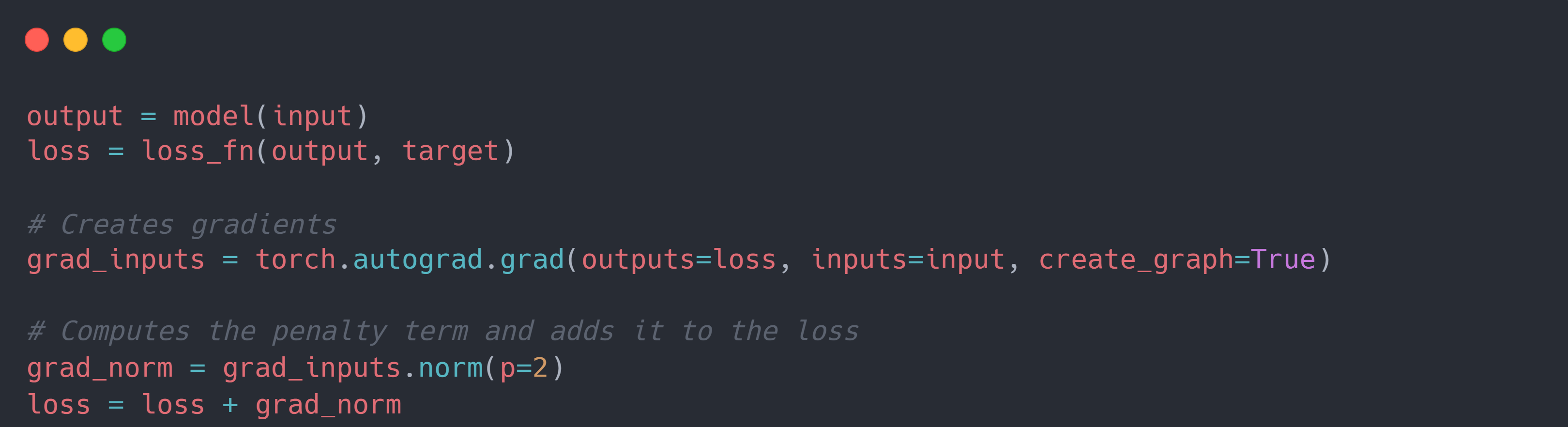
\[\begin{align}\mathcal{L}(x+\Delta x,y;\theta) & = \mathcal{L}(x,y;\theta)+\triangledown_x\mathcal{L}(x,y;\theta)\Delta x \\ & = \mathcal{L}(x,y;\theta)+\triangledown_x\mathcal{L}(x,y;\theta) \times \epsilon \dfrac{\triangledown_x \mathcal{L}(x,y;\theta)}{||\triangledown_x \mathcal{L}(x,y;\theta)||} \leftarrow \color{green}{\Delta x = \epsilon \dfrac{\triangledown_x \mathcal{L}(x,y;\theta)}{||\triangledown_x \mathcal{L}(x,y;\theta)||}}\end{align}\] \[\begin{align}\triangledown_\theta\mathcal{L}(x+\Delta x,y;\theta) & = \triangledown_\theta(\mathcal{L}(x,y;\theta)+\triangledown_x\mathcal{L}(x,y;\theta)\Delta x) \\ & = \triangledown_\theta\mathcal{L}(x,y;\theta)+\triangledown_\theta\triangledown_x\mathcal{L}(x,y;\theta) \times \epsilon \dfrac{\triangledown_x \mathcal{L}(x,y;\theta)}{||\triangledown_x \mathcal{L}(x,y;\theta)||} \\ & = \triangledown_\theta\mathcal{L}(x,y;\theta)+\triangledown_\theta(\color{red}{\triangledown_x\mathcal{L}(x,y;\theta)} \times \epsilon \dfrac{\triangledown_x \mathcal{L}(x,y;\theta)}{\color{red}{||\triangledown_x \mathcal{L}(x,y;\theta)||}}) \\ & = \triangledown_\theta\mathcal{L}(x,y;\theta)+\triangledown_\theta(\epsilon||\triangledown_x\mathcal{L}(x,y;\theta)||) \\ & = \triangledown_\theta(\mathcal{L}(x,y;\theta) + \epsilon||\triangledown_x\mathcal{L}(x,y;\theta)||)\end{align}\]也就是说,对抗训练相当于往原始的损失函数添加样本的梯度作为”惩罚项“。这便是关于数据的梯度惩罚,其主要目的是为了增强模型对于输入的鲁棒性。 在具体的 PyTorch 代码实现中,可以参考如下代码框架:
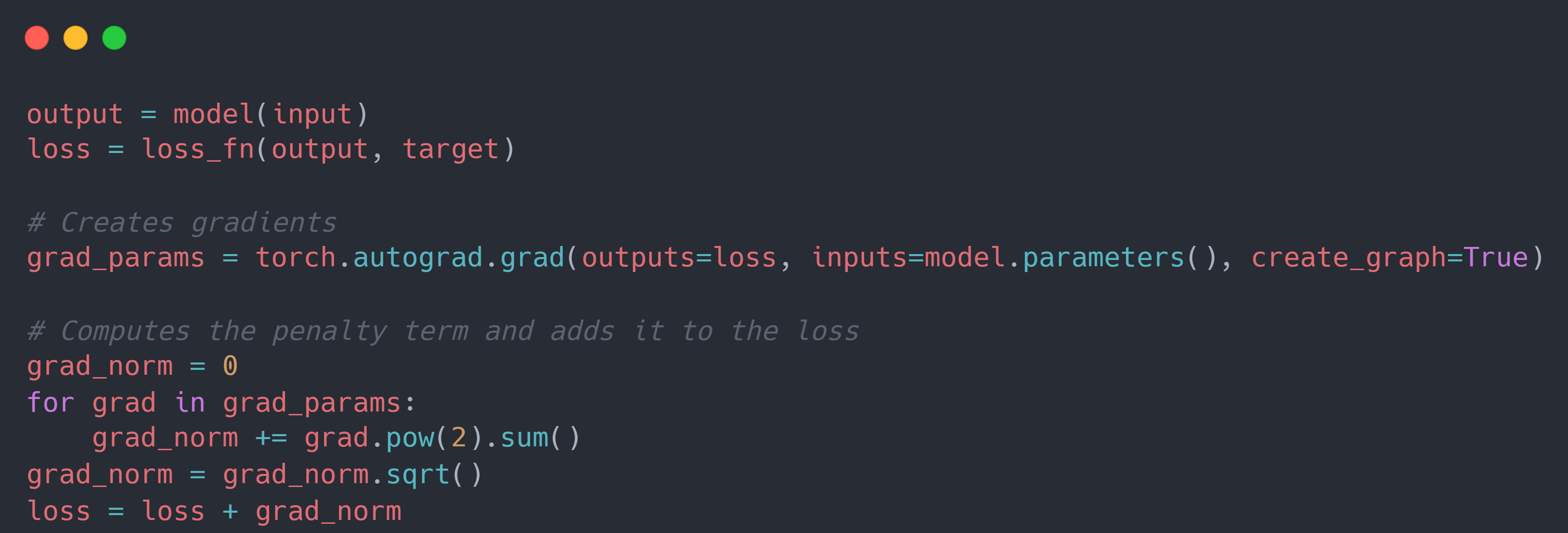
参数梯度惩罚:我们在训练模型参数时,一般通过梯度下降法进行学习,即 $\theta_{i+1} = \theta_i - \gamma\triangledown_\theta\mathcal{L}(·,·;\theta_i)$。 如果 $\gamma$ 足够小,则 $\theta$ 的更新近似与在连续时间 $t$ 上,即 $\theta(t)$。在此基础上,将原始损失函数 $\mathcal{\mathcal{L}(·,·;\theta(t))}$ 对 $t$ 进行求导,并使用一阶泰勒展开可得:
\[\frac{d}{dt}{\mathcal{\mathcal{L}(·,·;\theta(t))}} = \tilde{\triangledown}_\theta\mathcal{L}(·,·;\theta(t)) \times \dfrac{d\theta_t}{dt}\]我们希望损失函数 $\mathcal{L}$ 关于 $t$ 的下降最快,在 $\theta_t'=\dfrac{d\theta}{dt}$ 的模长固定的情况下,即取梯度负方向进行计算可以使得 $\frac{d}{dt}{\mathcal{\mathcal{L}(·,·;\theta(t))}}$ 最大,即:
\[\dfrac{d\theta_t}{dt} = - \color{orange}{\tilde{\triangledown}_\theta\mathcal{L}(·,·;\theta(t))} \leftarrow \underset{\theta_t'}{max}\frac{d}{dt}{\mathcal{\mathcal{L}(·,·;\theta(t))}}\]因此,只需求解上述的常微分方程,即可求解得到最优值的 $\theta$。求解常微分方程最常用的方法即是常微分求解器,它们的主要思路都是通过将常微分方程转化为差分方程进行逐步迭代的方法来近似最优解。 以最简单的欧拉求解器为例,其迭代公式为:
\[\theta_{t + \gamma} = \theta_{t} - \gamma \times \color{orange}{\triangledown_\theta\mathcal{L}(·,·;\theta_t)}\]但是与原始常微分方程的最优解相比差分方程求解得到的最优解与其有一定的偏差,减轻这种偏差的最直接的方法是在利用差分方程求解得到的最优解的前提下, 反向加上偏差来得到原始常微分方程的最优解。由于常微分方程和差分方程都是利用梯度进行计算,因此只需求解梯度的偏差即可, 即 $\color{orange}{\tilde{\triangledown}_\theta\mathcal{L}(·,·;\theta(t))}$ 与 $\color{orange}{\triangledown_\theta\mathcal{L}(·,·;\theta_t)}$ 的偏差。 那么偏差如何计算?将 $\theta_{t+\gamma}$ 进行泰勒展开:
\[\begin{align}\theta_{t + \gamma} & = \theta_t + \gamma \times \theta_t' + \dfrac{1}{2} \gamma^2 \times \theta_t'' + ... \\ & = (1 +\gamma D + \dfrac{1}{2}\gamma^2D^2 + ...)\theta_t = e^{\gamma D}\theta_t; D = \dfrac{d}{dt}\end{align}\] \[\begin{align}e^{\gamma D}\theta_t & = \theta_{t} - \gamma \times \triangledown_\theta\mathcal{L}(·,·;\theta_t) \leftarrow \color{green}{\theta_{t + \gamma} = e^{\gamma D}\theta_t}; \color{green}{\theta_{t + \gamma} = \theta_{t} - \gamma \times \triangledown_\theta\mathcal{L}(·,·;\theta_t)} \\ (e^{\gamma D}-1)\theta_t & = - \gamma \times \triangledown_\theta\mathcal{L}(·,·;\theta_t) \\ D\theta_t = \theta_t' & = -\gamma \big(\dfrac{D}{e^{\gamma D}-1}\big) \times \triangledown_\theta\mathcal{L}(·,·;\theta_t) \\ & = -\big(1 - \dfrac{1}{2}\gamma D + ...) \times \triangledown_\theta\mathcal{L}(·,·;\theta_t) \\ & \approx -\big(1 - \dfrac{1}{2}\gamma D) \times \triangledown_\theta\mathcal{L}(·,·;\theta_t) \\ & = -\triangledown_\theta\mathcal{L}(·,·;\theta_t) + \dfrac{1}{2}\gamma D \triangledown_\theta\mathcal{L}(·,·;\theta_t) \\ & = -\triangledown_\theta\mathcal{L}(·,·;\theta_t) + \dfrac{1}{2}\gamma \triangledown_\theta\triangledown_\theta\mathcal{L}(·,·;\theta_t)\theta_t' \leftarrow \color{red}{\dfrac{d}{dt}{\triangledown_\theta\mathcal{L}(·,·;\theta_t)} = \dfrac{d}{d\theta}{\triangledown_\theta\mathcal{L}(·,·;\theta_t)} \times \dfrac{d}{dt}\theta_t}\\ & = -\triangledown_\theta\mathcal{L}(·,·;\theta_t) + \dfrac{1}{2}\gamma \triangledown_\theta\triangledown_\theta\mathcal{L}(·,·;\theta_t)\big[\color{green}{-\triangledown_\theta\mathcal{L}(·,·;\theta_t) + \dfrac{1}{2}\gamma \triangledown_\theta\triangledown_\theta\mathcal{L}(·,·;\theta_t)\theta_t'}\big] \\ & = -\triangledown_\theta\mathcal{L}(·,·;\theta_t) - \dfrac{1}{2}\gamma \triangledown_\theta\triangledown_\theta\mathcal{L}(·,·;\theta_t) \times \triangledown_\theta\mathcal{L}(·,·;\theta_t) \leftarrow \color{red}{\dfrac{1}{2}\gamma \triangledown_\theta\triangledown_\theta\mathcal{L}(·,·;\theta_t)\theta_t' \times \dfrac{1}{2}\gamma \triangledown_\theta\triangledown_\theta\mathcal{L}(·,·;\theta_t)\theta_t' \approx 0}\\ & = -\triangledown_\theta\mathcal{L}(·,·;\theta_t) - \dfrac{1}{4}\gamma \triangledown_\theta||\triangledown_\theta\mathcal{L}(·,·;\theta_t)||^2 \\ -\tilde{\triangledown}_\theta\mathcal{L}(·,·;\theta_t) & = -\triangledown_\theta\mathcal{L}(·,·;\theta_t) - \dfrac{1}{4}\gamma \triangledown_\theta||\triangledown_\theta\mathcal{L}(·,·;\theta_t)||^2 \leftarrow \color{green}{\dfrac{d\theta_t}{dt} = - \tilde{\triangledown}_\theta\mathcal{L}(·,·;\theta_t)} \\ \tilde{\triangledown}_\theta\mathcal{L}(·,·;\theta_t) & = \triangledown_\theta\big(\mathcal{L}(·,·;\theta_t) + \dfrac{1}{4}\gamma \triangledown_\theta||\triangledown_\theta\mathcal{L}(·,·;\theta_t)||^2\big) \end{align}\]可以看到,要想纠正因逐步迭代导致的最优解偏差,相当于往原始的损失函数添加模型参数的梯度作为”惩罚项“。这便是关于参数的梯度惩罚,其主要目的是为了纠正模型使用梯度下降法求解导致的偏差。 在具体的 PyTorch 代码实现中,可以参考如下代码框架: