The Basic Knowledge of Torch Train Pipeline
Update:
Published:
这篇博客主要讲解 PyTorch 训练模型的整个流程的具体细节, 包括如何在前向过程中构建计算图;后向传播过程中如何计算并保存梯度;优化器如何根据梯度更新模型参数。(建议先阅读我之前关于 torch.autograd 的博客 The Basic Knowledge of PyTorch Autograd)
Torch 训练的整体流程
我们以最简单的乘法为例:两个标量 $x_1$ 和 $x_2$ 相乘得到 $v$;然后使用v.backward()函数反向计算 $x_1$ 和 $x_2$ 的梯度;最后使用 SGD 优化器更新 $x_1$ 和 $x_2$。代码如下:

接着我们使用torchviz的make_dot函数获取 PyTorch 构建的计算图:
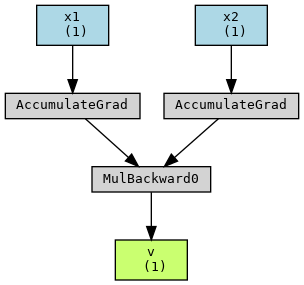
可以看到,计算图的方向与前向计算过程刚好相反。这里,我们将简单描述 Torch 训练的整体流程:在执行乘法过程中,Torch 分别为 $x_1$ 和 $x_2$ 构建一个AccumulateGrad节点,并将 $x_1$ / $x_2$ 存储在对应的AccumulateGrad节点的variable属性中;然后根据*的乘法操作为 $v$ 构建一个MulBackwrad0节点,并将其存储在 $v$ 的grad_fn属性中。
而在后向传播计算梯度的过程中,执行v.backward()函数时,Torch 首先会获取到存储在 $v$ 的grad_fn属性中MulBackwrad0节点,然后将初始梯度gradient作为输入传递给其.backward()函数计算该节点的输入的梯度,即 $x_1$ 和 $x_2$ 的梯度;接着将 $x_1$ 和 $x_2$ 的梯度作为输入传递给各自对应的AccumulateGrad节点的.backward()函数实现将梯度累加到 $x_1$ 和 $x_2$ 的.grad属性中。
在 SGD 优化器更新 $x_1$ 和 $x_2$ 的过程中,SGD 的step()函数遍历初始化时传入的params参数,判断其required_grad属性是否为True,若为True,则取出其data属性和grad属性,将data减去grad,得到更新后的参数params。
前向过程构建计算图
介绍基本知识:Node $\rightarrow$ Edge $\rightarrow$ MulBackward0
叙述过程:Tensor.mul $\rightarrow$ torch._C._TensorBase.__mul__ $\rightarrow$ mul_Tensor $\rightarrow$ collect_next_edges $\rightarrow$ gradient_edge $\rightarrow$ set_next_edges $\rightarrow$ set_history $\rightarrow$ set_gradient_edge
不知道你们有没有这样的疑惑:在我们的代码中,只是简单的编写了两个tensor的矩阵相乘:tensor = tensor1 * tensor2;而 PyTorch 便自动为我们构建了一个计算图(可以看到tensor的.grad_fn属性为MulBackward0;如果tensor1 / tensor2的.required_grad属性为True)。这是如何实现的?虽然我们在前面的博客 The Basic Knowledge of PyTorch Autograd 中讲了关于 PyTorch 自动求导的过程,知道了每个节点是在初等函数执行时立即创建的,但并没有涉及到具体的代码对应过程(即在tensor = tensor1 * tensor2背后究竟是哪些代码实现了计算图的创建)。实际上,PyTorch 在Tensor类中实现了对每个初等函数的重载,使得每个初等函数操作并不只是简单的实现初等函数而已。例如对于mul操作,Tensor类内的重载实现为:
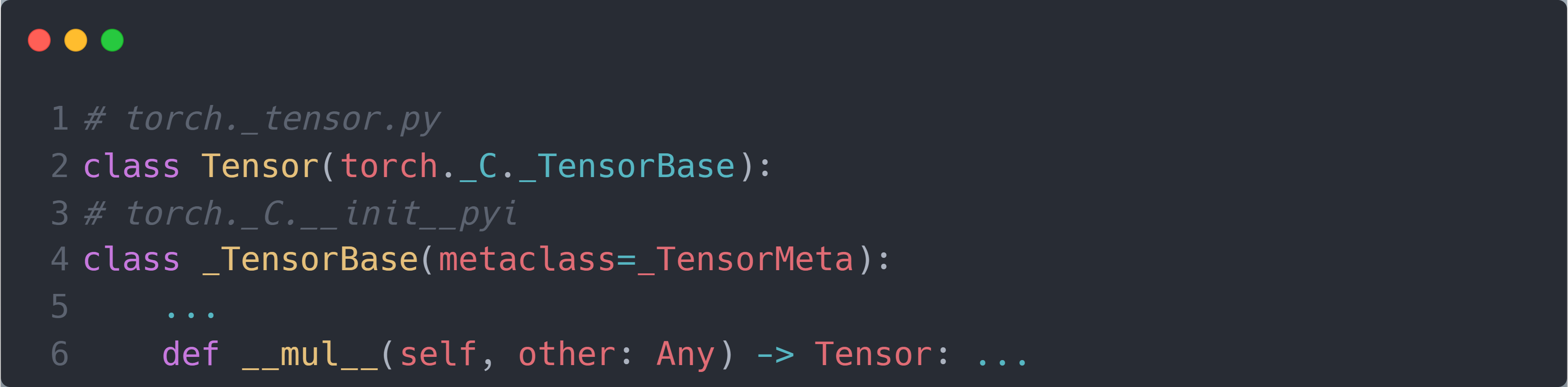
可以看到,其内部实现是使用 C++ 语言来编写的,继续追溯到 C++ 源代码中,可以看到mul操作的具体实现为:
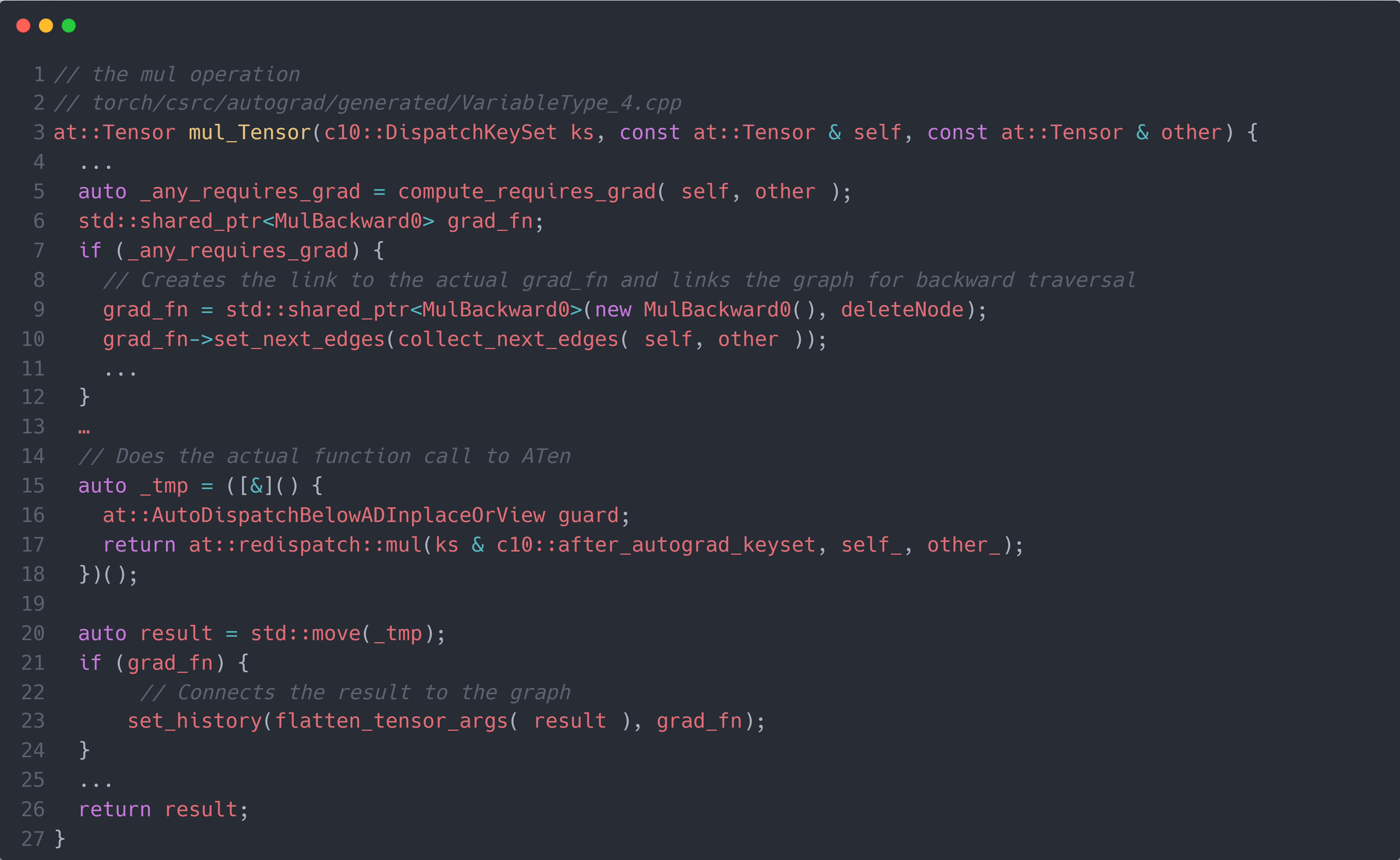
这个代码有点吓人,让我们一步步来。其中,self, other分别是mul操作的第一个tensor和第二个tensor。首先,第 $4$ 行代码的compute_requires_grad()函数判断self/other的required_grad属性是否为True,只要有一个为True,则_any_requires_grad为True,表示此时的mul操作需要生成节点,同时其生成的输出的required_grad也为True。在得到_any_requires_grad为True后(第 $6$ 行代码),代码会创建一个MulBackward0作为该mul操作在计算图上的节点(第 $8$ 行代码),同时将其赋值给grad_fn;而set_next_edges()则是设置当前的MulBackward0节点与之前操作生成的节点的连接。
接下来,让我们继续深入每个部分。首先,self/other是一个Tensor,当设置其required_grad的属性为 True 时,会执行下面的set_requires_grad()函数:
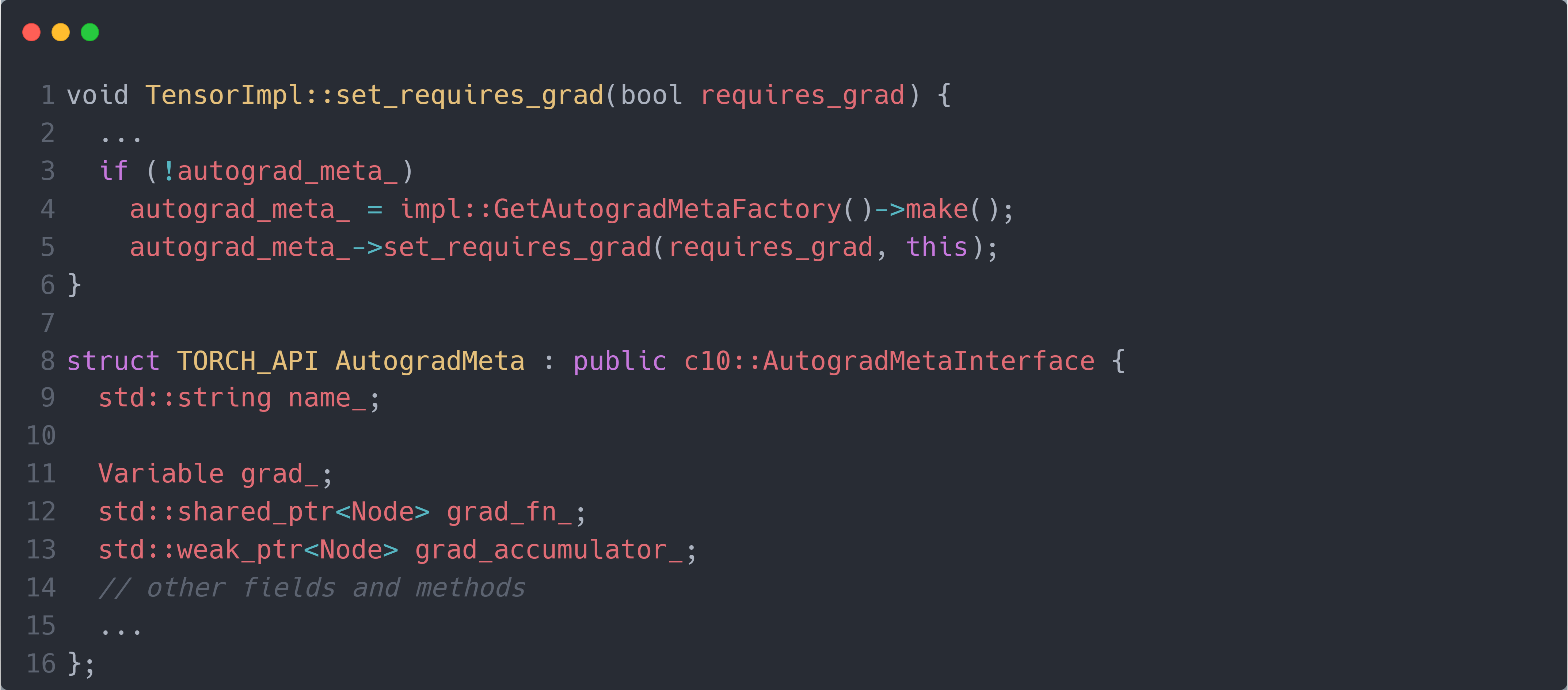
其会为self/other创建一个新的属性autograd_meta_(AutogradMeta类),该属性用于存储self/other的梯度(grad_)和节点(grad_fn_)等),对应于 Python 代码里的.grad和grad_fn属性。(当然其还有梯度累加器(grad_accumulator_用于累加多个父节点传递的梯度)
其次,计算图的每个节点的类型均为Node结构体(对应于 Python 代码中的Function类)。下图是Node结构体的具体内容:

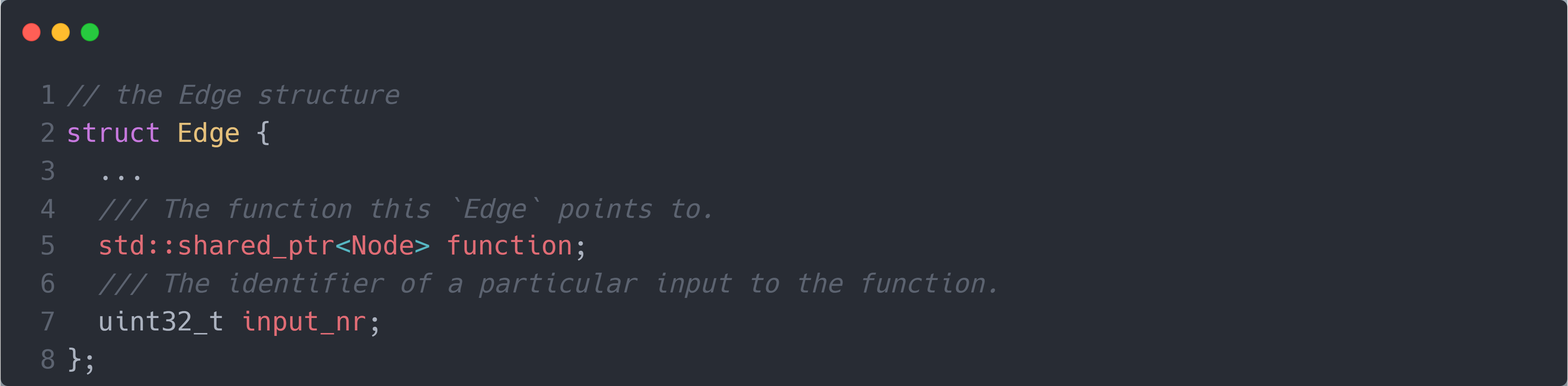
其中,operator()和apply()分别是节点的前向和反向计算函数(对应于 Python 代码中的forward()和backward()函数),不同的节点可以重写它们以实现不同的计算过程。而next_edges_则是存储节点所连接的前向节点(对应于 Python 代码中的next_functions)。因此,next_edges_中的每条边都是Edge结构体,结构体中存储执行前向节点的指针。下图是Edge结构体的具体内容:
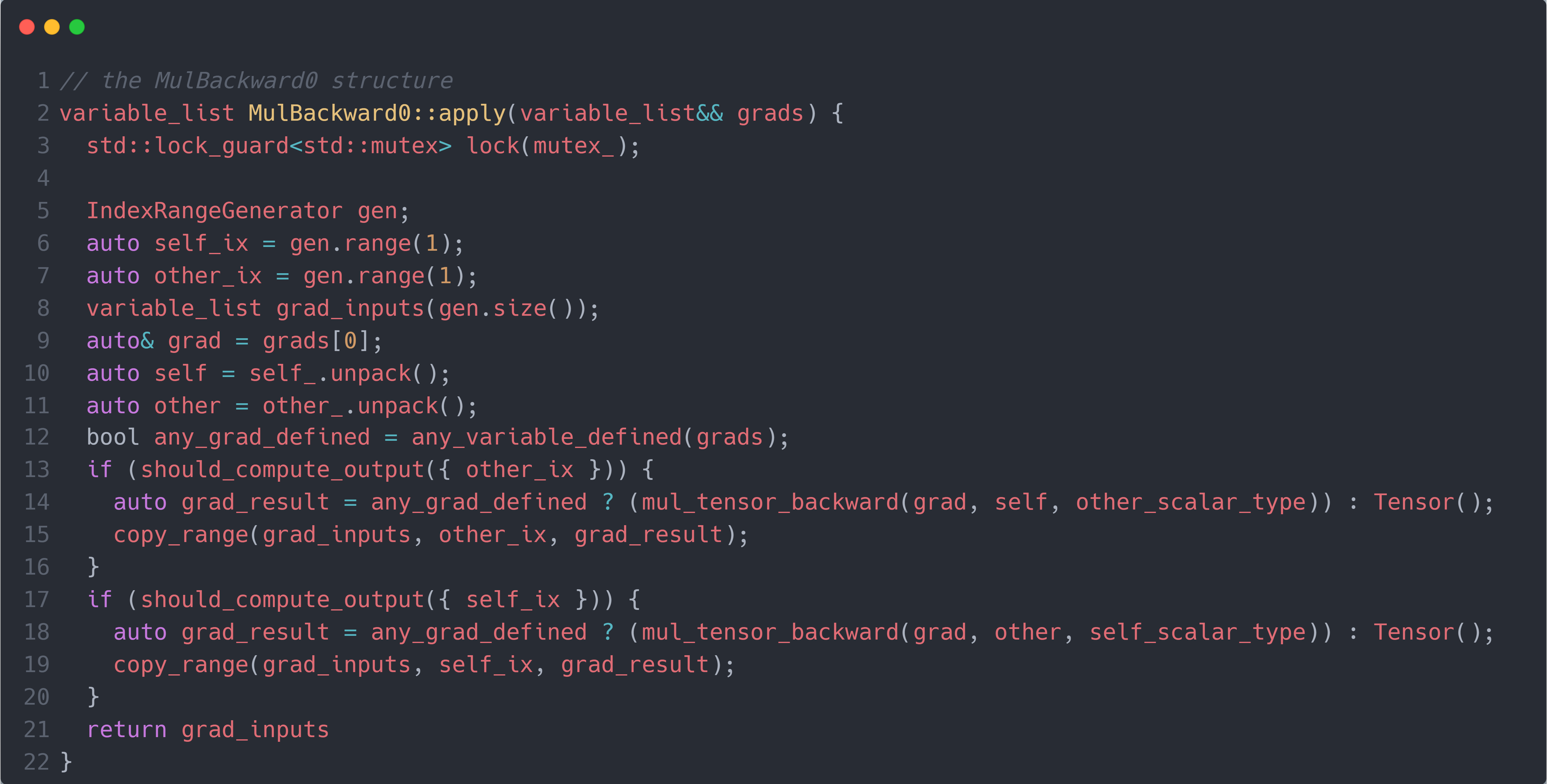
所以,mul_Tensor()函数中的MulBackward0操作即是Node结构体的子结构体,其主要重写了apply()方法用于计算mul操作的反向过程(其没有重写operator()方法,因为mul操作的前向过程在mul_Tensor()函数中实现),如下图所示:
了解了各个变量的基本结构后,我们回到mul_Tensor()函数中。可以猜到,set_next_edges()应该是要将之前操作生成的节点赋值到当前的MulBackward0节点的next_edges_中。首先需要获取之前操作生成的节点,通过collect_next_edges()函数实现。如下图所示:
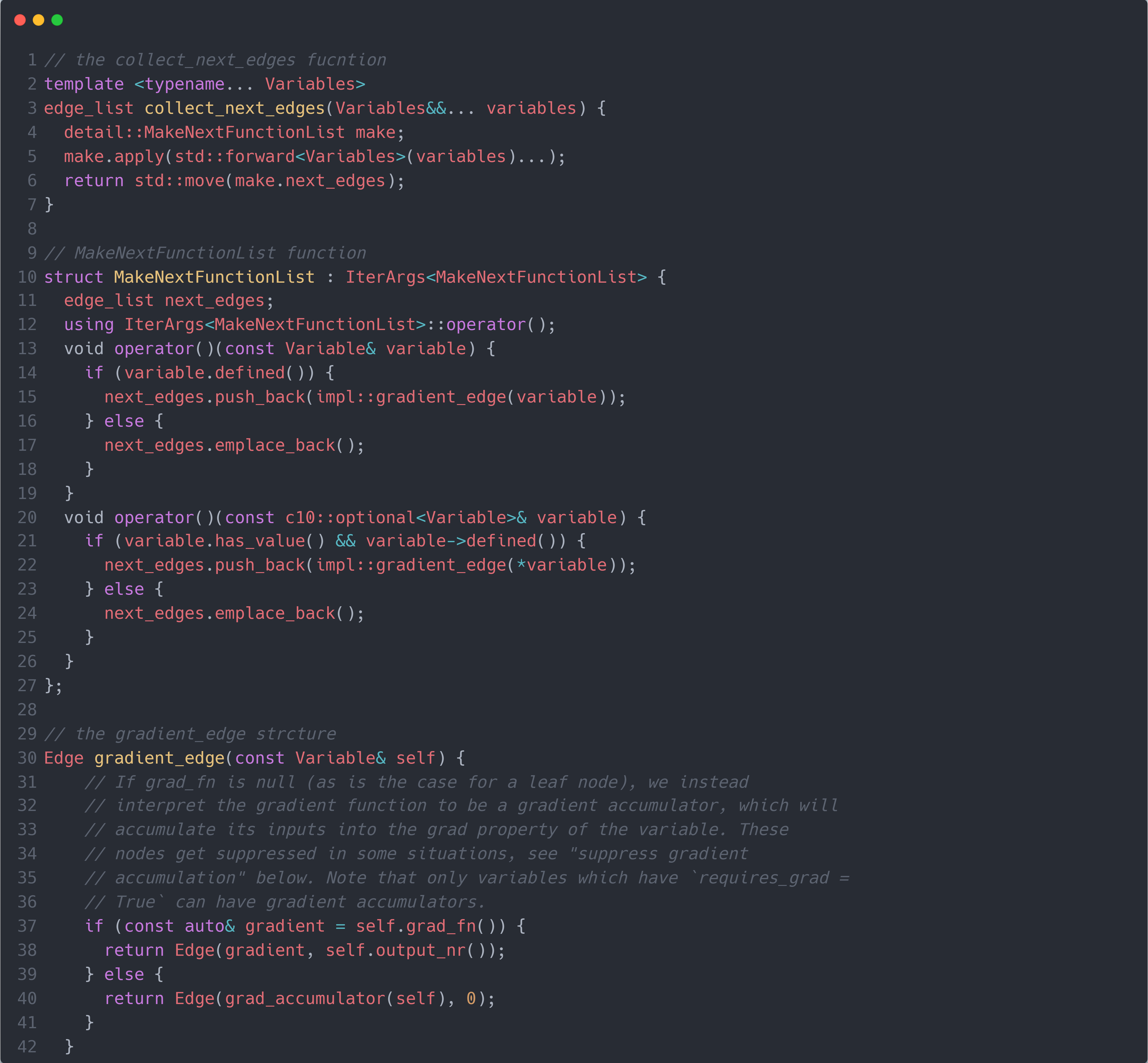
这个代码更吓人,还是让我们一步步来!首先,collect_next_edges()函数是通过输入mul操作的输入数据,即self, other;然后创建MakeNextFunctionList结构体的实例make,并调用其apply()方法(即MakeNextFunctionList的operator()方法)实现的获取之前操作生成的节点。而MakeNextFunctionList的operator()方法同样输入mul操作的输入数据,然后构建next_edges数组,接着通过调用gradient_edge()方法获取每个输入数据里保存的之前操作生成的节点(使用Edge结构体包装),并将其存储在next_edges数组中,最后将next_edges数组返回给collect_next_edges()函数。而gradient_edge()方法输入mul操作的输入数据,判断其是否保存的之前操作生成的节点gradient = self.grad_fn():若有,则说明该输入数据属于中间数据,则将其包装成Edge结构体后返回;若没有,则说明该输入数据属于最原始的输入数据,则将其保存的节点设置为AccumulateBackward节点(通过调用grad_accumulator()函数获得),并其包装成Edge结构体后返回(这就是为什么每个叶子节点前都有一个AccumulateBackward节点的原因)。从gradient_edge()方法返回到MakeNextFunctionList的operator()方法,再返回到collect_next_edges()函数,即可得到当前的MulBackward0节点的之前操作生成的节点。然后通过set_next_edges()将其赋值到next_edges_中。如下图所示:

完成了在set_next_edges()后,接下来便需要计算前向过程(对应于 Python 代码中的Function类的forward()方法),获得计算结果result(mul_Tensor()函数中的第 $15 \sim 20$ 行)。
最后,需要将生成的MulBackward0节点保存到输出result中(对应 Python 代码的outputs.grad_fn = now_fn),其通过set_history()函数实现。如下图所示:
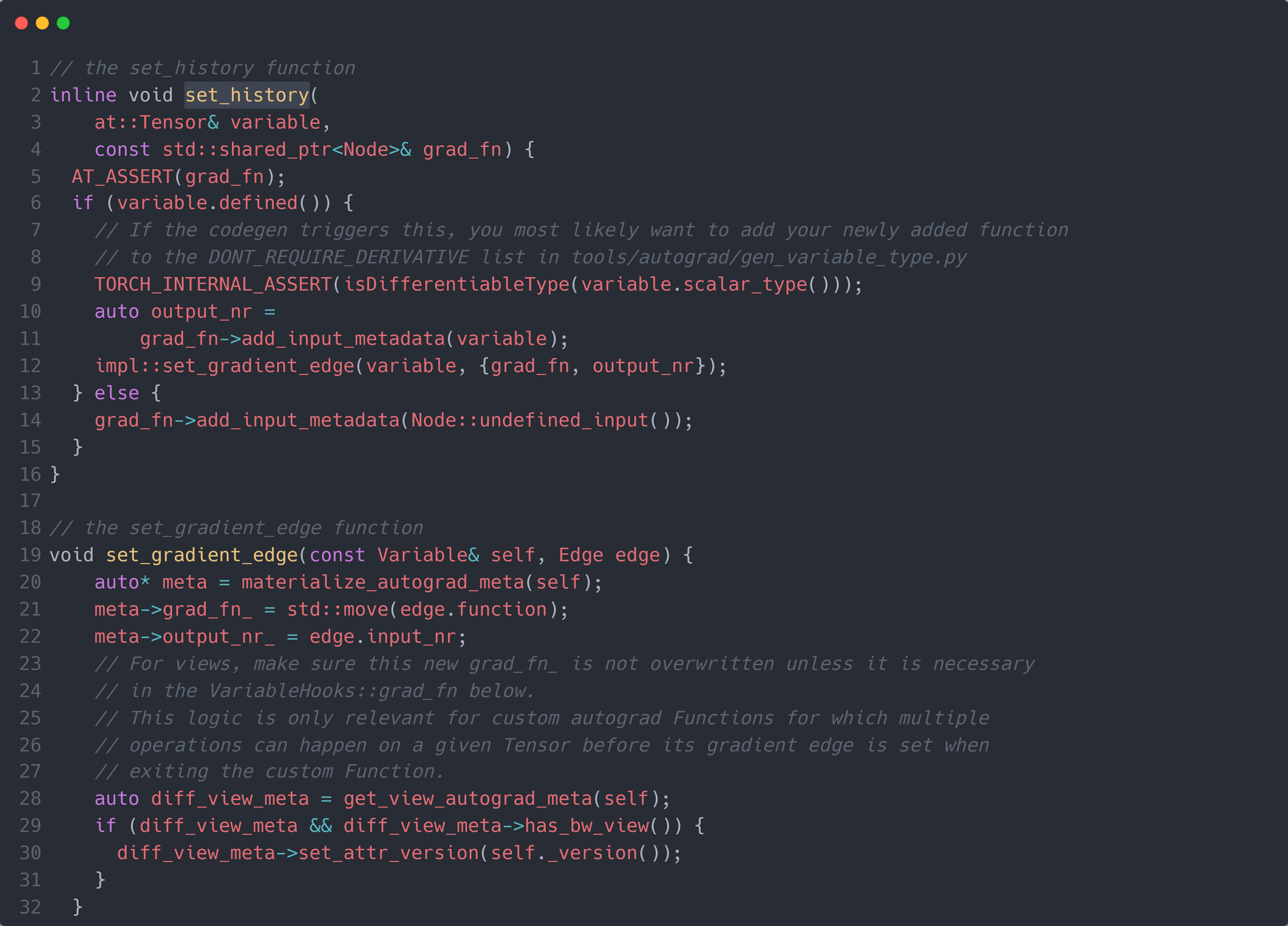
首先,set_history()函数是通过输入前向过程的输出result和生成的MulBackward0节点,然后调用set_gradient_edge()方法实现的将MulBackward0节点保存在输出result的AutogradMeta属性的grad_fn_中。而set_gradient_edge()方法则是通过输入同样的前向过程的输出result和生成的MulBackward0节点,取出result的AutogradMeta属性meta,将MulBackward0赋值在其grad_fn_属性中。
至此,我们终于“稍微”搞懂了 PyTorch 自动化构建计算图的过程。原来在我们写了一个简单的tensor = tensor1 * tensor2代码背后,PyTorch 执行了如此多的额外代码操作来实现计算图的构建。
后向传播过程计算并保存梯度
敬请期待!
优化器根据梯度更新模型参数
不同于前向过程和后向过程,其代码需要深入到底层的 C++ 源代码进行理解,优化器利用计算得到的梯度更新模型参数的过程主要在 Python 源代码中实现。现在让我们以最简单的 SGD 优化器为例:首先我们需要初始化一个 SGD 优化器实例,它至少需要输入两个参数(模型参数params(即 $x_1$ 和 $x_2$)和初始学习率lr),如下图所示:

在经过前向过程(v = x1 * x2)和后向过程(v.backward())后,此时 $x_1$ 和 $x_2$ 的grad属性内已经存储了计算得到的梯度。因此,我们能想到的最直接的做法就是遍历params的每一个参数,判断每个参数的required_grad属性是否为True;若是,则取出其对应的grad属性内存储的梯度,并将该参数与其梯度(乘以学习率)进行相减即可实现参数更新。因此 SGD 类的简单实现应该如下图所示:

但是这里有个问题,前面我们说过,PyTorch 重载了Tensor类的所有初等函数操作;因此,当我们执行param -= grad * self.lr操作时,我们实际上会在原有计算图的基础上再构建一个SubBackward0节点分支,如下图所示:
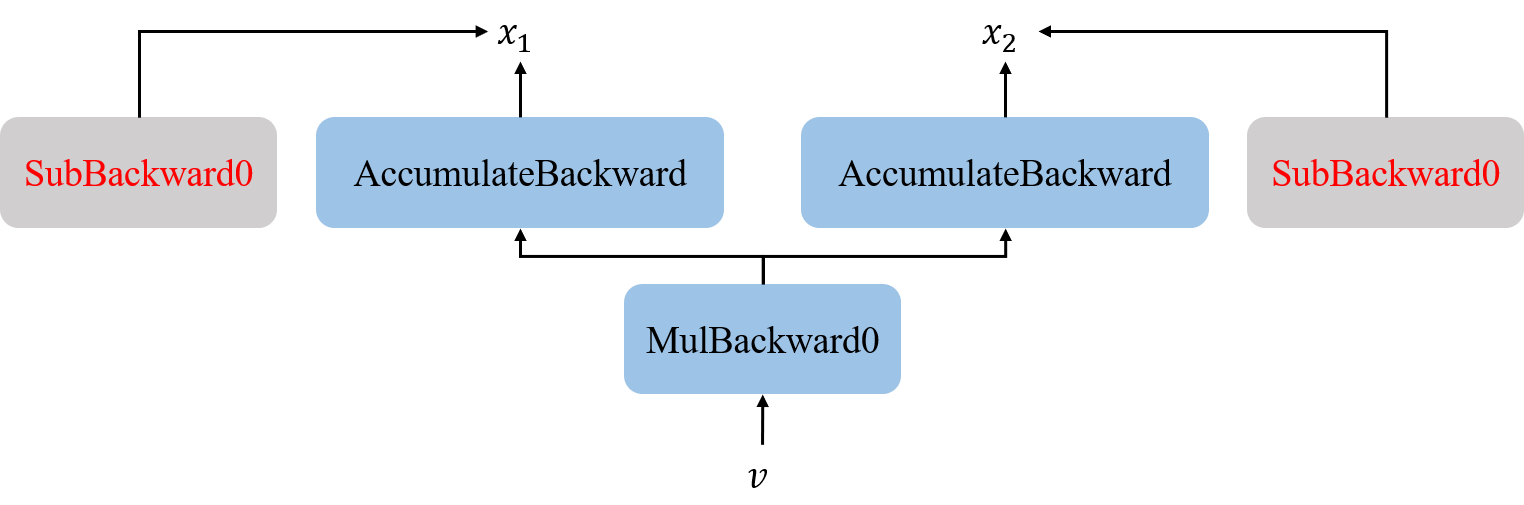
因此,为了不让 PyTorch 继续构建计算图,我们需要设置with torch.no_grad()来“告诉” PyTorch 下面的操作不需要构建计算图,此时Tensor类的所有初等函数操作就不会构建计算图。因此,改进的SGD 类代码如下图所示:

而在 SGD 的源代码中,PyTorch 使用另一种方式来避免计算图的构建,通过使用torch._dynamo.graph_break()实现计算图的脱离来确保初等函数操作就不会继续构建计算图。
了解了如何简单实现 SGD 后,接下来让我们进入 SGD 的源代码来验证我们的实现是否正确。首先是 SGD 如何保存输入进来的params参数,下图为 SGD 的__init__()函数部分代码:
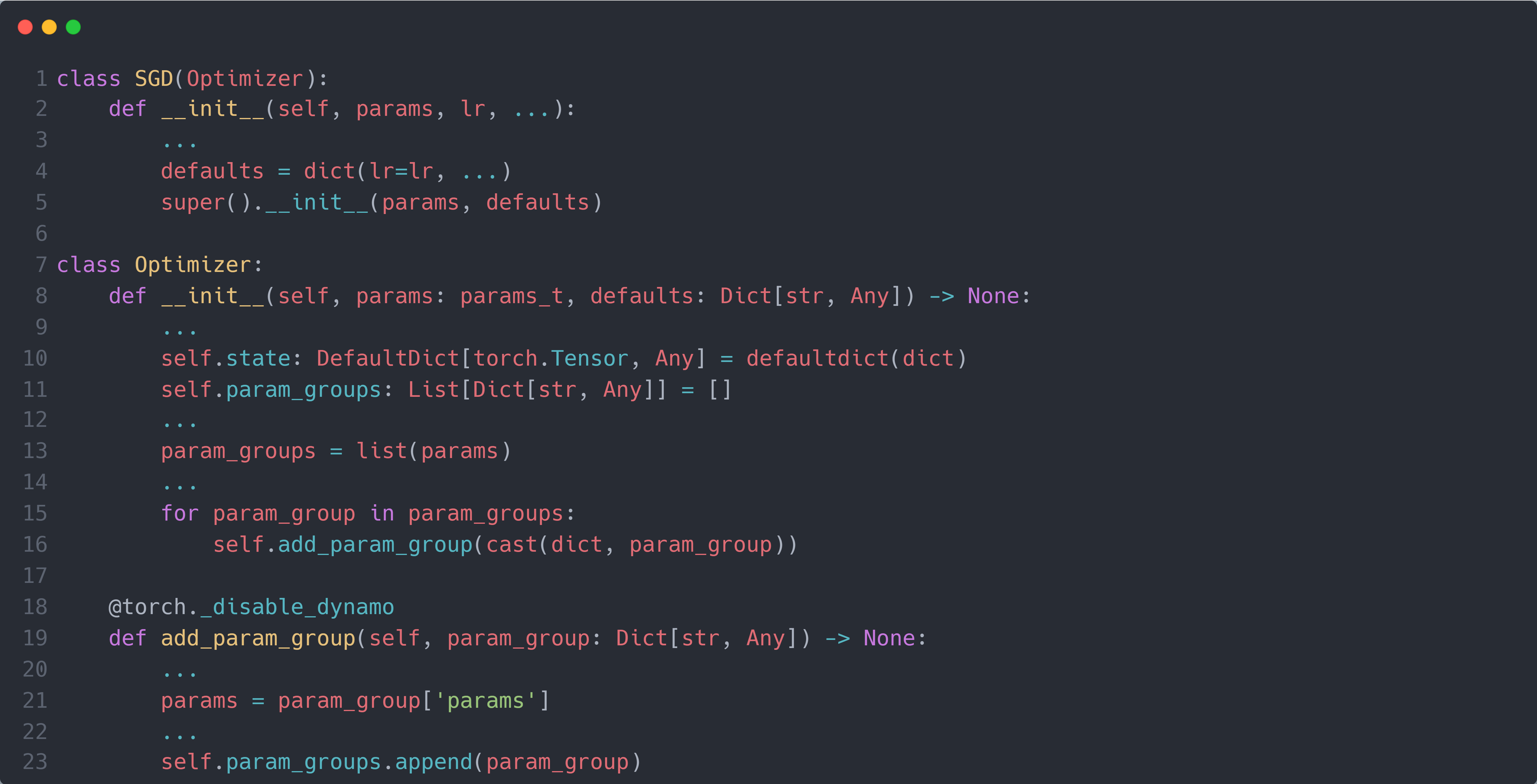
可以看到,SGD 是通过调用其父类Optimizer的__init__()函数将输入进来的参数保存在self.param_groups列表内。接下来就是 SGD 的step()函数,下图为 SGD 的step()函数部分代码:
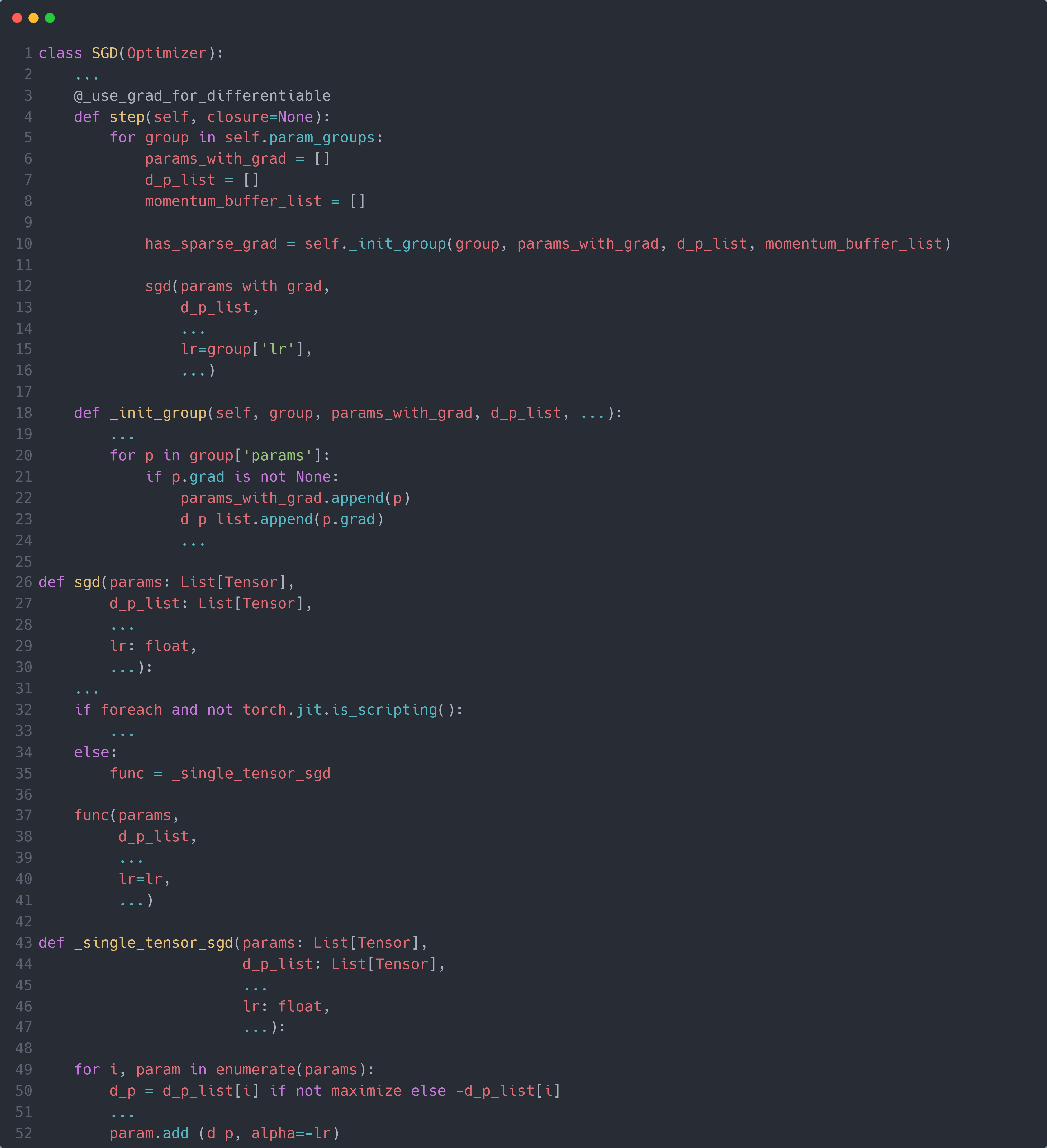
首先,step()函数对每个self.param_groups列表内的每个参数组group,调用self._init_group()判断其每个参数p的grad属性是否为None:如果不是,则表示需要更新该参数,则将其存储在params_with_grad列表中,同时使用d_p_list列表存储其对应的梯度p.grad。
接着,对于那些需要更新的参数params_with_grad,调用sgd()函数进行参数更新。在sgd()函数中,进行一系列的检查后,调用_single_tensor_sgd()函数进行参数更新。 而_single_tensor_sgd()函数则是遍历params_with_grad列表中的所有参数,对于每个参数param列表,取出其在d_p_list列表中的对应的梯度d_p,并使用原地更新的方式进行参数更新:param.add_(d_p, alpha=-lr)。由于是原地更新,且传入优化器的参照即为模型参数,因此对应的模型中的参数也会同步进行更新。
至此,我们终于完成了 PyTorch 训练模型的整个流程的具体细节(深入到底层代码),包括如何在前向过程中构建计算图;
