这篇博客参考了 通俗理解EM算法，详细推导了 Expectation Maximization (EM) 算法。

Preliminary

点估计问题：假设总体 $X$ 的分布形式 $P(x)$ 已知，但是含有一个/多个未知参数 $\theta$，通过来自总体 $X$ 的一个样本来估计总体分布中未知参数值的问题。 例如假设已知总体 $X$ 的分布形式为高斯分布：$P(x) = \mathcal{N}(\mu, \sigma^2)$。 并且通过对总体 $X$ 进行一系列采样，获得 $n$ 个样本值 $x = \{x_1,...,x_n\}, x_i \in X$，如何使用 $x$ 来估计未知参数值 $\{\mu,\sigma\}$ 的问题就是点估计问题。

最大似然估计(max-likelihood estimation)法：它是点估计问题的一种求解方法。 通常而言，概率越大的样本被采样到的可能性就越大。由于我们采样到了 $x_1,..,x_n$，那么按照常理来说，这些样本所对应的概率应该较大。 最大似然估计方法就是要估计出能使采样到 $x_1,..,x_n$ 这种情况出现最大概率的参数值。 (因为这已经是既定事实，我们已经采样到了 $x_1,..,x_n$，不考虑意外情况($x_i$ 概率很小却被采样到)，通过估计能使采样到 $x_1,..,x_n$ 出现最大概率的参数值来作为预测的参数值， 是在现有观察情况下(即只观察到 $x_1,..,x_n$)能给出的最合理的参数值。 但是不一定是正确的参数值，也许我们的运气就是很背，采样到的 $x_1,..,x_n$ 在总体 $X$ 的分布中的实际概率很低， 那么此时最大似然估计所估计得到的参数值就会偏离正确的参数值很远。因此最大似然估计是一个不考虑极端采样概率发生的参数估计方法。)

具体而言，假设总体 $X$ 的分布形式 $P(X = x) = p(x;\theta), \theta \in \mathcal{\Theta}$，$X_1,...,X_n$ 是来自总体 $X$ 的一个样本， 则 $(X_1,...,X_n)$ 的联合分布律为：

根据上述分析，我们想让采样到 $x_1,..,x_n$ 这种情况出现最大概率，也就是使得上述的联合分布律最大，即：

这样，我们便求解出了估计的参数值 $\theta = \hat{\theta}$。通常而言，$\mathcal{L}(\theta) = \prod_{i=1}^np(x_i;\theta)$ 称为参数 $\theta$ 的似然函数。 $\hat{\theta}$ 称为 $\theta$ 的最大似然估计，由于其与样本值 $x_1,..,x_n$ 有关，因此也可以表示为 $\hat{\theta}(x_1,..,x_n)$。

接下来便是如何求解公式 $(2)$。由高数知识可知，当函数 $\mathcal{L}(\theta)$ 达到最大值时，其导数 $\dfrac{d}{d\theta}\mathcal{L}(\theta) = 0$， 因此我们只需要令函数 $\mathcal{L}(\theta)$ 的导数为 $0$，即可求解出满足条件的 $\theta$。 但是由于 $\mathcal{L}(\theta)$ 的表达式是乘积形式，求导比较麻烦，所以一般采用对 $ln\mathcal{L}(\theta)$ 进行求导。 一方面，$ln\mathcal{L}(\theta)$ 和 $\mathcal{L}(\theta)$ 拥有相同的单调性，即当 $ln\mathcal{L}(\theta)$ 取到最大值时，$\mathcal{L}(\theta)$ 也取到最大值。 另一方面，$ln(·)$ 函数可以将乘积形式转化为加法形式，使得求导更为简单。因此，我们便可以通过求解 $\dfrac{d}{d\theta}ln\mathcal{L}(\theta) = 0$ 来获得估计的参数值 $\hat{\theta}$。

综上所述，最大似然估计的求解步骤如下：

1. 写出似然函数：$\mathcal{L}(\theta) = \prod_{i=1}^np(x_i;\theta)$；

2. 取自然对数：$ln\mathcal{L}(\theta) = \sum_{i=1}^nln\ p(x_i;\theta)$；

3. 令 $\dfrac{d}{d\theta}ln\mathcal{L}(\theta) = 0$，即 $\dfrac{\partial ln\mathcal{L}(\theta)}{\partial\theta_i} = 0(i=1,...,m)$， 求解得到 $\hat{\theta}_i = \hat{\theta}_i(x_1,..,x_n)$。

Jensen不等式：如果 $f(x)$ 是凸函数，$X$ 是随机变量，那么：$\mathbb{E}[f(X)]\geq f(\mathbb{E}[X])$，即凸函数的期望大于等于期望的凸函数。 特别地，如果 $f(x)$ 是严格凸函数，则当且仅当 $P(X = EX) = 1$，即 $X$ 是常量时，上式取等号，即 $\mathbb{E}[f(X)]=f(\mathbb{E}[X])$。

Method

EM 算法，即期望最大化算法，其目的是求解带有隐含变量 $z$ 的最大似然值的问题。 与一般的最大似然问题不同，后者一般只包含未知分布参数 $\theta$，而前者包含未知分布参数 $\theta$ 和隐含变量 $z$。 举个例子，假设一个学校的男生和女生的身高分布都是高斯分布：$\mathcal{N}(\mu, \sigma^2)$， 其中的 $\mu_1, \sigma_1^2$ 表示男生身高分布的均值和方差；$\mu_2, \sigma_2^2$ 表示女生身高分布的均值和方差。 如果假设我们采样了 $50$ 个男生的身高分别为 $\{x_1^m,...,x_{50}^m\}$，$50$ 个女生的身高分别为 $\{x_1^w,...,x_{50}^w\}$。 在这种情况下求解对应的 $\mu_1,\sigma_1^2,\mu_2,\sigma_2^2 \rightarrow \theta$ 就是属于一般的最大似然问题。 而如果假设我们采样了 $100$ 个同学的身高分别为 $\{x_1^z,...,x_{100}^z\}$，但是并不知道每个同学的性别 $z, z\in\{m,w\}$。 此时性别变量 $z$ 就属于隐含变量，而在这种情况下求解对应的 $\mu_1,\sigma_1^2,\mu_2,\sigma_2^2 \rightarrow \theta$ 就是属于带有隐含变量 $z$ 的最大似然问题。

由于增加了未知的隐含变量 $z$，因此不能直接使用 Preliminary 中的最大似然估计法来一步到位求解参数 $\theta$。 目前已知的是总体 $X$ 的分布形式 $P(x)$ 以及 $n$ 个样本值 $x_1,...,x_n$，未知的是分布参数 $\theta$ 以及隐含变量 $z$。 如果我们可以求解出每个样本值的隐含变量 $z_i$，那么就可以将带有隐含变量 $z$ 的最大似然值的问题转化为一般的最大似然问题(例如我们求解出了采样的 $100$ 个同学的性别)。 于是，EM 算法便诞生了，其基本思想是通过迭代更新隐含变量 $z_i$ 和分布参数 $\theta$ 来实现参数求解， 即固定分布参数 $\theta$ 求解隐含变量 $z_i$，然后固定更新的 $z_i$ 求解 $\theta$，再固定更新的 $\theta$ 进一步求解 $z_i$， 通过不断的循环迭代，最终分布参数 $\theta$ 和隐含变量 $z_i$ 都将收敛到特定值。

具体而言，由 Preliminary 中的最大似然估计法可得，总体 $X$ 的似然函数为 $\mathcal{L}(\theta) = \mathcal{L}(x_1,..,x_n;\theta) = \prod_{i=1}^np(x_i;\theta)$。 在此基础上加入隐含变量 $z$ 进行进一步推导可得：

其中，不等式 $(5)$ 是由 Jensen 不等式得到的。将 $\dfrac{p(x_i,z_j;\theta)}{Q(z_j)}$ 看作一个整体 $g(z_j)$， 则等式 $(4)$ 就可以改写为：

根据上述推导，我们可以得到对数似然函数 $log\ \mathcal{L}(\theta)$ 的下界为 $\sum_{i=1}^n\sum_{z_j}Q(z_j)log\dfrac{p(x_i,z_j;\theta)}{Q(z_j)}$ (下文称为下界函数)， 根据最大似然估计法的定义，我们需要通过调整 $\theta$ 以提高对数似然函数的值(甚至直到最大值)，由于存在隐含变量无法直接求解，则可以通过不断提高下界来近似提高对数似然函数的值。 因此就将问题转化为如何求解 $z_i$ 和 $\theta$ 来提高下界函数的值(注意，这里是提高下界函数的整体值，即类似于将整个函数进行向上方向的平移。 而对数似然函数的整体值始终不变，我们只是通过提高下界函数的整体值来筛除掉 $log\ \mathcal{L}(\theta)$ 中不符合下界函数条件的 $\theta$， 即我们抛弃满足如下不等式的 $\theta: \exists z_j, log\ \mathcal{L}(\theta) < \sum_{i=1}^n\sum_{z_j}Q(z_j)log\dfrac{p(x_i,z_j;\theta)}{Q(z_j)}$)。如下图所示：

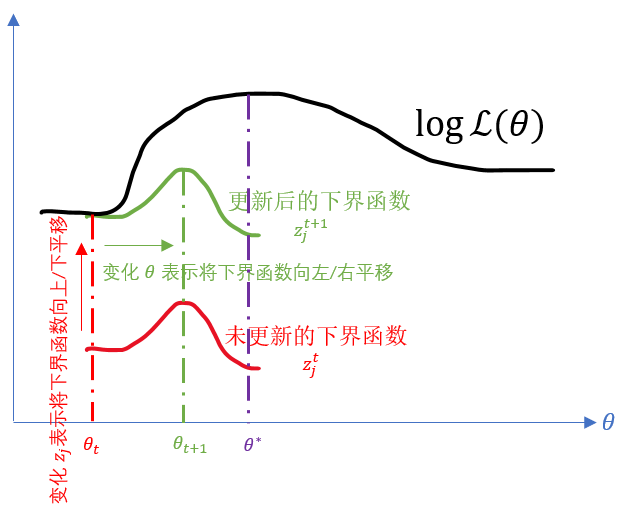
可以看到改变 $z_j$ 可以改变下界函数的整体值，我们希望下界函数越靠上越好， 但是最上只能和对数似然函数 $log\ \mathcal{L}(\theta)$ 相切(即红色线($z_j^t \rightarrow z_j^{t+1}$)，由于上述的不等式原因)； 而改变 $\theta$ 可以改变在下界函数上的取值，我们希望取到当前下界函数的越大值越好，但是最大只能到下界函数的最大值(即绿色线($\theta_t \rightarrow \theta_{t+1}$)，由于下界函数本身原因)。 因此，我们的目的就是通过求解 $z_j$ 使得下界函数和对数似然函数相切；同时求解 $\theta$ 使得取到下界函数的最大值，此时获得的 $\theta$ 即是最有可能的分布参数值，这就是 EM 算法。 具体而言，

1. 先固定 $\theta$，调整 $z_j$，使得下界函数整体值上升，即上升至与 $log\ \mathcal{L}(\theta)$ 的曲线相切处(图中红色字体)；

2. 再固定 $z_j$，调整 $\theta$，使得取到下界函数的最大值(图中绿色字体)。 此时，由于 $\theta$ 更新，下界函数的形状也发生变化(即第一步得到的 $z_j$ 已经不能满足相切条件)；

3. 然后根据新的下界函数，再重复上述 $2$ 个步骤，直到收敛到 $log\ \mathcal{L}(\theta)$ 的最大值处 $\theta^*$ (图中紫色字体)。

此时，问题进一步被转化为 1) 如何求解 $z_j$ 使得下界函数与 $log\ \mathcal{L}(\theta)$ 相切，因为 $z_j$ 和 $Q(z_j)$ 是一一对应关系，因此也可以求解 $Q(z_j)$； 2) 如何求解 $\theta$ 使得得到的参数值对应下界函数的最大值。 回顾公式 $(5)$，当下界函数与 $log\ \mathcal{L}(\theta)$ 相切时，等号成立；而在 Preliminary 的 Jensen 不等式讲解中，我们知道只有当 $X = $ (常数)时，等号才成立，即 $\dfrac{p(x_i,z_j;\theta)}{Q(z_j)} = c$。 因此：

则 $Q(z_j)$ 就是求解得到的满足下界函数与 $log\ \mathcal{L}(\theta)$ 相切的值。这便是 EM 算法的 E 步：$Q(z_j) = p(z_j|x_i;\theta)$。

而求解 $\theta$ 就相对简单，将 E 步得到的 $Q(z_j)$ 带回到 $log\ \mathcal{L}(\theta)$。然后使用一般的最大似然估计法求解即可(因为此时 $Q(z_j)$ 已经知道)：

则 $\hat{\theta}$ 就是求解得到的满足取到下界函数的最大值的参数值。这便是 EM 算法的 M 步。

总结而言，EM 算法是使用下界函数近似对数似然函数，并使用迭代求解 $Q(z_j)$ 和 $\theta$ 的方式来不断收敛。具体算法步骤如下：

1. 给分布参数 $\theta$ 赋初值 $\theta_0$；

2. E 步：固定 $\theta$ 值来计算 $Q_t(z_j)$，公式如下：

   $$Q_t(z_j) = p(z_j|x_i; \theta_t)$$

3. M 步：给定更新的 $Q_t(z_j)$ 来计算 $\theta_{t+1}$，公式如下：

   $$\theta_{t+1} = \underset{\theta \in \mathcal{\Theta}}{arg\ max}\sum_{i=1}^n\sum_{z_j}Q_t(z_j)log\dfrac{p(x_i,z_j;\theta)}{Q_t(z_j)}$$

4. 重复 $3$ 和 $4$ 步直至收敛。

Appendix

1. EM 算法收敛性证明：根据公式 $(5)$ 可得：

这里 $Q_t(z_j)$ 的下标是 $t$ 的原因是这里我们是在调整 $\theta$，固定 $Q(z_j)$，所以 $Q(z_j)$ 仍然保持上一轮的状态(即当前是 M 步)。 而 $t+1$ 轮的 $\theta_{t+1}$ 是取到下界函数的最大值所对应的 $\theta$ 值，因此：

所以就有 $log\ \mathcal{L}(\theta_{t+1}) \geq log\ \mathcal{L}(\theta_{t})$，且 $log\ \mathcal{L}(\theta)$ 有上界，因此 EM 算法可以收敛。