The Basic Knowledge of MoE
Published:
这篇博客主要讲解了使用 Mixture of Experts (MoE) 将多个模型进行组合的原理。
MoE 的基本原理
Mixture of Experts (MoE),即混合专家模型,是一种集成学习方法,旨在增加少量的计算量和内存量下,尽可能地扩大模型规模,提高模型性能。 一般来说,CNN 的模型规模和计算量/内存量呈线性关系;而 Transformer 的模型规模更是和计算量呈二次关系 (在模型宽度,即输入序列上)。 如果使用 Dense 模型(即对于每个输入数据都使用全部的参数进行计算),则会始终无法突破这种限制。 因此,MoE 模型使用 Sparse (稀疏性)的方式"绕过"该限制以实现模型性能尽可能地提升。 同时,MoE 模型也引入了在复杂预测建模问题的特定子任务上训练专家的思想, 即对于一个复杂的预测建模任务,可以将其分解为多个特定子任务,并对每个子任务训练一个模型,使得对于不同子任务的输入数据,使用不同的模型进行处理。 具体而言,MoE 模型包括 $N$ 个 expert 模型和 $1$ 个 Gating 模型:每个 expert 模型处理不同的数据分布/不同的子任务下的数据, 而 Gating 模型需要通过输入的数据 $x$,判断其属于哪个范围的数据分布/哪个子任务,并将其分配给对应的 expert 模型进行处理。 (可以简单理解为每个 expert 模型分别处理整个高维数据空间的不同子空间,而 Gating 模型需要判断输入的数据输入哪个子空间,然后送入到对应的 expert 模型进行处理。) 因此,在 Deep Learning 之前的 Machine Learning 时代,首先需要将整个数据进行划分(这一步通常根据不同的任务需求有不同的划分方式), 然后再针对划分好的数据使用 EM 算法分别训练 expert 模型和 Gating 模型。 因此如何进行数据划分便是一个主要问题。 而在 Deep Learning 时代,一般将 expert 模型和 Gating 模型都使用 Neural Network, 只需要输入数据与结果,便可使得模型自主学习数据划分、每个 expert 模型对应的数据范围以及 Gating 模型的数据划分预测。 但是,为了保证Gating 模型的数据划分预测的稀疏性,一般需要对 Gating 模型的输出进行显式限制。 同时,由于模型内部学习的不确定性,可能导致大部分数据都分配给少数的 expert 模型,需要对数据分配的平衡性进行限制。 因此,如何限制 Gating 模型输出的稀疏性、如何使用额外的方式保持 expert 模型处理数据的均衡、如何将 MoE 模型嵌入已有模型框架以及更好地融入现有硬件框架进行训练等, 都是目前需要考虑和改进的问题。
MoE 在 Deep Learning 的应用
目前 MoE 模型主要与 LLM 和 Transformers 进行结合。具体而言,Transformers 中包含 Self-Attention、Cross-Attention 和 FFN $3$ 个子模块。 以 Encoder 为例,假设 $1$ 个 Transformers Encoder 共有 $L$ 层,通过将每层/隔层的 $\text{FFN}^l$ 模块扩展为 $N$ 个 ($\text{FFN}_1^l \sim \text{FFN}_N^l, l = 1,...,L$) 组成 $N$ 个 expert 模型, 并为每层/隔层训练 $1$ 个独立的 Gating 模型 $G^l(·), l=1,...,L$。则每层的输出为: $$\bar{I}^l = \operatorname{LayerNorm}(\operatorname{Self-Attn}(I^l) + I^l); \\ O^l = \operatorname{LayerNorm}(\sum_{i=1}^NG^l_i(\bar{I}^l)\operatorname{FFN}^l_i(\bar{I}^l) + \bar{I}^l)$$可以看到, 每个 expert 模型的架构基本和 FFN 一致,因此后续工作基本集中在 Gating 模型的设计和总体模型的训练上。 其中主要包括如何设计 Gating 模型;如何减轻负载不均衡问题以及如何训练 MoE 模型等
名词解释:
expert capacity:每个 expert 模型在每次 batch 中所能处理的最大数据量。 假设一共有 $N$ 个 expert 模型,$1$ 个 batch $\mathcal{B}$ 的数据量为 $T$, 理想情况下,应该由 $N$ 个 expert 模型平均处理,即每个 expert 模型处理 $\dfrac{T}{N}$ 个数据。但是由于 Gating 模型分配的不确定性,可能会导致部分 expert 模型需要处理的数据量 $> \dfrac{T}{N}$;而部分 expert 模型需要处理的数据量 $< \dfrac{T}{N}$。 极端情况下,Gating 模型可能会将所有 $T$ 个数据都分配给 $1$ 个 expert 模型,这会导致计算内存超过 expert 模型所在的 GPU 块/集群(即 OOM)。 因此,需要对每个 expert 模型设置所能处理的最大数据量,通常为均值 $\dfrac{T}{N}$ 再乘上 $1$ 个容量因子 $c$: $$EC = \text{expert capacity} = (\dfrac{\text{tokens per batch}}{\text{number of experts}}) \times \text{capacity factor} = \dfrac{T}{N} \times c$$ 其中容量因子 $c$ 表示缩放程度,对于不同的任务具有不同的值。此时,当 Gating 模型分配的数据量 $> EC$ 时,expert 模型只会处理前 $EC$ 个, 而其余的数据会通过 Transformer 的残差连接直接进入下一层(即该层的处理视为恒等映射);当 Gating 模型分配的数据量 $< EC$ 时, 则会将剩余的空白位置赋值为 $0$ (以方便批量化处理)。
Gated Linear Unit:GLU 是一个用于建模序列关系的标准模块。与 MLP 和 $Attention$ 不同,它通过将序列数据映射为 $2$ 个不同的特征并进行融合来实现序列之间的关系建模。 具体而言,假设序列数据为 $\mathbf{X} \in \mathbb{R}^{N \times m}$,则 GLU 的数学表达式为: $$\mathbf{X}'=(\mathbf{X}*\mathbf{W}+\mathbf{b})\otimes\sigma(\mathbf{X}*\mathbf{V}+\mathbf{c})$$ 其中 $\mathbf{W} \in \mathbb{R}^{k \times m \times n}$ 和 $\mathbf{V} \in \mathbb{R}^{k \times m \times n}$ 表示线性权重; $\mathbf{b} \in \mathbb{R}^{n}$ 和 $\mathbf{c} \in \mathbb{R}^{n}$ 表示线性偏差($m,n$ 表示输入/输出维度,$N$ 表示序列数据长度,$k$ 表示 patch size); $\sigma(\cdot)$ 表示激活函数。
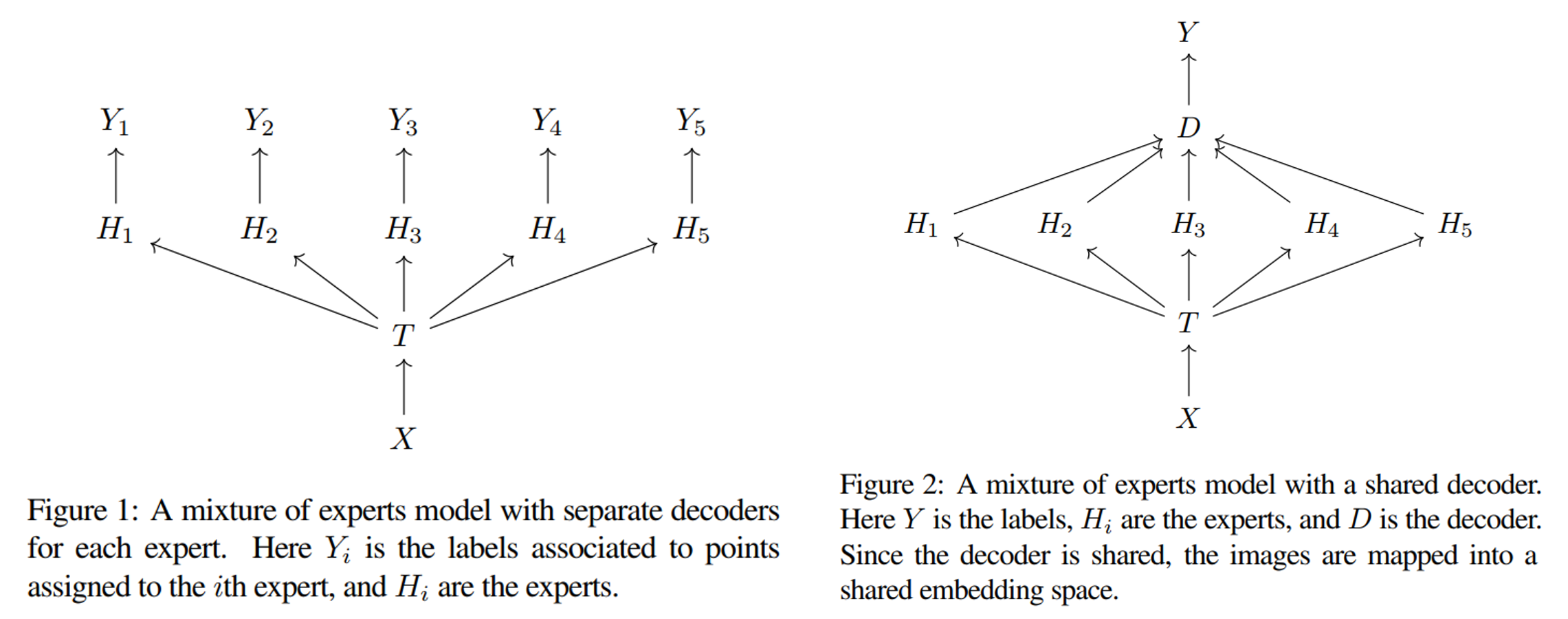
K-means:该方法使用 k-means 聚类的方法来实现 Gating Model。 它将每个 expert 模型所映射的特征空间视为 $1$ 个簇,则 $N$ 个 expert 模型分别表示 $N$ 个簇。 接着通过计算新数据 $x$ 的特征值到各个簇之间的最小距离,即可确定该数据应该由哪个 expert 模型进行处理。 同时,它使用分离式训练方式,先训练 Gating Model,在使用训练完成的 Gating Model 训练 $N$ 个 expert 模型。 具体而言,假设有数据集 $\mathcal{D} = \{x_i, y_i\}_N$。首先使用数据集 $\mathcal{D}$ 训练 $1$ 个 $L$ 层的分类器模型 $T$ (即 Gating Model)。 然后将其最后一层(即 $L-1$ 层)的输出值 $z_i = T^{L-1}(x_i)$ 作为数据 $x_i$ 的特征值, 则对于数据集 $\mathcal{D}$ 中的每个数据 $x_j$ 都能生成一个对应的特征值 $z_j$,组成特征集 $\mathcal{F} = \{x_j, z_j\}_N$。 接着针对特征集 $\mathcal{F}$ 进行 k-means 聚类,聚类个数为 $K$,则最终会获得 $K$ 个聚类中心 $c_1,...c_K$。 这些聚类中心即可视为不同的数据分布,需要不同的 expert 模型进行学习处理,即 $1$ 个聚类中心表示一个 expert 模型。 因此需要 $K$ 个 expert 模型,分别为 $H_1(x) \sim H_K(x)$。 接着对于训练集中的每个数据 $x$,计算其到各个聚类中心 $c_j$ 的距离,并选择最短距离的聚类中心 $c_i$ 所对应的 expert 模型 $H_{i}(x)$ 作为处理 $x$ 的模型。 在具体实现上,可以使用二值函数来实现对每个 expert 模型的选择,即: $$T(x)_i= \begin{cases}1, & \text { if } i=\operatorname{argmin}_j\left\|T^{L-1}(x)-c_j\right\|_2 \\ 0, & \text { otherwise }\end{cases} \\ O = \sum_{j=1}^KT(x)_jH_j(x) = T(x)_iH_i(x)$$ 由于对于每个数据 $x$,$T(x)$ 仅有第 $i$ 个位置为 $1$,其余位置均为 $0$,再使用加权求和方式进行计算,即可表示选择第 $i$ 个 expert 模型 $H_{i}(x)$。 由于显式使用 k-means 进行分类,保证每个 expert 模型 $H_i(·)$ 都只训练特定的数据,与 MoE 最原始的目的相一致。 而在训练完成后,对于一个新数据 $\bar{x}$,首先通过分类器模型 $T$ 输出其特征值:$\bar{z} = T^{L-1}(\bar{x})$。 然后使用公式 $(1)$ 计算需要使用的 expert 模型 $H_{i}(\bar{x})$,并最终获得输出 $\bar{O}$。 而有些时候,可能需要的不是最终的预测输出,而是模型所学习的特征(即一般取模型的最后一层的输出值),而 $N$ 个 expert 模型含有 $N$ 个不同的特征值。 一种方式是直接选择 $T(x)$ 为 1 的位置所对应的 expert 模型的特征值; 另一种方式是在 $N$ 个 expert 模型之后再学习一个共享的解码器 Decoder,然后以解码器的最后一层输出值为特征值: $$T(x)_i= \begin{cases}1, & \text { if } i=\operatorname{argmin}_j\left\|T^{L-1}(x)-c_j\right\|_2 \\ 0, & \text { otherwise }\end{cases} \\ O = \text{Decoder}(\sum_{j=1}^KT(x)_jH_j(x)) = \text{Decoder}(T(x)_iH_i(x))$$
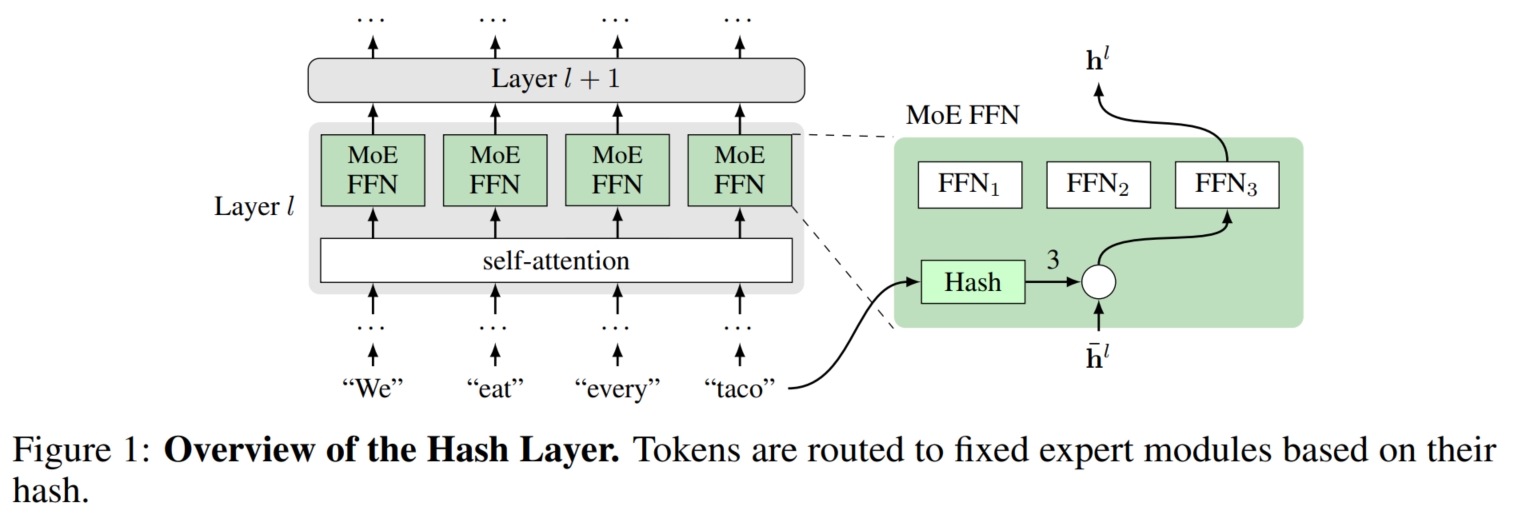
Hash:该方法使用 hash 的方法来实现 Gating Model。 它使用预定义的 hash 函数,将输入数据 $x$ 映射为 $1 \sim N$ 之间的数字 $i$,表示 $x$ 由第 $i$ 个 expert 模型处理。 具体而言,假设有 $K$ 个 expert 模型,分别为 $H_1(x) \sim H_K(x)$。对于输入数据 $x$,首先使用给定的 hash 函数将其映射为数字 $i$, 然后使用第 $i$ 个 expert 模型 $H_i(x)$ 处理数据 $x$,最终得到输出 $O$: $$O = H_{hash(x)}(x); hash(x) \sim [1, K]$$在 Transformer 架构中,第 $l$ 层中的每个 expert 模型以前 $1$ 层(即第 $l-1$ 层)的输出 $O^{l-1}$ 为输入; 而每一层的 hash 函数都以原始输入 $x$ 为输入。可以看到,对于输入数据 $x$,其 hash 值固定,因此每一层的 MoE 模型所选择的 expert 模型也是固定的(即每一层都选择第 $hash(x)$ 个模型)。 同时,还可以利用多个 hash 函数来降低模型对于单个 hash 函数的依赖。 具体而言,假设有 $N$ 个不同的 hash 函数, FFN 模块由 $2$ 层线性层 $A:\mathbb{R}^d \rightarrow \mathbb{R}^D; B:\mathbb{R}^D \rightarrow \mathbb{R}^d$ $+$ $\operatorname{ReLU}$。 对于第 $l$ 层,首先将 $A, B$ 线性层划分为 $N$ 份:$A_m^l:\mathbb{R}^d \rightarrow \mathbb{R}^{D/N}; B_m^l:\mathbb{R}^D \rightarrow \mathbb{R}^{d/N}$; 然后每个 hash 函数分别将输入数据 $x$ 映射为不同的值:$k_m = hash_m(x), m=1,...,N$; 最后使用 $A_{k_1}^l,...,A_{k_m}^l$ 与 $B_{k_1}^l,...,B_{k_m}^l$ 分别计算: $$v^l=\operatorname{ReLU}\left(\left[A_{k_1}(I^l), \ldots, A_{k_N}(I^l)\right]\right) \quad \operatorname{FFN}(I^l)=\left[B_{k_1}(v^l), \ldots, B_{k_N}(v^l)\right] \\ O^l = \operatorname{FFN}_{hash(x)}(I^l)$$
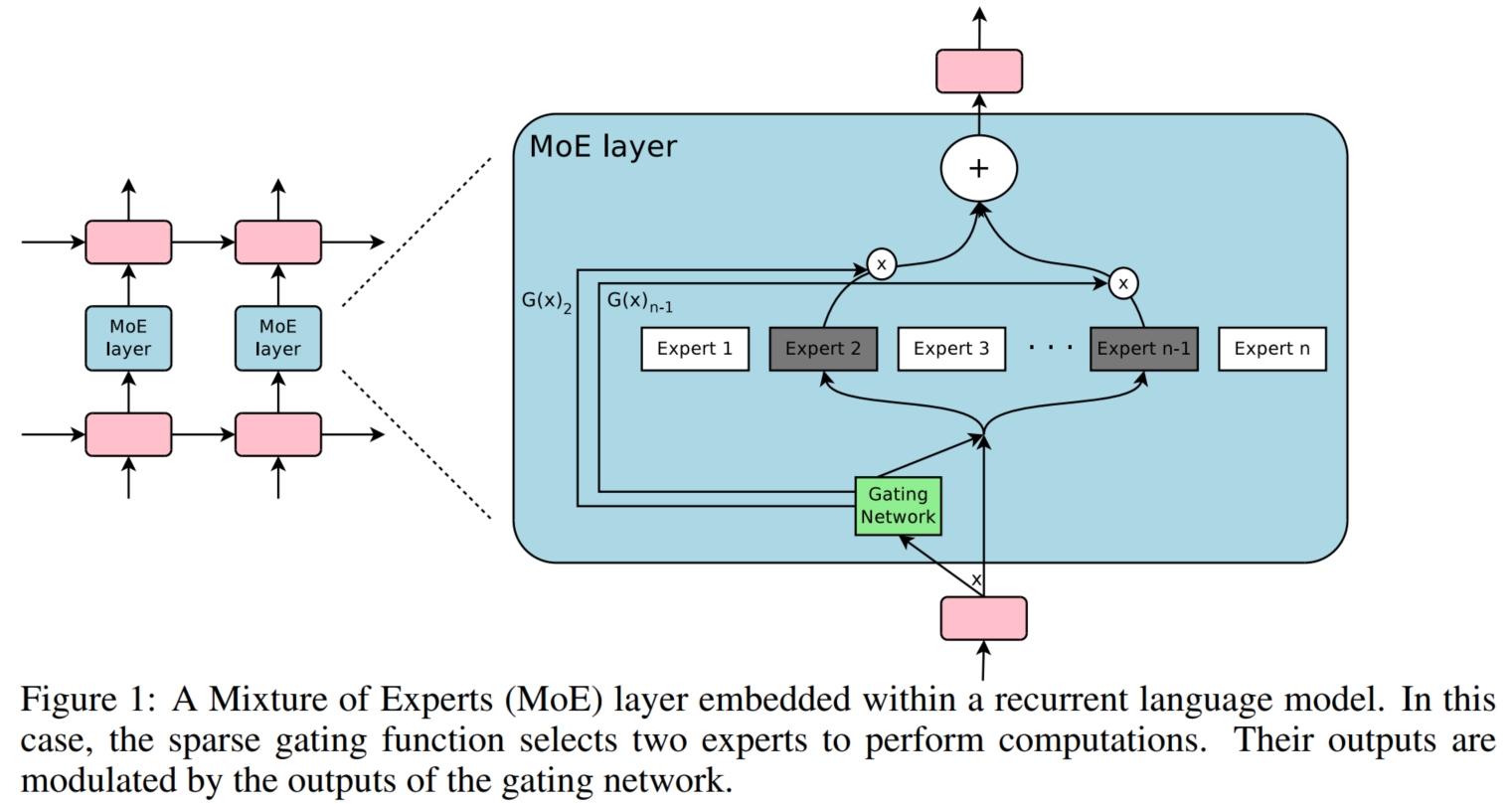
Sparsely-Gated: 假设有 $K$ 个 expert 模型,分别为 $H_1(x) \sim H_K(x)$。 对于输入数据 $x$,最简单的 Gating Model 是使用线性权重 $W_g$ 将数据 $x$ 映射为 $K \times 1$ 的维度,然后使用 $Softmax$ 函数将其转化为 expert 模型的权重, 最后对所有 expert 模型的输出进行加权求和: $$O = \sum_{i=1}^KG(x)_iH_i(x); G(x) = softmax(x \times W_g)$$这种方法有一个问题,MoE 无法学习到精确的稀疏权重, 使得对于每个输入数据基本上都需要使用全部的 $K$ 个 expert 模型进行计算。这与 MoE 的原始目的相违背。 因此,需要显式地引入稀疏限制。具体而言,首先,对于 Gating Model,为了使其产生的权重稀疏,需要在 softmax 函数之前进行值限制: 只保留 $x \times W_g$ 前 $k$ 个值(从大到小),将其余值设为 $-\infty$,则在经过 softmax 函数后,仅有前 $k$ 个值所对应的权重 $\neq 0$,而其余值所对应的权重均为 $0$。 此时,对于那些为 $0$ 的权重,就不需要计算其对应的 expert 模型的输出值。因此,只需对前 $k$ 个的 expert 模型进行加权求和即可: $$O = \sum_{i=1}^KG(x)_iH_i(x); G(x) = softmax(KeepTopK(x \times W_g, k)) \\ \text { KeepTopK }(v, k)_i= \begin{cases}v_i & \text { if } v_i \text { is in the top } k \text { elements of } v \\ -\infty & \text { otherwise. }\end{cases}$$ 此外,还通过向 $x \times W_g$ 中加入一定程度的噪声来促进 Gating 模型对不同数据的均匀分配(即均匀分配给各个 expert 模型),其中噪声程度由参数 $W_{\text{noise}}$ 控制: $$G(x)=\operatorname{Softmax}(\operatorname{KeepTopK}(H(x), k)) \\ H(x)_i=\left(x \cdot W_g\right)_i+\operatorname{StandardNormal}() \cdot \operatorname{Softplus}\left(\left(x \cdot W_{\text {noise }}\right)_i\right)$$ 为了减轻负载不均衡问题(即 Gating 模型将大多数数据都分配给少数 expert 模型),需要引入额外的损失函数。 由于直接统计各个 expert 模型所处理的数据数是无法求导的,因此需要使用其他的近似策略进行代替。 第一种方法是权重均衡限制:该方法遵循一种假设:对于一个 batch 中的数据,如果各个 expert 模型对于所有数据的 Gating 权重之和相近, 则说明 expert 模型之间负载均衡。因此首先定义 expert 模型的重要性为其关于一个 batch 中的所有数据的 Gating 权重之和: $$\operatorname{Importance}(X)=\sum_{x \in X} G(x); X \text{ is A Batch}$$ 然后定义重要性损失等于所有 expert 模型的重要性值 $\operatorname{Importance}$ 的变异系数的平方,乘以缩放因子 $w_{\text{importance}}$: $$L_{\text {importance }}(X)=w_{\text {importance }} \cdot C V(\operatorname{Importance}(X))^2$$ 第二种方法是光滑估计限制:权重均衡限制的一种极端情况是几个 expert 模型可能处理几个大 Gating 权重的数据, 而另外几个专家可能会处理很多小 Gating 权重的数据,从而依旧导致负载不均衡。 因此,此方法定义 $1$ 个光滑估计器 $\operatorname{Load}(x)$ 近似表示 $1$ 个 batch 中分配给每个 expert 模型的数据数。 首先定义 $P(x;i)$ 作为 $G(x)_i \neq 0$ 的概率(这个概率是通过给定元素 $i$ 上的一个新的随机噪声选择(但保持其他元素上已经采样的噪声选择)来进行变化的, 即 $\operatorname{StandardNormal}()$),即当且仅当 $H(x)_i > H(x)$ 中不包含第 $i$ 个元素(即自己)的第 $k$ 大元素时的概率: $$\begin{align}P(x, i) & =\operatorname{Pr}\left(\left(x \cdot W_g\right)_i+\text { StandardNormal }() \cdot \operatorname{Softplus}\left(\left(x \cdot W_{\text {noise }}\right)_i\right) > \operatorname{kth\_excluding}(H(x), k, i)\right) \\ & = \Phi\left(\dfrac{(x \cdot W_g)_i - \text { kth_excluding }(H(x), k, i))}{\operatorname{Softplus}\left(\left(x \cdot W_{\text {noise }}\right)_i\right)}\right)\end{align}$$ 其中,$\operatorname{kth\_excluding}(v;k;i)$ 表示 $v$ 的第 $k$ 个最高分量,不包括分量 $i$;$\Phi$ 表示标准正态分布的累积分布函数。 因此,光滑估计器 $\operatorname{Load}(x)$ 为:$\operatorname{Load}(x)_i = \sum_{x \in X}P(x,i)$; 则负载损失函数就定义为光滑估计器 $\operatorname{Load}(x)$ 的变化系数的平方,乘以缩放因子 $w_{\text{load}}$: $$L_{\text {Load }}(X)=w_{\text {load }} \cdot C V(\operatorname{Load}(X))^2$$ 此外,MoE 模型会引入 shrinking batch 问题:假设正常情况下一个 batch 的数据量为 $b$,一共有 $n$ 个 expert 模型,且每个数据都选择 $k$ 个 expert 模型, 则每个 expert 模型实际分到的数据量为 $\frac{kb}{n} \ll b$ (因为 $k \ll n$)。 为此可以将 Data Parallelism 和 Model Parallelism 进行结合以提高每个 expert 模型分配的数据量。 具体而言,假设有 $N$ 个 GPU 块/集群,每个 GPU 块都能独立运行 $1$ 个非 MoE 模型下的普通模型, 则对于 MoE 模型,将其中的非 MoE 模块(如 $\text{Self-Attn、Cross-Attn}$)复制 $N$ 次分布在各个 GPU 块上(即 Data Parallelism), 而对于 MoE 模块(如 $\text{FFN}$),将其 $n$ 个 expert 模型分布在各个 GPU 块上(即 Model Parallelism。 因此,每个 GPU 块上包含相同参数的非 MoE 模块 和不同的 expert 模型)。则此时每次训练的 $1$ 个 batch 的数据量为 $Nb$, 而分配到每个 expert 模型的数据量为 $\frac{kbN}{n}$。
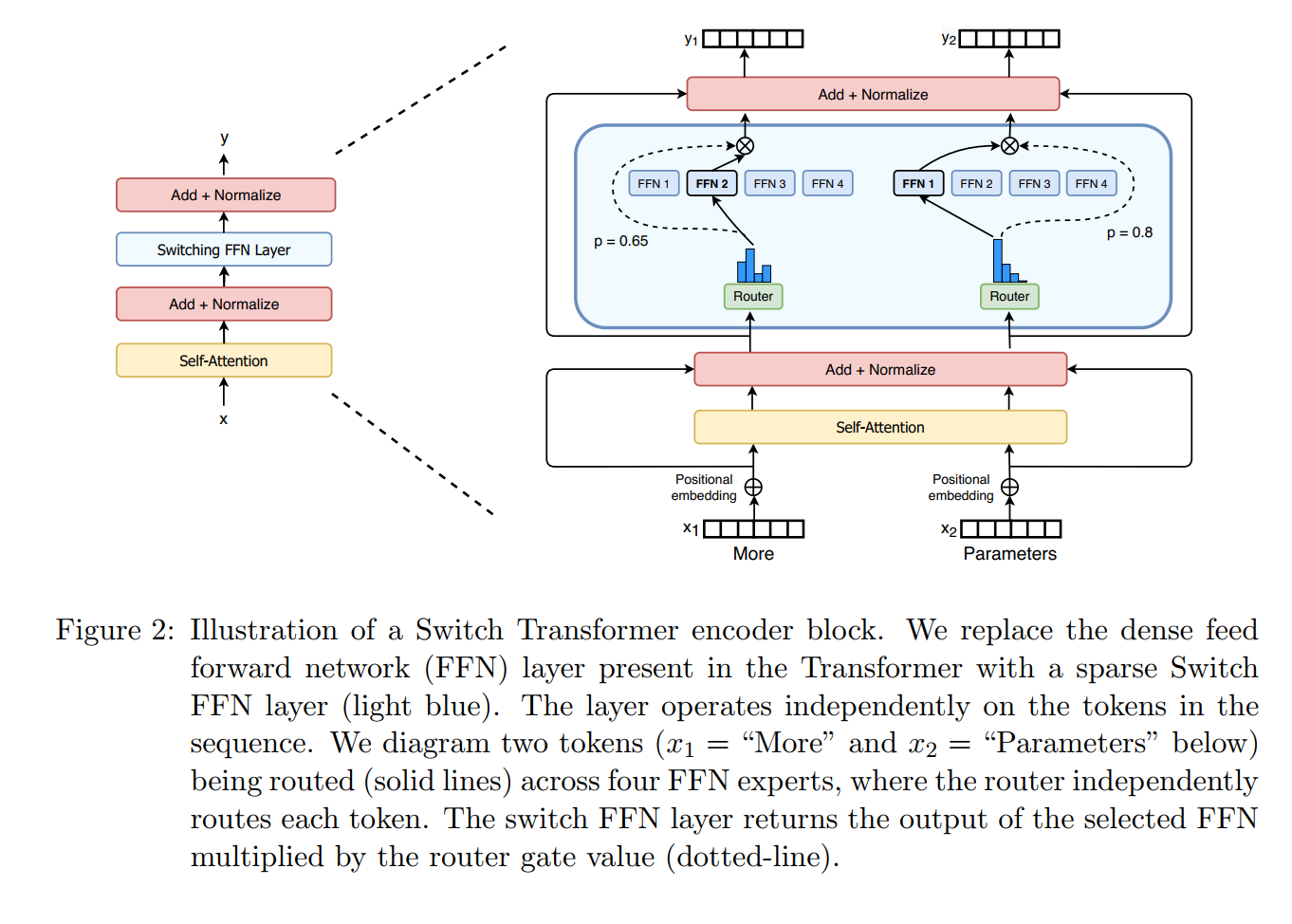
Switch Transformers: 它对 MoE 模型的 Gating Model 进一步进行简化,使得对于每个数据 $x$,只会有 $1$ 个 expert 模型进行处理。 具体而言,它将上述的 Sparsely-Gated 模型中的 $topk$ 值设为 $1$,即只取 $x \times W_g$ 中的最大值,将其余值设为 $-\infty$: $$O = \sum_{i=1}^KG(x)_iH_i(x); G(x) = softmax(KeepTopK(x \times W_g, 1)) \\ \text { KeepTopK }(v, k)_i= \begin{cases}v_i & \text { if } v_i \text { is in the top } k \text { elements of } v \\ -\infty & \text { otherwise. }\end{cases}$$ 为了减轻负载不均衡问题,Switch transformers 引入负载均衡损失函数,其将 Sparsely-Gated 中的重要性损失和负载损失函数的结合与简化。 具体而言,假设有 $N$ 个 expert 模型,且 $1$ 个 batch $\mathcal{B}$ 中的数据量为 $T$。 首先,定义 $f_i$ 为 $\mathcal{B}$ 中分配给第 $i$ 个 expert 模型的数据比例: $$f_i = \dfrac{1}{T}\sum_{x\in\mathcal{B}}\mathbb{1}\{argmax\ G(x) = i\}$$ 其次定义 $P_i$ 为 $\mathcal{B}$ 中所有数据的第 $i$ 个 expert 模型的 Gating 值之和: $$P_i = \dfrac{1}{T}\sum_{x\in\mathcal{B}}G(x)_i$$ 最后,定义负载均衡损失函数为 $f$ 和 $P$ 的点积之和: $$loss = \alpha \cdot N \cdot \sum_{i=1}^{N}f_i \cdot P_i$$ 其中,$\alpha$ 为乘积因子;而 $\times N$ 是为了使损失与 expert 模型的数量无关 (因为 $\sum_{i=1}^N(f_i \cdot P_i) \propto \sum_{i=1}^N(\dfrac{1}{N} \cdot \dfrac{1}{N} = \dfrac{1}{N})$)。 同时,为了减轻模型训练的不稳定性,Switch transformers 引入多个改进方法: 1. 选择性提高计算精度:在混合精度算法中, 模型的前向计算过程均为 $bfloat16$ 的计算精度,这会导致 MoE 模型训练的不稳定;而全部使用 $float32$ 的计算精度又会导致计算和通信复杂度的提高。 因此,可以通过将局部模型的计算精度提高来减轻训练不稳定性,同时又不过多增加计算和通信复杂度。 具体而言,将 Gating 模型的输入转换为 $float32$ 精度。 Gating 模型将数据 $x$ 作为输入,并生成用于选择和重组 expert 模型的分派和组合张量 $G(x)_i$(即各个权重)。 重要的是,$float32$ 精度只在 Gating 模型的计算中使用,即只用于每个 GPU 块的本地计算。 由于最终的分发和合并张量 $G(x)_i$ 在模型输出后被重新转换为 $bfloat16$ 精度, 因此通过 all-to-all 通信操作广播的依旧是 $bfloat16$ 张量,即通信复杂度不会增加。 2. 更小的模型参数初始化:一般模型参数都是通过从截断的正态分布中随机生成来初始化权重矩阵,其中均值 $\mu = 0$,标准差 $\sigma = \sqrt{s/n}$。 其中 $s$ 是尺度超参数,$n$ 是参数权重中输入单元的数量(即输入的长度)。通过降低 $s$ (如 $10 \rightarrow 1$),可以提高模型训练的稳定性。 3. expert 模型内部更高正则化:在 MoE 模型微调过程中,在每个 expert 模型的计算时(即 FFN), 将 drop-out 率(称为 expert dropout)显著增加(如 $0.1 \rightarrow 0.4$);而保持其他非 MoE 模块的 drop-out 率不变,可以提高模型性能。
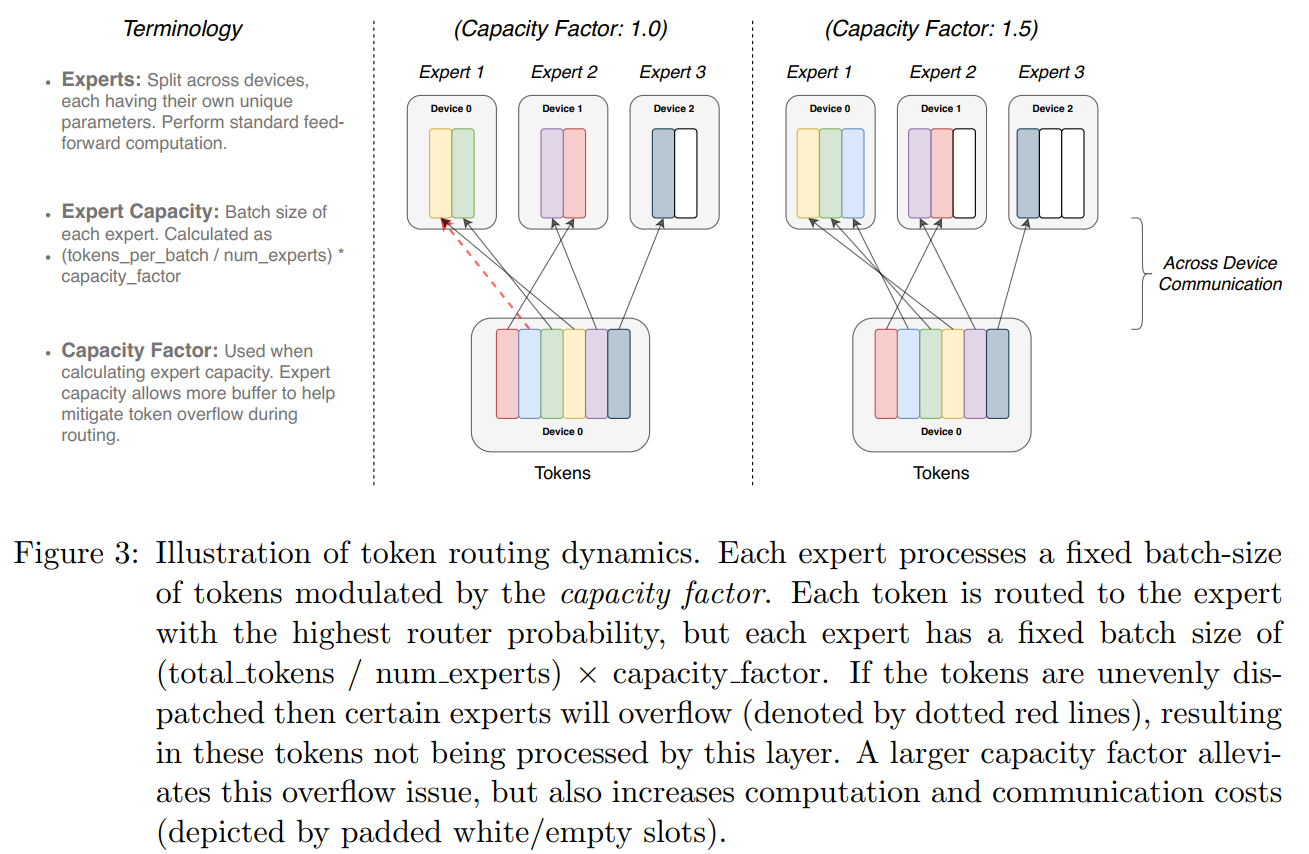
GLaM: 它与 Switch Transformers 相似,都是对 MoE 模型的 Gating Model 进一步进行简化。它使得对于每个数据 $x$,只会有 $2$ 个 expert 模型进行处理。 具体而言,它将上述的 Sparsely-Gated 模型中的 $topk$ 值设为 $2$,即只取 $x \times W_g$ 中前 $2$ 个值(从大到小),将其余值设为 $-\infty$: $$O = \sum_{i=1}^KG(x)_iH_i(x); G(x) = softmax(KeepTopK(x \times W_g, 2)) \\ \text { KeepTopK }(v, k)_i= \begin{cases}v_i & \text { if } v_i \text { is in the top } k \text { elements of } v \\ -\infty & \text { otherwise. }\end{cases}$$ 与之前的方法不同的是,它没有将 Transformer 中每层的 FFN 模块都替换为 MoE 模块; 而是使用隔层替换,即 $1$ 层为原始的 Transformer 块($\text{Self-Attn} + \text{FFN}$),$1$ 层为 MoE 块($\text{Self-Attn} + \text{FFN}_{\text{MoE}}$)。 此外,它将传统的绝对位置编码(即 $sin/cos$ 编码)替换为逐层的相对位置编码; 将原始的 Transformer 块中的 $\text{FFN}$ 模块的第一层线性映射 $+$ 激活函数替换为 $GLU (\text{Gated Linear Unit}) + \text{Gaussian Error Linear Unit}$。

GShard: 它与 GLaM 相似,都是对 MoE 模型的 Gating Model 进一步进行简化。 它通过利用 Gating Model 的输出值动态调整,使得对于每个数据 $x$,最多仅有 $2$ 个 expert 模型进行处理。 具体而言,它将上述的 Sparsely-Gated 模型中的 $topk$ 值设为 $2$,即只取 $x \times W_g$ 中前 $2$ 个值 $g_1$ 和 $g_2$ (从大到小),将其余值设为 $0$。 接着将 $g_1, g_2$ 进行归一化,然后将 $g_1$ 所对应的 expert 模型 $e_1$ 对数据 $x$ 进行处理。 同时判断 $g_2$ 是否大于阈值 $T$:如果大于,则将 $g_2$ 所对应的 expert 模型 $e_2$ 对数据 $x$ 进行处理;反之,则丢弃 $g_2$,即设为 $0$: $$g = softmax(W_g \times x); g_1, g_2 = KeepTopK(g, 2) \\ \text { KeepTopK }(v, k)_i= \begin{cases}v_i & \text { if } v_i \text { is in the top } k \text { elements of } v \\ -\infty & \text { otherwise. }\end{cases} \\ g_1 = g_1/(g_1 + g_2); g_2 = g_2/(g_1 + g_2); g_2 = \begin{cases} g_2 \text { if } g_2 \geq T \\ 0 \text { otherwise. }\end{cases}; T \sim U(0, 1) \\ O = \sum_{i=1}^Kg_iH_i(x)$$ 为了尽可能保证各个 expert 模型负载平衡,它使用 Local Group Dispatching:将 $1$ 个 batch $\mathcal{B}$ 的数据(数据量为 $N$)平均分成 $G$ 份(则每份为 $S = \dfrac{N}{G}$)。 针对每个数据组,也将每个 expert 模型的 expert capacity 进行平均划分,即对于每个数据组,为每个 expert 模型分配 $\dfrac{2N}{G\cdot E}$ 的 expert capacity。 同时使用附加损失函数(Auxiliary loss)进一步平衡每个 expert 模型的负载: $$\mathcal{L}_{aux} = \dfrac{1}{S}\sum_{e=1}^{K}{\frac{c_e}{S}\cdot m_e} \\ c_e\ \text{是第 e 个 expert 模型所分配到的数据量}; \\ m_e = \dfrac{1}{S} g_{s,e}\ (\text{是 Gating 模型分配给所有数据针对第 e 个 expert 模型的权重之和})$$ 正常情况下,为了平衡每个 expert 模型的负载,应该将辅助损失函数设计为 $(\frac{c_e}{S})^2$,但是由于 $c_e$ 的不可导限制, 因此将其中 $1$ 个 $c_e$ 替换为可导的 $m_e$ 进行近似。
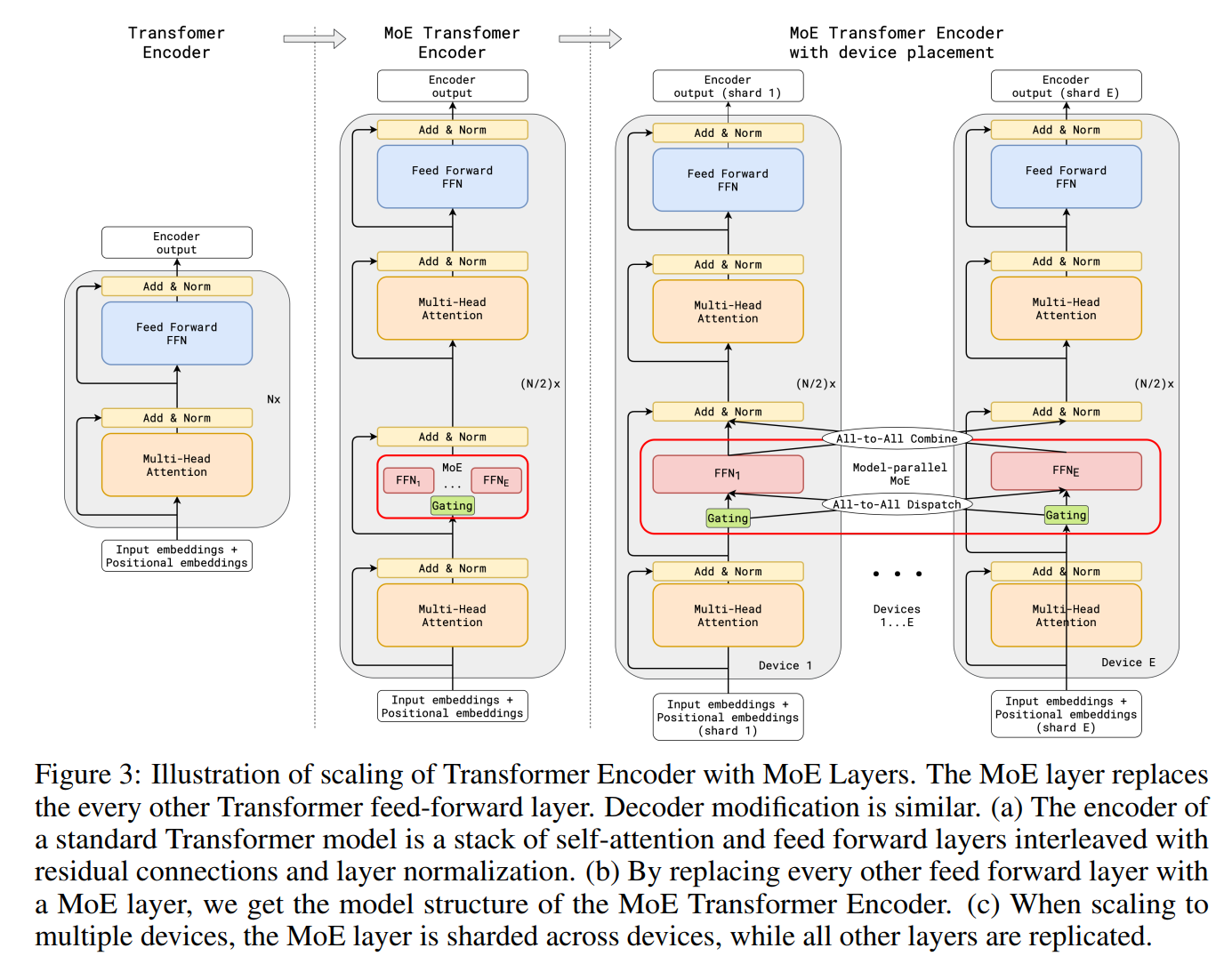

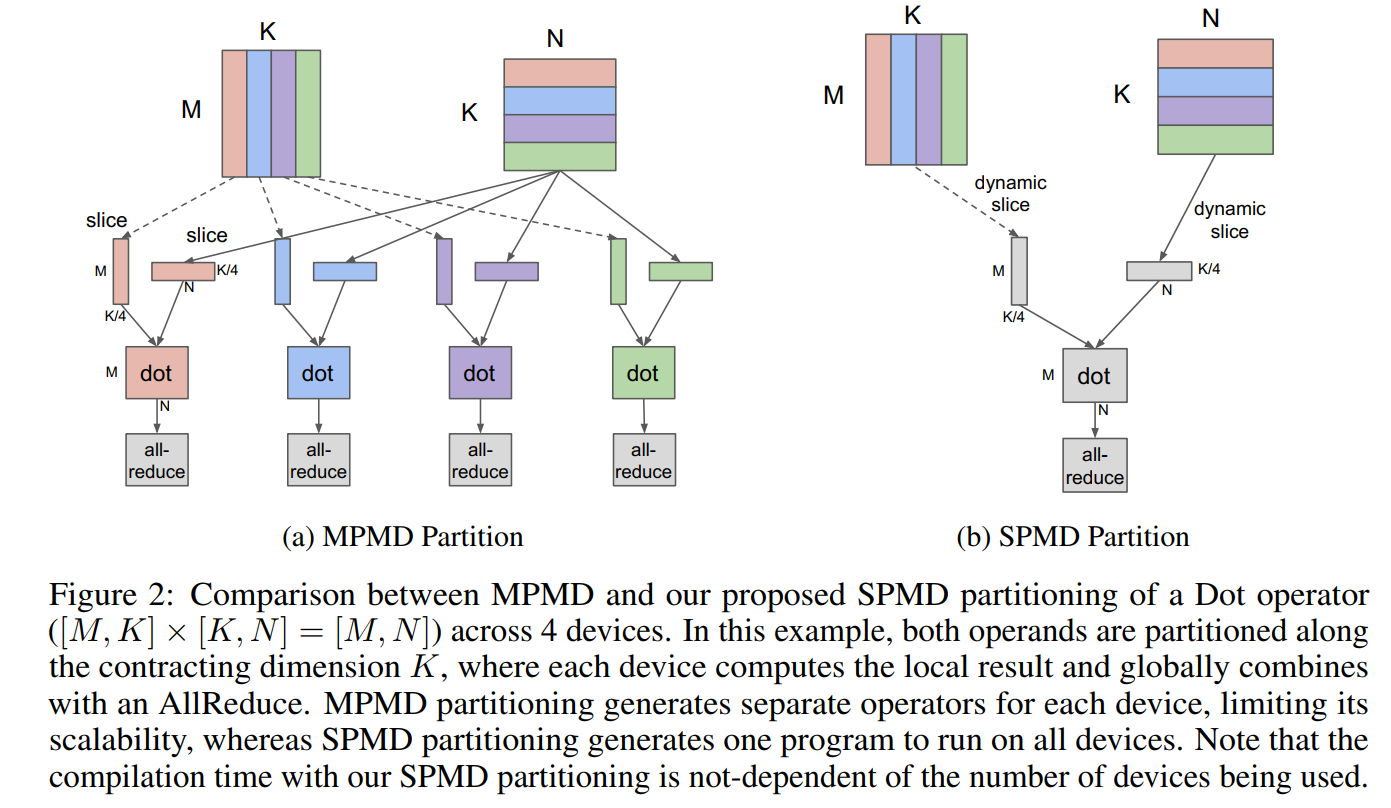
V-MoE: 它将 Sparsely-Gated 应用到 Vision 领域,并对 Gating Model 进一步进行改进。 具体而言,将 $\text{ KeepTopK }$ 函数应用于 $\text{ Softmax }$ 函数之后,同时引入正态分布噪声 $\epsilon$ 增强训练稳定性: $$g(\mathbf{x})=\operatorname{KeepTopK}(\operatorname{softmax}(\mathbf{W} \mathbf{x}+\epsilon), k); \epsilon \sim \mathcal{N}(0, \frac{1}{E^2})\\ O = \sum_{i=1}^kg_iH_i(x)$$ 其中,假设 $1$ 个 batch 中的图片数量为 $N$,每个图片的 patch 数量为 $P$,每个 token (patch) 所选择的 expert 模型数量为 $k$, expert 模型的数量为 $E$,expert capacity 的松弛因子为 $C$,则每个 expert 模型的 expert capacity 为 $B_e = \operatorname{round}\big(\dfrac{kNPC}{E}\big)$。 对于图片而言,并不是每个 patch 的重要性都相同,很多时候只需要注意前景物体,而背景忽视即可。 因此,对于一张图片,需要提高重要 patch 的优先级(即优先给 expert 模型处理),而对于不重要的 patch,可以设置 $C \ll 1$ 使得 expert 模型忽略它, 从而达到节省计算量的目的。具体而言,V-MoE 提出了 Batch Prioritized Routing (BPR) 的 expert 模型分配算法: 假设 $1$ 个 batch 的数据量维度为 $X \in \mathbb{R}^{N \cdot P \times D}$, 则 Gatind 模型的输出维度为 $g(X) \in \mathbb{R}^{N \cdot P \times E}$,其中 $g(X)_{t,i}$ 表示第 $t$ 个 token 选择第 $i$ 个 expert 模型的概率。 V-MoE 定义一个优先级分数(priority score) $s(X)$,其中 $s(X)_t = max_i(g(X)_{t,i}) \text{or} \sum_{i=1}g(X)_{t,i}$。 然后按照 $s(X)$ 的从大到小的优先级顺序依次选择每个 token (patch) 所处理的 $k$ 个 expert 模型。 同时为了平衡每个 expert 模型的负载,V-MoE 借鉴了 Sparsely-Gated 的 $2$ 个辅助损失函数,并对其进行细微修改。 具体而言,对于重要性损失,其选择特定层的 MoE 模型的 Gating 模型的结果权重进行计算: $$\text{Imp}_i(X) = \sum_{x\in X}\operatorname{softmax}(Wx)_i \rightarrow \text{Imp}(X):=\{\text{Imp}_i(X)\}_{i=1}^E\\ \mathcal{L}_{\mathrm{Imp}}(\mathbf{X})=\left(\frac{\mathrm{std}(\mathrm{Imp}(\mathbf{X}))}{\mathrm{mean}(\mathrm{Imp}(\mathbf{X}))}\right)^2\propto\mathrm{var}(\mathrm{Imp}(\mathbf{X})).$$ 其中,$W$ 表示 Gating 模型的权重 $\mathbf{W}$ 中的一些特定层的部分权重。而对于负载损失,V-MoE 将 $\operatorname{kth\_excluding}(v;k;i)$ 函数简化为阈值: $$\mathrm{th}\text{reshold}_k(\mathbf{x}):=\max_{k\text{-th}} \left ( W \mathbf{x}+\epsilon\right)$$ 然后计算第 $i$ 个 expert 模型在数据 $x$ 的前 $k$ 个的候选模型的概率: $$p_i(\mathbf{x}):=\mathbf{P}((W\mathbf{x})_i+\epsilon_\text{new}\geq\text{threshold}_k(\mathbf{x}))=\mathbf{P}(\epsilon_\text{new}\geq\text{threshold}_k(\mathbf{x})-(W\mathbf{x})_i)\\ \epsilon_{\text{new}}\sim\mathcal{N}(0,\sigma^2)\text{, with }\sigma=1/E$$ 则第 $i$ 个模型关于 batch $\mathcal{B}$ (其中数据为 $X$)的负载分布可定义为: $$\mathrm{load}_i(\mathbf{X})=\sum_{\mathbf{x}\epsilon\mathbf{X}}p_i(\mathbf{x})$$ 最后,负载损失函数正比于负载分布变化的平方系数: $$\mathcal{L}_{\mathrm{load}}(\mathbf{X})=\left(\frac{\mathrm{std}(\mathrm{load}(\mathbf{X}))}{\mathrm{mean}(\mathrm{load}(\mathbf{X}))}\right)^2,\quad\mathrm{load}(\mathbf{X}):=\{\mathrm{load}_i(\mathbf{X})\}_{i=1}^E.$$ 因此,最终的损失函数为三者损失函数(分类损失、重要性损失和负载损失)的加权之和: $$\mathcal{L}_{\mathrm{aux}}(X)=\frac12~\mathcal{L}_{\mathrm{imp}}(X)+\frac12~\mathcal{L}_{\mathrm{load}}(X) \\ \mathcal{L}(X)=\mathcal{L}_{\text{classification}}(X)+\lambda \mathcal{L}_{\text{aux}}(X); \lambda = 0.01$$
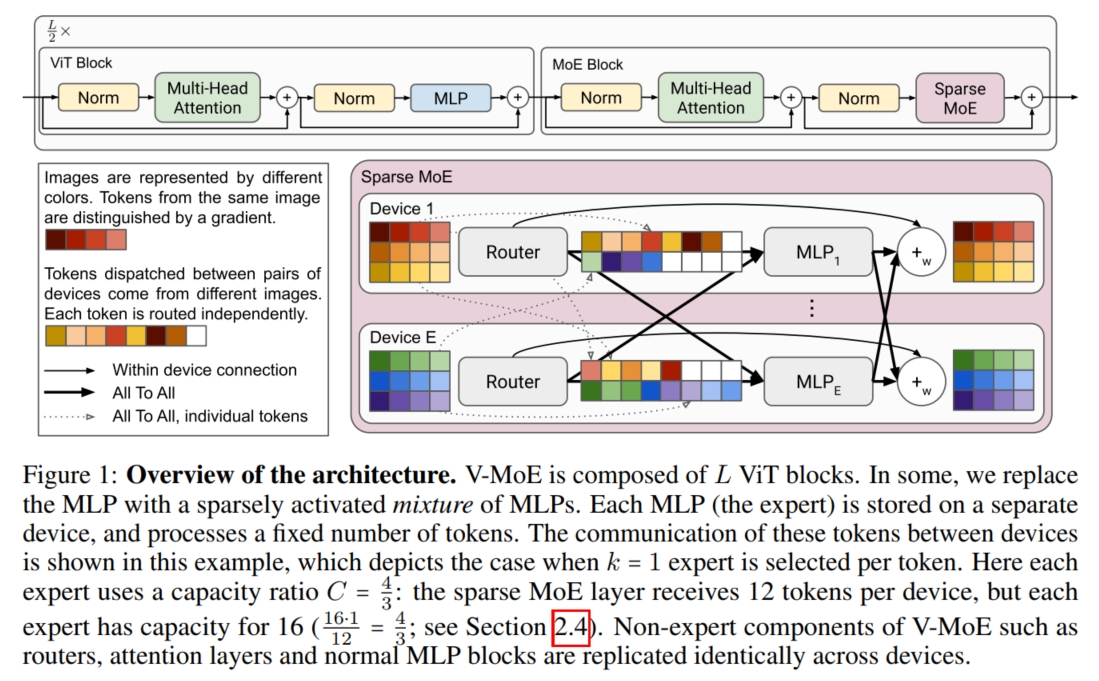

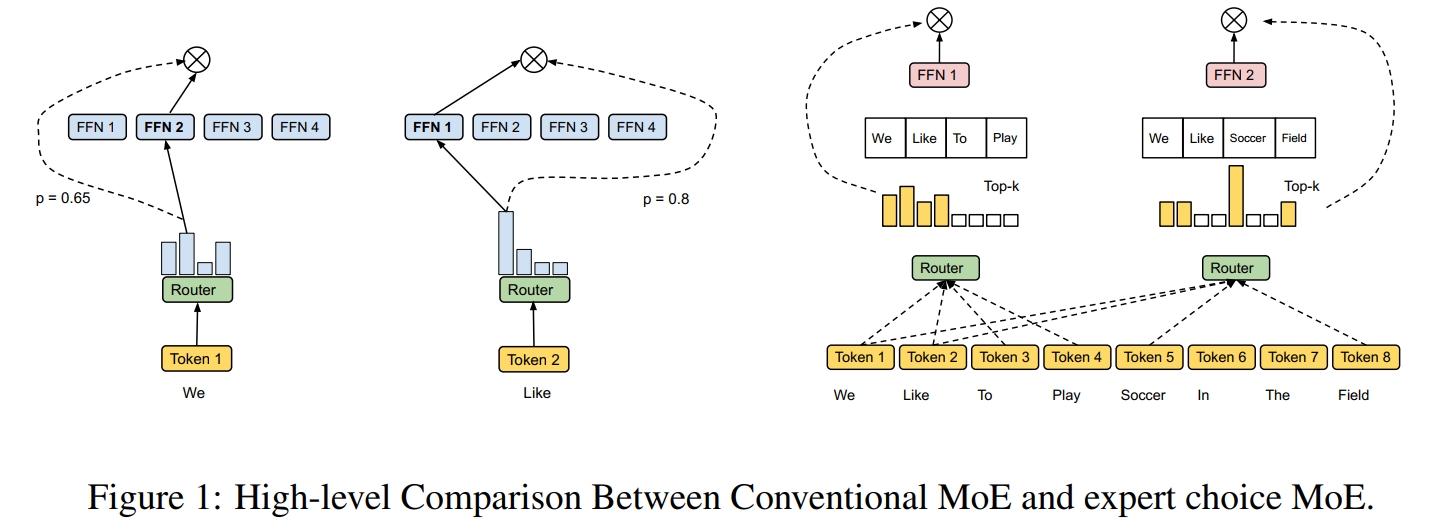
Expert Choice Routing: 先前的 MoE 方法中的 Gating Model 都是针对每一个数据 $x$ 分配固定数量的 expert 模型。 这种方法忽视了数据之间的关联性(因为每个数据都是独立经过 Gating Model 进行 expert 模型选择), 同时会造成计算资源不平衡(即可能导致大多数数据都集中在部分 expert 模型进行学习,而导致其他 expert 模型的空闲)。 因此,Expert Choice Routing 改变了分配策略,显式地平均分配数据至每个 expert 模型,即针对每个 expert 模型分配固定数量的数据 $x$。 具体而言,假设有 $n$ 个 $d$ 维数据 $X \in \mathbb{R}^{n \times d}$,$e$ 个 expert 模型,每个 expert 模型的数据处理容量为 $k$。 首先设置 $k = \dfrac{n \times c}{e}$ (其中 $n$ 表示一个 batch 的总数据量,$c$ 表示容量因子,$e$ 表示 expert 数量), 再计算每个数据分配给各个 expert 模型的权重 $S \in \mathbb{R}^{n \times e}$; 然后根据 $S$ 使用 $\text{ KeepTopK }$ 函数选择每个 expert 模型的前 $k$ 个数据; 最后再使用 $S$ 中对应位置的权重对每个数据进行加权求和得到最终输出 $O \in \mathbb{R}^{n \times d}$。 再具体实现上,可以使用索引矩阵 $I \in \mathbb{R}^{e \times k}$ (其中 $(i,j)$ 位置表示第 $i$ 个 expert 模型选择第 $j$ 个数据), 门控权重矩阵 $G \in \mathbb{R}^{e \times k}$ (其中 $(i,j)$ 位置表示第 $i$ 个 expert 模型选择第 $j$ 个数据的权重) 以及 one-hot 矩阵 $P \in \mathbb{R}^{e \times k \times n}$: $$S=\operatorname{Softmax}\left(X \cdot W_g\right), \quad S \in \mathbb{R}^{n \times e} \\ G, I=\operatorname{TopK}\left(S^{\top}, k\right), P=\operatorname{Onehot}(I)$$ 假设 Transformer 的 FFN 层的参数权重为 $W_1 \in \mathbb{R}^{d \times d'}$ 和 $W_2 \in \mathbb{R}^{d' \times d}$,则其输入输出为: $$X_{in} = P \cdot X \in \mathbb{R}^{e \times k \times d} \\ \forall i = 1 \sim e: X_e[i] = GeLU(X_{in}[i] \cdot W_1[i]) \cdot W_2[i]^T \\ X_{out}[l,d] = \sum_{i,j}P[i,j,l]G[i,j]X_e[i,j,d] \in \mathbb{R}^{n \times d}$$ 其中,$X_e$ 和 $X_{out}$ 可以使用 Einstein summation (einsum) 操作算子计算。 可以看到,Expert Choice Routing 通过显式地为每个 expert 模型分配数据来彻底解决各个 expert 模型的数据处理不均衡问题, 但是这又引入了一个新的问题:其有可能导致部分的数据一直没有被任意一个/只被少量的 expert 模型所处理。 为此,需要限制每个数据分配到的 expert 模型数量。具体而言,假设 $A \in \mathbb{R}^{e \times n}$ 表示选择矩阵,其中 $A[i,j]$ 表示第 $i$ 个模型是否选择处理第 $j$ 个数据。 然后讲上述问题转化为一个熵正则化线性规划问题: $$\underset{A}{max}<S^T, A> + \lambda H(A); H(A) = \sum_{ij}-A[i,j]logA[i,j] \\ s.t. \left \{ \begin{array}{l} \forall i = 1 \sim e: \sum_{j'=1}^{n}A[i,j'] = k; \\ \forall j = 1 \sim n: \sum_{i'=1}^{e}A[i',j] \leq b; \\ \forall i = 1 \sim e, j = 1 \sim n: 0 \leq A[i,j] \leq 1\end{array}\right.$$ 其中,$H(A)$ 是逐元素熵之和,添加一个小的熵项可以提供一个接近整数的解结果, 同时能够使用一个可以在 TPU 上运行的快速迭代求解器;$b > 0$ 是一个正整数表示每个数据分配到的 expert 模型数量的上界(即最大值)。 观察上述式子,可以发现解空间是三个凸集的交集,每个凸集都满足其中一个线性约束,因此可以使用 Dykstra 算法,交替地将中间解投影到一个凸集上来求解 $A$。 在计算出 $A$ 后,再使用 $\operatorname{TopK}(A;k)$ 获得索引矩阵 $I$。
References
Hard Mixtures of Experts for Large Scale Weakly Supervised Vision
Outrageously Large Neural Networks: The Sparsely-Gated Mixture-of-Experts Layer
Switch transformers: scaling to trillion parameter models with simple and efficient sparsity
GLaM: Efficient Scaling of Language Models with Mixture-of-Experts
GShard: Scaling Giant Models with Conditional Computation and Automatic Sharding
Mixture-of-Experts Meets Instruction Tuning:A Winning Combination for Large Language Models
Mixture of Experts: How an Ensemble of AI Models Decide As One - Blog
