这篇博客主要介绍了 Large Language Model 的基础知识，包括常见的 LLM，微调方式等。

Fine-Tuning

微调是指将预训练好的 LLM 模型使用特定任务 $T$ 的数据集进行进一步训练，以进一步提高 LLM 在该任务上的性能。 假设 LLM 模型的预训练参数为 $W/W_0 \in \mathbb{R}^{d \times k}$，微调时的参数更新量为 $\Delta W$。 最简单的微调方式是使用该任务 $T$ 的数据集 $\mathcal{D}_T = \{x_i,y_i\}_{1:N}$ 对 LLM 进行监督训练，则 $\Delta W$ 是通过 BP 算法计算得到，其维度和 $W$ 一致。 这种方式存在 $2$ 个主要问题：

1. 模型微调的资源消耗过大，由于是直接在任务数据集训练整个 LLM 模型，则在每一次 BP 梯度更新时其计算量和内存消耗与模型参数成正比；
2. 模型参数的利用率较低，上述微调方式是直接在原有的预训练模型参数上进行更新，导致每微调一个特定任务 $T_i$ 的 LLM 模型，都必须要保存整个更新后参数的模型， 而每个任务特定的 LLM 模型和原始预训练模型的大小是一致的。

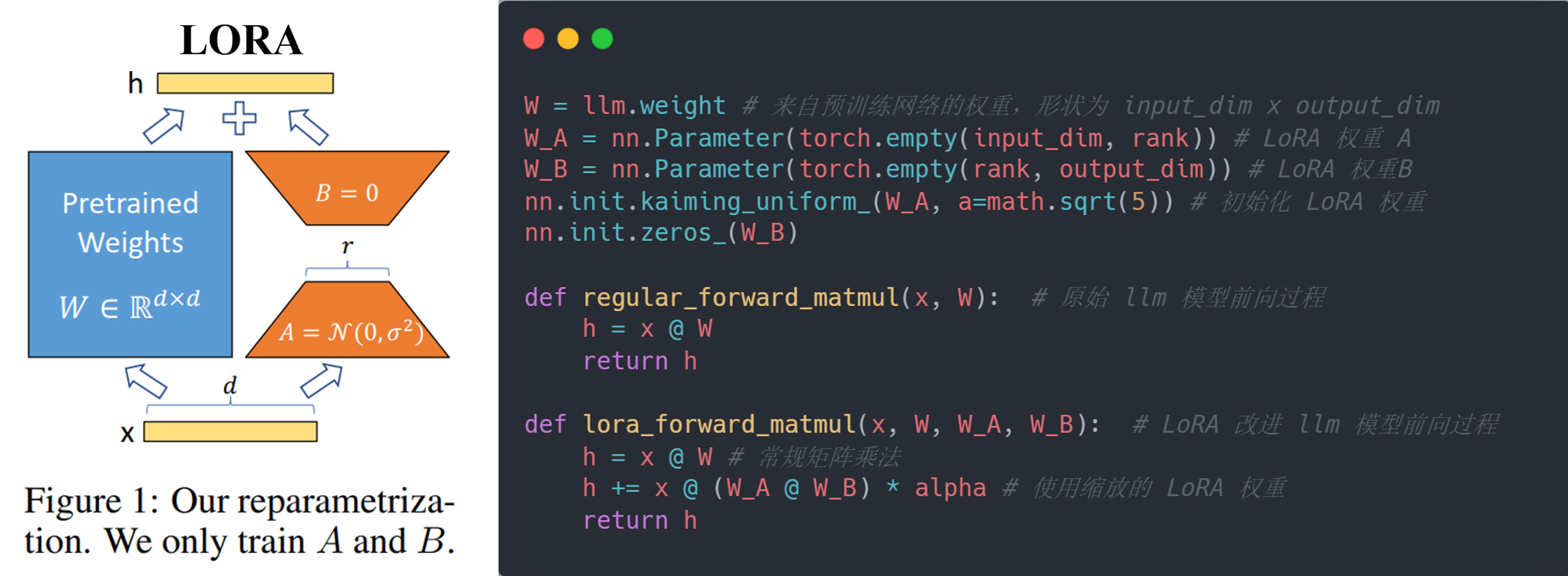
LoRA：Low-Rank Adaptation， 是一种通过显式构造 LLM 模型参数更新来实现微调的方式。它主要通过分离 LLM 模型的参数更新量 $\Delta W$ 以及降低 $\Delta W$ 的维度的方式来优化微调过程。 具体而言，如下图所示，本文将 $\Delta W$ 显式地作为一个可训练的参数来将其与原始预训练参数 $W$ 进行分离。对于 $W$，LoRA 引入一个额外的可训练参数(nn.Parameter) $\Delta W$ 来表示其更新量， 则模型的前向过程(forward)转化为 $h = (W_0 + \Delta W)x = W_0x + \Delta Wx$。 同时，LoRA 假设 LLM 微调时的模型参数更新量 $\Delta W$ 是一个低秩矩阵，即 $Rank(\Delta W) \ll min(d,k)$，则可以通过将其分解为两个低秩矩阵的乘积来降低维度：

因此，$\Delta W$ 转化为 $2$ 个维度更低的可训练参数(nn.Parameter) $B$ 和 $A$，模型的前向过程也转化为 $h = W_0x + BAx$。 在初始化时，可以对 $A$ 使用高斯随机初始化，而将 $B$ 初始化为 $0$，这样在开始时 $\Delta W = BA = 0$，模型保持预训练时的性能。 在模型微调时，LoRA 保持损失函数不变，使用该任务 $T$ 的数据集 $\mathcal{D}_T = \{x_i,y_i\}_{1:N}$ 对改进后的模型进行监督训练，且只训练引入的额外参数 $B$ 和 $A$，相比于训练整个 $W$ 要容易， 并且将 $\Delta W$ 使用 $\dfrac{\alpha}{r}$ 进行缩放，即 $\Delta W = \dfrac{\alpha}{r}BA$，其中 $\alpha$ 是针对 $r$ 的一个常数，但是对于不同的 $r$ 其值不同，这样可以更好地调节模型的微调程度。 而在推理时，可以选择将 $W$ 和更新后的 $\Delta W = BA$ 进行融合形成 $\hat{W} = W_0 + \Delta W$，然后进行一步推理；也可和微调时一样，并行地计算 $W_0x$ 和 $\Delta Wx$，然后进行相加。 同时，对于多个特定任务的微调，每个任务的模型都可以共用 $W$，只需微调和存储各自的 $B$ 和 $A$ 即可。(参考资料)